a) Tìm \(M\) để đồ thị hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\):

Để hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\), ta thay giá trị \(x = 2\) và \(y = 4\) vào phương trình hàm số:

\(y = \left(\right. m + 1 \left.\right) x^{2}\)

Thay \(x = 2\) và \(y = 4\):

\(4 = \left(\right. m + 1 \left.\right) \cdot 2^{2}\) \(4 = \left(\right. m + 1 \left.\right) \cdot 4\) \(4 = 4 \left(\right. m + 1 \left.\right)\)

Chia cả hai vế cho 4:

\(1 = m + 1\) \(m = 0\)

Vậy giá trị của \(m\) là 0.

like minh nhe minh lam duoc cau a thôi

Để giải bài toán này, chúng ta sẽ thực hiện từng bước một.

a) Tìm \(m\) để đồ thị hàm số đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\)

1. Thay tọa độ điểm A vào hàm số:
   Hàm số cho trước là: \(y = \left(\right. m + 1 \left.\right) x^{2}\)Thay \(x = 2\) và \(y = 4\): \(4 = \left(\right. m + 1 \left.\right) \left(\right. 2^{2} \left.\right)\)
2. Giải phương trình:
   Tính giá trị \(2^{2}\): \(2^{2} = 4 \Rightarrow 4 = \left(\right. m + 1 \left.\right) \cdot 4\)Chia cả hai vế cho 4: \(1 = m + 1\)Trừ 1 từ cả hai vế: \(m = 0\)

Kết luận phần a:

• Giá trị của \(m\) là \(0\).

b) Vẽ đồ thị hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) với giá trị \(m\) vừa tìm được

1. Thay giá trị \(m\) vào hàm số:
   Với \(m = 0\): \(y = \left(\right. 0 + 1 \left.\right) x^{2} = x^{2}\)
2. Xác định các điểm trên đồ thị:
3. • Khi \(x = - 2\), \(y = \left(\right. - 2 \left.\right)^{2} = 4\)
   • Khi \(x = - 1\), \(y = \left(\right. - 1 \left.\right)^{2} = 1\)
   • Khi \(x = 0\), \(y = 0^{2} = 0\)
   • Khi \(x = 1\), \(y = 1^{2} = 1\)
   • Khi \(x = 2\), \(y = 2^{2} = 4\)
4. Vẽ đồ thị:
   Đồ thị của hàm số \(y = x^{2}\) là một parabol mở lên trên. Các điểm mà chúng ta đã tính sẽ giúp hình dung đồ thị:
5. • Điểm \(\left(\right. - 2 , 4 \left.\right)\)
   • Điểm \(\left(\right. - 1 , 1 \left.\right)\)
   • Điểm \(\left(\right. 0 , 0 \left.\right)\)
   • Điểm \(\left(\right. 1 , 1 \left.\right)\)
   • Điểm \(\left(\right. 2 , 4 \left.\right)\)

Kết luận phần b:

• Đồ thị của hàm số \(y = x^{2}\) là một parabol mở lên với đỉnh tại điểm \(\left(\right. 0 , 0 \left.\right)\).

Nếu bạn cần thêm thông tin hoặc có câu hỏi gì khác, hãy cho tôi biết!

Duyên đã từng trải qua một tình huống tương tự hoặc nghe kể về những tình huống nguy hiểm khi giúp đỡ người lạ. Điều này khiến cô ấy lo lắng và cố gắng ngăn cản mẹ và anh trai để đảm bảo an toàn cho gia đình mình, nhưng cảm thấy bất lực khi không thể thuyết phục họ ngay lúc đó.

Đoạn thơ trên vẽ nên một bức tranh thiên nhiên mùa đông, nơi mọi vật dường như đang co mình lại để chống chọi với cái lạnh giá. Tuy nhiên, ẩn sâu trong đó là một sức sống tiềm tàng, một niềm hy vọng về sự hồi sinh của mùa xuân.

Hình ảnh "cỏ giấu mầm trong gốc" gợi lên sự ẩn mình, chờ đợi thời cơ. Mầm cỏ tuy nhỏ bé nhưng mang trong mình sức sống mãnh liệt, âm thầm chuẩn bị cho ngày đông qua, xuân đến.

"Lá bàng như giấu lửa" là một so sánh độc đáo, thể hiện sự kiên cường của cây bàng trước cái lạnh. Màu đỏ của lá bàng gợi liên tưởng đến ngọn lửa, nhưng ngọn lửa ấy không bùng cháy mà được "giấu" đi, như một sự tích lũy năng lượng để chờ đợi thời điểm thích hợp.

"Búp gạo như thập thò/Ngại ngần nhìn gió bấc" cho thấy sự e dè, yếu ớt của mầm non trước cơn gió lạnh. Tuy nhiên, dù "ngại ngần", mầm non vẫn "thập thò", vẫn hướng ra ngoài, vẫn khao khát ánh sáng mặt trời.

"Cánh tay soan khô khốc/Tạo dáng vào trời đông" là hình ảnh cây soan khẳng khiu, trơ trụi giữa mùa đông. Dáng vẻ "khô khốc" ấy gợi lên sự khắc nghiệt của thời tiết, nhưng đồng thời cũng thể hiện ý chí kiên cường, không chịu khuất phục của cây soan.

Nhìn chung, đoạn thơ sử dụng nhiều hình ảnh ẩn dụ, so sánh tinh tế để diễn tả một cách sinh động, sâu sắc về sức sống tiềm tàng của thiên nhiên trong mùa đông. Dù phải đối mặt với nhiều khó khăn, thử thách, nhưng mọi vật vẫn luôn ấp ủ trong mình niềm tin về một ngày mai tươi sáng hơn.

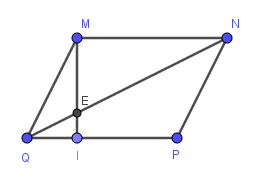
Do \(MNPQ\) là hình bình hành (gt)

\(\Rightarrow MN=PQ\)

Mà \(QI=\dfrac{1}{3}PQ\left(gt\right)\)

\(\Rightarrow QI=\dfrac{1}{3}MN\)

\(\Rightarrow\dfrac{QI}{MN}=\dfrac{1}{3}\)

Do \(MNPQ\) là hình bình hành (gt)

\(\Rightarrow MN\) // \(PQ\)

\(\Rightarrow MN\) // \(QI\)

\(\Rightarrow\dfrac{QI}{MN}=\dfrac{QE}{EN}=\dfrac{1}{3}\)

\(\dfrac{QE}{EN}=\dfrac{1}{3}\Rightarrow EN=3QE\)

Mà \(EN+QE=NQ=18\left(cm\right)\)

\(\Rightarrow3QE+QE=18\)

\(\Rightarrow4QE=18\)

\(\Rightarrow QE=\dfrac{18}{4}=4,5\left(cm\right)\)

🆘🆘🆘

Chọn B nha bạn

ta có:

48

(\(x+1\)) + (\(x+3\))+ ... + (\(x+99\) ) = 3400

Xét dãy số: \(x+1\); \(x+3\); ... ; (\(x+99\))

Dãy số trên là dãy số cách đều với khoảng cách là:

\(x+3\) - \(x\) - 1 = 2

Số số hạng của dãy số trên là:

(\(x+99\) - \(x-1\)) : 2 + 1 = 99 (số)

Tồng của dãy số trên là:

(\(x+99+x+1\)) x 99 : 2 = (\(x\) x 2 + 100) x 99 : 2

Vậy ta có:

(\(x\) x 2 + 100) x 50 : 2 = 3400

(\(x\) x 2 + 100) x 50 = 3400 x 2

(\(x\) x 2 + 100) x 50 = 6800

(\(x\) x 2 + 100) = 6800 : 50

\(x\) x 2 + 100 = 136

\(x\) x 2 = 136 - 100

\(x\) x 2 = 36

\(x=36\) : 2

\(x=18\)

\(\left(x+1\right)+\left(x+3\right)+\left(x+5\right)+...+\left(x+99\right)=3400\)

\(x+x+x+...+x+1+3+5+...+99=3400\) (1)

Số các số hạng của dãy 1; 3; 5; ...; 99:

\(\left(99-1\right):2+1=50\) (số)

\(\left(1\right)\Rightarrow50\times x+\left(99+1\right)\times50:2=3400\)

\(50\times x+2500=3400\)

\(50\times x=3400-2500\)

\(50\times x=900\)

\(x=900:50\)

\(x=18\)

Vậy \(x=18\)

• "Tiếng chim líu lo như những lời thì thầm ngọt ngào của buổi sớm mai."
  → Tiếng chim được nhân hóa như một người thì thầm nhẹ nhàng.
• "Tiếng chim hót vang rộn rã như một bản nhạc vui tươi của mùa xuân."
  → So sánh tiếng chim như một bản nhạc do con người sáng tác.
• "Chim hót ríu rít như những đứa trẻ đang trò chuyện vui vẻ."
  → Nhân hóa tiếng chim thành cuộc trò chuyện giữa trẻ em.
• "Tiếng chim cất lên như giọng hát trong trẻo của một cô bé đang ngân nga."
  → So sánh với giọng hát con người để tạo sự gần gũi.
• "Chim ca líu lo như những nghệ sĩ đường phố đang biểu diễn bản nhạc của riêng mình."
  → Biến chim thành những nghệ sĩ, tạo hình ảnh sinh động.

Tiếng chim hót như một bản nhạc làm xua tan đi những muộn phiền. 🐦