Cho hai tam giác bằng nhau: tam giác DEF (không có hai góc nào hoặc hai cạnh nào bằng nhau) và một tam giác có ba đình G, H, K. Viết kí hiệu về sự bằng nhau của hai tam giác đó biết rằng:
a) EF = GH, ED = GK
c) góc F = góc G , góc D = góc H
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
7 tháng 7 2019
\(a,13.|x|-\frac{16}{3}=\frac{23}{3}\)
\(13.|x|=13\)
TH1:\(13.x=13\)
x=13:13
x=1
TH2:\(13.x=-13\)
x=-13:13
x=-1
\(b,19-\left(|x|+1\right)=18\)
\(|x|+1=1\)
TH1:x+1=1
x=1-1
x=0
TH2:x+1=-1
x=-1+1
x=0
(lạ thật )
\(c,|x|=5-x\)
TH1=>x=5-x
=>x-x=5
=>x=5
TH2:-x=5-x
-x+x=5
Làm theo ý tưởng
7 tháng 7 2019
a, Lời giải
TH1 : 13.x=13
x=13:13
x=1
13.x=-13
x=-13:13
x=-1
mấy câu kia tương tự
7 tháng 7 2019
a) |x| = 0
<=> x = 0
b) |x| bé hơn hoặc bằng 3 và x thuộc Z
<=> x \(\in\){\(0;\pm1;\pm2;\pm3\)}
c) |x| = 4 và x > 0
<=> x = 4
d) | - x | = | - 2 |
<=> x = \(\pm2\)
e) |-x| = 1 va x > 0
<=> x = 1
f) |-x| = 0
<=> x = 0
g) |x| = | -3 |
<=> x = \(\pm3\)
Mình làm hết luôn r nha
h) |-x| = |-2|
7 tháng 7 2019
\(a,\frac{1}{3}x+\frac{2}{5}\left(x-1\right)=0\)
\(\frac{\Rightarrow1}{3}x+\frac{2}{5}x-\frac{2}{5}=0\)
\(\Rightarrow x\left(\frac{1}{3}+\frac{2}{5}\right)=\frac{2}{5}\)
\(\frac{\Rightarrow11}{15}x=\frac{2}{5}\)
\(\Rightarrow x=\frac{2}{5}:\frac{11}{15}\)
\(\Rightarrow x=\frac{6}{11}\)
7 tháng 7 2019
\(b,\frac{1}{3}+\frac{2}{3}:x=-7\)
\(\frac{2}{3}:x=-7-\frac{1}{3}\)
\(\frac{2}{3}:x=-\frac{22}{3}\)
\(x=\frac{2}{3}:\left(-\frac{22}{3}\right)\)
\(x=-\frac{1}{11}\)
\(\text{Vậy }x=-\frac{1}{11}\)
KN
1
7 tháng 7 2019
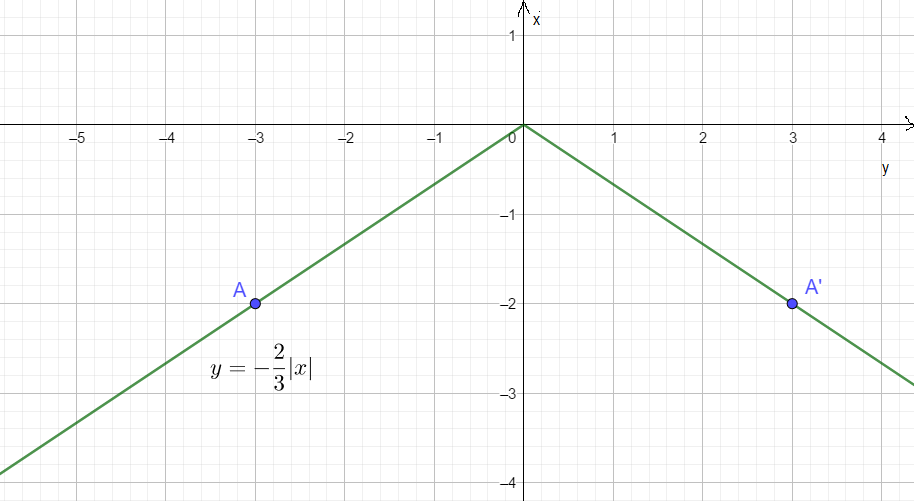
Ta có hàm số: \(y=-\frac{2}{3}|x|\)
Với \(x\ge0\), ta có hàm số \(y=-\frac{2}{3}.x\) . Đồ thị hàm số này là một đường thẳng qua gốc tọa độ.
Với \(x< 0\), ta có hàm số \(y=\frac{2}{3}.x\). Đồ thị hàm số này là một đường thẳng qua gốc tọa độ.
Ta có bảng giá trị:
| x | -3 | 0 | 3 |
| y = f(x) | -2 | 0 | -2 |
Ta có đồ thị hàm số:
KN
4
7 tháng 7 2019
\(S=\frac{3^{1-1}+1}{2}+\frac{3^{2-1}+1}{2}+\frac{3^{3-1}+1}{2}+...+\frac{3^{n-1}+1}{2}\)
\(S=\frac{\left(3^0+3^1+3^2+...+3^{n-1}\right)+\left(1+1+1+...+1\right)}{2}\)có n c/s 1
\(S=\frac{\frac{\left(3^n-1\right)}{2}+n}{2}\)
\(=3^n-1+\frac{n}{2}\)
...\(3^0+3^1+3^3+...+3^{n-1}\)bạn tính nha
KN
7 tháng 7 2019
Câu hỏi của WINNER - Toán lớp 7 - Học toán với OnlineMath
๖ۣۜƝƘ☆ŤŔầŃ➻❥VăŃ➻❥ŃÁM❖︵copy ở đây
7 tháng 7 2019
a)\(\frac{-15}{18}-\left(x-\frac{1}{3}\right)=\frac{25}{27}\)
\(\frac{-5}{6}-x+\frac{2}{6}=\frac{25}{27}\)
\(\frac{-1}{2}-x=\frac{25}{27}\)
\(x=\frac{-77}{54}\)
Vậy............
b) \(\frac{-3}{5}-\left(2x-\frac{1}{20}\right)=\frac{3}{4}\)
\(\frac{-12}{20}-2x+\frac{1}{20}=\frac{15}{20}\)
\(\frac{-11}{20}-2x=\frac{15}{20}\)
\(2x=\frac{-13}{10}\)
\(x=\frac{-13}{20}\)
Vậy.............
8 tháng 7 2019
1.
\(a,-\frac{15}{18}-\left(x-\frac{1}{3}\right)=\frac{25}{27}\)
\(-\frac{5}{6}-x+\frac{2}{6}=\frac{25}{27}\)
\(-\frac{1}{2}-x=\frac{25}{27}\)
\(x=-\frac{77}{54}\)
\(b,-\frac{3}{5}-\left(2x-\frac{1}{20}\right)=\frac{3}{4}\)
\(-\frac{12}{20}-2x+\frac{1}{20}=\frac{15}{20}\)
\(-\frac{11}{20}-2x=\frac{15}{20}\)
\(2x=-\frac{13}{10}\)
\(x=-\frac{13}{20}\)
2.
\(a,-\frac{5}{6}\)và \(1,2\)
\(=-\frac{5}{6}\)và \(\frac{12}{10}\)
\(=-\frac{50}{60}\)và \(\frac{72}{60}\)
Nếu như quy đồng 2 số lên thì ta đc \(-\frac{50}{60}< \frac{72}{60}\)
\(\Rightarrow-\frac{5}{6}\)\(< 1,2\)
\(b,\frac{15}{16}\)và \(\frac{17}{18}\)
Theo như những bài toán đã hc thìn ội dung ở cuối bài là phân số nào có tử bé hơn thì có phân số lớn hơn phân số có tử lớn hơn
\(\Rightarrow\frac{15}{16}>\frac{17}{18}\)
\(c,\frac{1999}{2000}\)và \(\frac{2000}{2001}\)
Ta quy đồng
Đc
\(\frac{3999999}{4002000}\)và \(\frac{4000000}{4002000}\)
\(\Rightarrow\frac{1999}{2000}< \frac{2000}{2001}\)