
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 4,5 x 5,3 + 4,7 x 4,5
= 4,5 x (5,3 + 4,7)
= 4,5 x 10
= 45
b) 73,5 x 35,64 - 73,5 x 64,37
= 73,5 x (35,64 - 64,37)
= 73,5 x -28,73
= -2111,655
c)
\(\dfrac{2007\times2006-8}{2005\times2007+1999}\\ =\dfrac{2007\times\left(2005+1\right)-8}{2007\times2005+1999}\\ =\dfrac{2007\times2005+2007-8}{2007\times2005+1999}\\ =\dfrac{2007\times2005+1999}{2007\times2005+1999}\\ =1\)
a) \(4,5\times5,3+4,7\times4,5\)
\(=4,5\times\left(5,3+4,7\right)\)
\(=4,5\times10\)
\(=45\)
b) Sửa đề: \(73,5\times35,63+73,5\times64,37\)
\(=73,5\times\left(35,63+64,37\right)\)
\(=73,5\times100\)
\(=7350\)
c) Sửa đề: \(\dfrac{2007\times2006-8}{2005\times2007+1999}\)
\(=\dfrac{2007\times2005+2007-8}{2007\times2005+1999}\)
\(=\dfrac{2007\times2005+1999}{2007\times2005+1999}\)
\(=1\)

Câu 25:
\(0< \alpha< \dfrac{\Omega}{2}\)
=>\(0< sin\alpha< 1;0< cos\alpha< 1\)
\(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\)
\(=\dfrac{1+sin\alpha+1-sin\alpha}{cos\alpha}=\dfrac{2}{cos\alpha}\)
Câu 28:



a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CH\cdot CB=CA^2\)
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
c: ΔCHA~ΔCAB
=>\(\dfrac{CA}{CB}=\dfrac{AH}{AB}\)
=>\(AB\cdot AC=AH\cdot BC\)
d: \(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{AB^2+AC^2}{AB^2\cdot AC^2}=\dfrac{BC^2}{BH\cdot BC\cdot CH\cdot BC}=\dfrac{1}{BH\cdot CH}=\dfrac{1}{AH^2}\)
a, Xét tam giác AHB và tam giác CAB có
^AHB = ^CAB ; ^ABH _ chung
Vậy tam giác AHB ~ tam giác CAB (g.g)
\(\dfrac{AB}{BC}=\dfrac{HB}{AB}\Rightarrow AB^2=HB.BC\)
tương tự tam giác AHC ~ tam giác CAB
\(\dfrac{AH}{AC}=\dfrac{AC}{BC}\Rightarrow AC^2=AH.BC\)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA ; ^ABH = ^CAH ( cùng phụ với ^BAH )
Vậy tam giác AHB ~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=HB.HC\)
c, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)
d, Ta có \(AH^2=BH.CH\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{BH.CH}=\dfrac{BC^2}{AB^2.AC^2}=\dfrac{AB^2+AC^2}{AB^2.AC^2}=\dfrac{1}{AC^2}+\dfrac{1}{AB^2}\)

1.
a) các y ta có các giá trị công tác là: 1, 2, 3, 4, 5, 6, 7
Tần số của các giá trị là:
Số năm công tác:
1 có 6 y tá
2 có 5 y tá
3 có 5 y tá
4 có 7 y tá
5 có 9 y tá
6 có 5 y tá
7 có 2 y tá
b) Phòng khám có tổng số:
6 + 5 + 5 + 7 + 9 + 5 + 2 = 39 (y tá)
c) Số y tá đã công tác ở phòng khám ít nhất 3 năm là:
5 + 7 + 9 + 5 + 2 = 28 (y tá)


\(15-25\cdot8:\left(100\cdot2\right)\)
\(=15-\dfrac{200}{200}\)
=15-1
=14

Tổng số gà vịt còn sau khi bán là:
145 - 13 - 22 = 110 (con)
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số gà còn lại sau khi bán là:
110 : 5 x 2 = 44 (con)
Số gà ban đầu bác Năm có là:
44 + 13 = 57 (con)
Số vịt ban đầu là:
145 - 57 = 88 (con)
ĐS: ...
Tổng số gà vịt còn lại là:
145-13-22=110(con)
Số gà còn lại là \(110\times\dfrac{2}{3+2}=110\times\dfrac{2}{5}=44\left(con\right)\)
Số gà ban đầu là 44+13=57(con)
Số vịt ban đầu là 145-57=88(con)

a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)
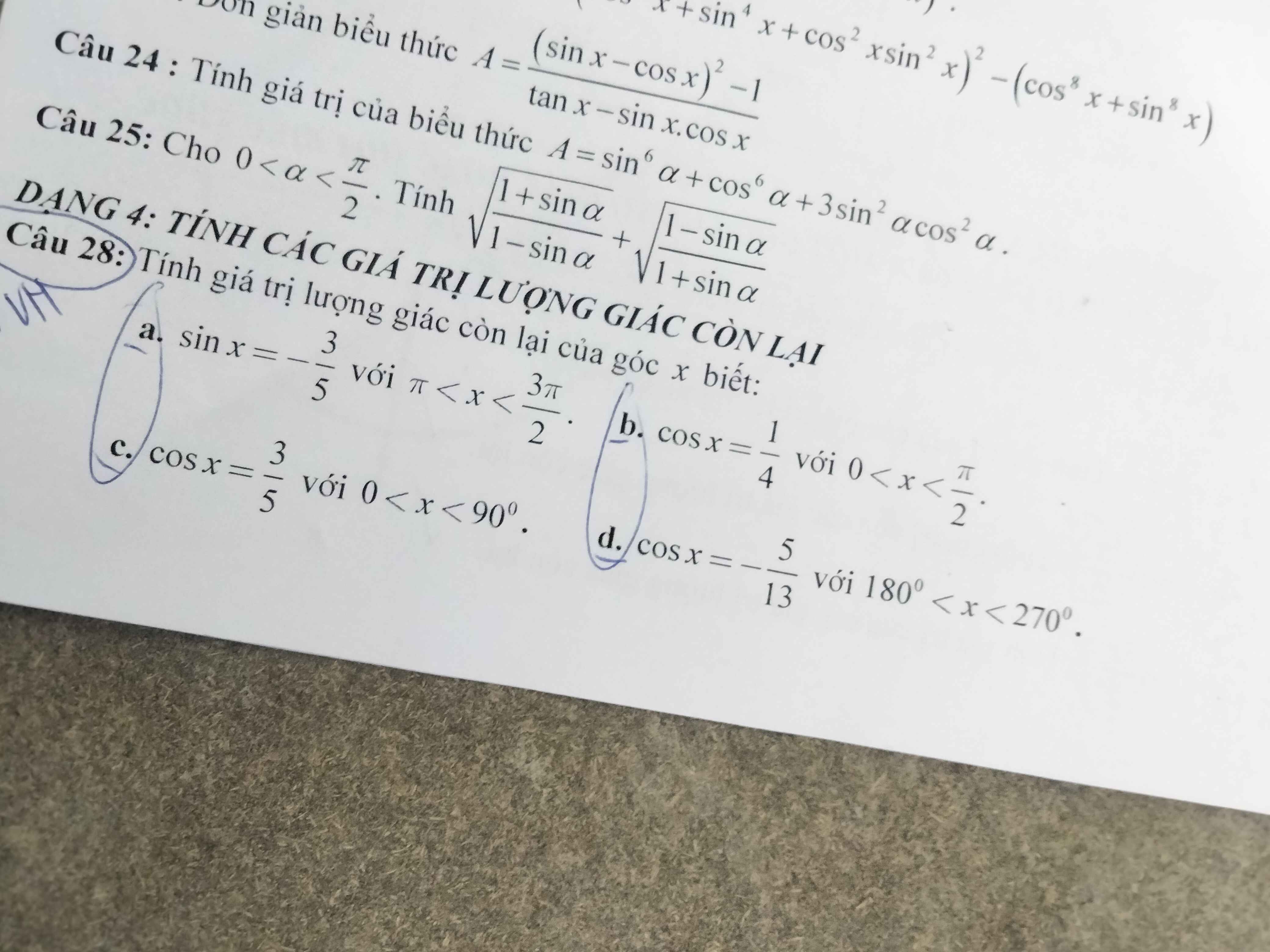
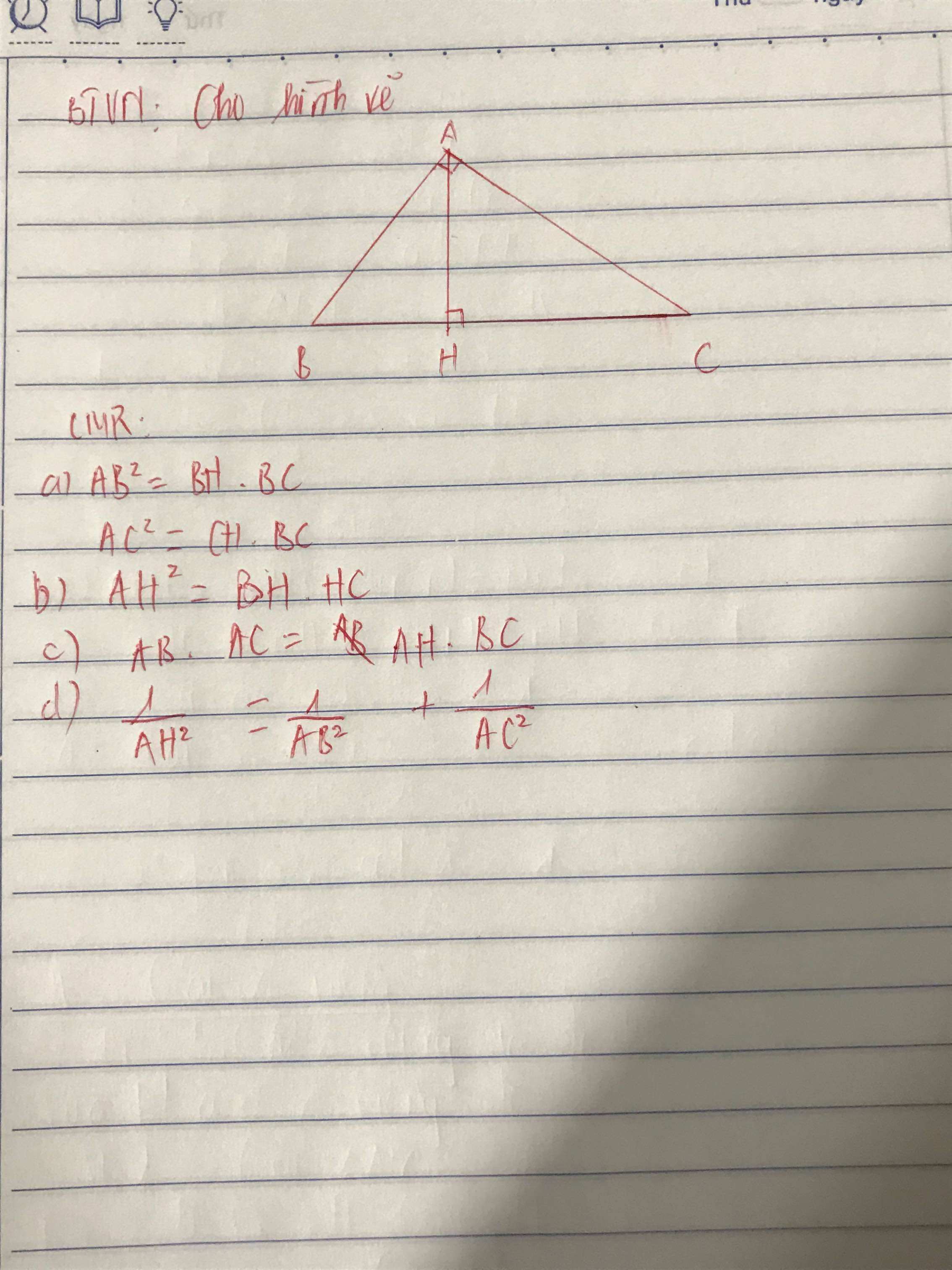


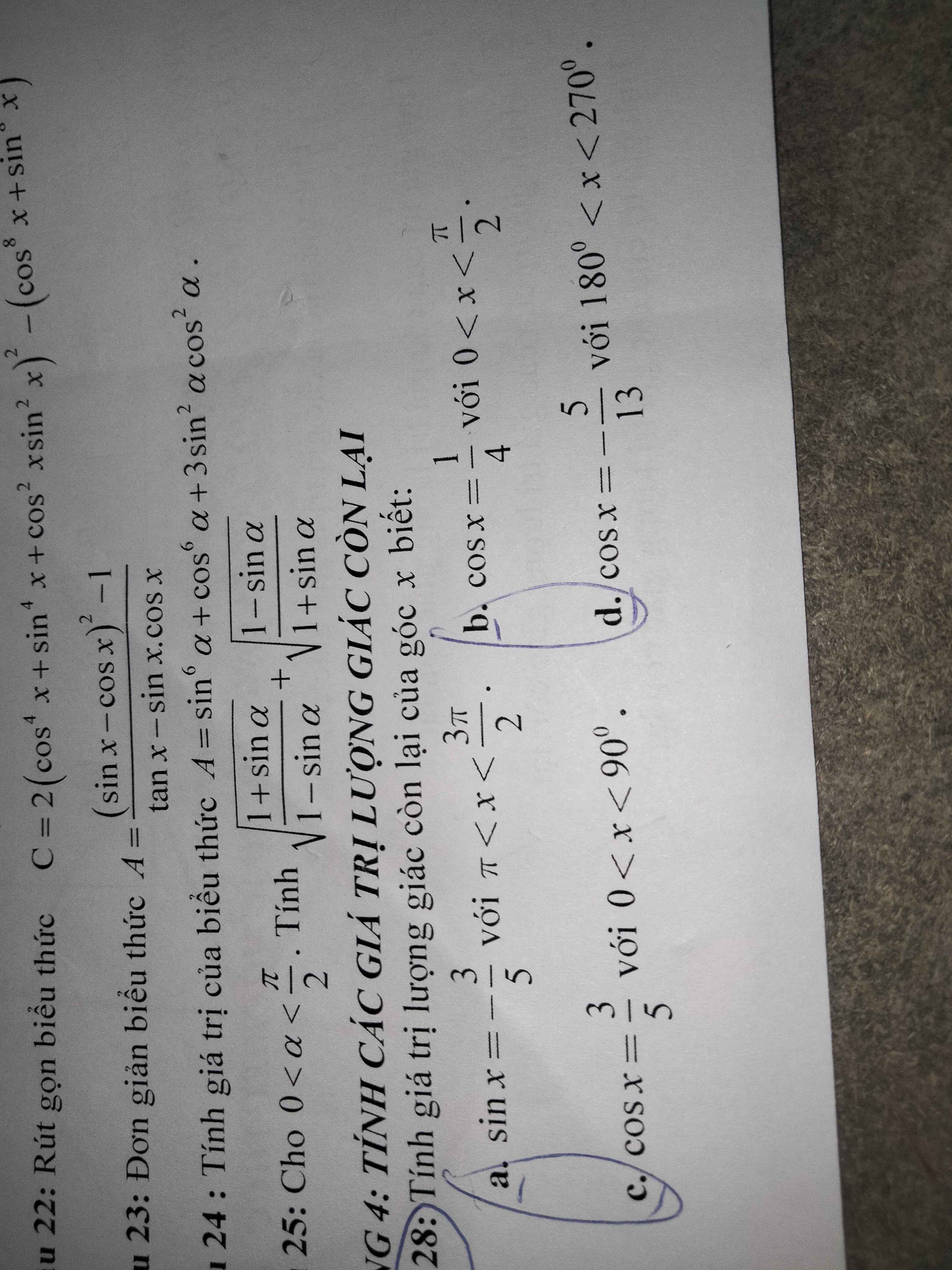
Gọi vận tốc xe tải là: `x` (km/h)
ĐK: x>0
Khi đó vận tốc của xe khách là: `x+15`(km/h)
Lúc xe tải xuất phát thì khoảng cách giữa 2 xe lúc đó là: \(170-\dfrac{5}{3}\left(x+15\right)=170-\dfrac{5}{3}x-25=145-\dfrac{5}{3}x\left(km\right)\)
Lúc gặp nhau thì xe tải đã đi đc: \(\dfrac{2}{3}x\left(km\right)\)
Lúc gặp nhau thì xe khách đã đi thêm đc: \(\dfrac{2}{3}\left(x+15\right)\left(km\right)\)
Ta có pt:
\(\dfrac{2}{3}x+\dfrac{2}{3}\left(x+15\right)=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{2}{3}x+\dfrac{2}{3}x+10=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{4}{3}x+10=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{4}{3}x+\dfrac{5}{3}x=145-10\\ \Leftrightarrow3x=135\\ \Leftrightarrow x=\dfrac{135}{3}=45\left(tm\right)\)
Vận tốc xe khách là 45 + 15 = 60 (km/h)
Gọi vận tốc xe khách, xe tải lần lượt là a ;b ( a;b>0)
xe khách đi nhanh hơn xe tải 15 km/h => a = b + 15
xe khách đi được 5/3 giờ, xe tải bắt đầu xuất phát 2/3 giờ thì gặp nhau
\(\dfrac{7}{3}a+\dfrac{2}{3}b=170\)
\(\left\{{}\begin{matrix}a-b=15\\\dfrac{7}{3}a+\dfrac{2}{3}b=170\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=60\\b=45\end{matrix}\right.\)km/h