Có hai ngọn núi sinh cùng ngày, cùng tháng trong hai năm liên tiếp.Biết tổng số tuổi của hai ngọn núi là 300 501 tuổi.Tính số tuổi của mỗi ngọn núi.
GIÚP MÌNH VỚI,MÌNH ĐANG CẦN GẤP!!!!!!!!!!!!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(22\cdot321+22\cdot456+11\cdot446\)
\(=22\cdot\left(321+456\right)+22\cdot223\)
\(=22\cdot777+22\cdot223=22\cdot1000=22000\)

Bài 2:
a:
Dãy số có quy luật là \(u_n=3\left(n-1\right)+1\left(n\in N\right)\)
Số hạng thứ 100 của dãy là \(u_{100}=3\cdot\left(100-1\right)+1=298\)
b: Tổng của 100 số hạng đó là:
\(\left(298+1\right)\cdot\dfrac{100}{2}=299\cdot50=14950\)
c: \(\dfrac{2025}{3}=675\)
=>2025 không thuộc dãy trên
Bài 1:
a: Dãy số này có quy luật là \(u_n=2n\)
Số hạng thứ 200 là \(2\cdot200=400\)
b: Tổng của 200 số là: \(\left(400+2\right)\cdot\dfrac{200}{2}=402\cdot100=40200\)

\(x\left(x-5\right)+3\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)
Vậy tập nghiệm pt là: \(S=\left\{5;-3\right\}\)
x(x-5)+3(x-5)=0
=>(x-5)(x+3)=0
=>\(\left[{}\begin{matrix}x-5=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)

a: \(\dfrac{1}{4003}>0;0>-\dfrac{75}{106}\)
Do đó: \(\dfrac{1}{4003}>-\dfrac{75}{106}\)
b: \(-19< -17\)
=>\(-\dfrac{19}{31}< -\dfrac{17}{31}\)
c: \(\dfrac{-33}{37}>\dfrac{-34}{37}\)
mà \(-\dfrac{34}{37}>-\dfrac{34}{35}\)
nên \(\dfrac{-33}{37}>-\dfrac{34}{35}\)
d: \(\dfrac{-13}{77}=\dfrac{-13\cdot205}{77\cdot205}=\dfrac{-2665}{77\cdot205}\)
\(\dfrac{-34}{205}=\dfrac{-34\cdot77}{205\cdot77}=\dfrac{-2618}{205\cdot77}\)
mà -2665<-2618
nên \(\dfrac{-13}{77}< \dfrac{-34}{205}\)
e: \(\dfrac{-456}{461}=-1+\dfrac{5}{461};\dfrac{-123}{128}=-1+\dfrac{5}{128}\)
461>128
=>\(\dfrac{5}{461}< \dfrac{5}{128}\)
=>\(\dfrac{5}{461}-1< \dfrac{5}{128}-1\)
=>\(\dfrac{-456}{461}< \dfrac{-123}{128}\)

\(2x^3+10x^2=0\)
=>\(2x^2\left(x+5\right)=0\)
=>\(x^2\left(x+5\right)=0\)(Vì 2>0)
=>\(\left[{}\begin{matrix}x^2=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(2x^3+10x^2=0\Leftrightarrow x^2\left(2x+10\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

15 x 8 + 6 x15 - 15 x 4
= 15 x (8 + 6 - 4)
= 15 x (14 - 4)
= 15 x 10
= 150

`x^2-6x=0`
`<=>x(x-6)=0`
TH1: `x =0 `
TH2: `x - 6=0<=>x=6`
Vậy: ...
\(x^2-6x=0\Leftrightarrow x\left(x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

a: A={x∈N|x=3k+1; k∈N; 0<=k<=6}
b: B={x∈N|x=k3; 1<=k<=5}

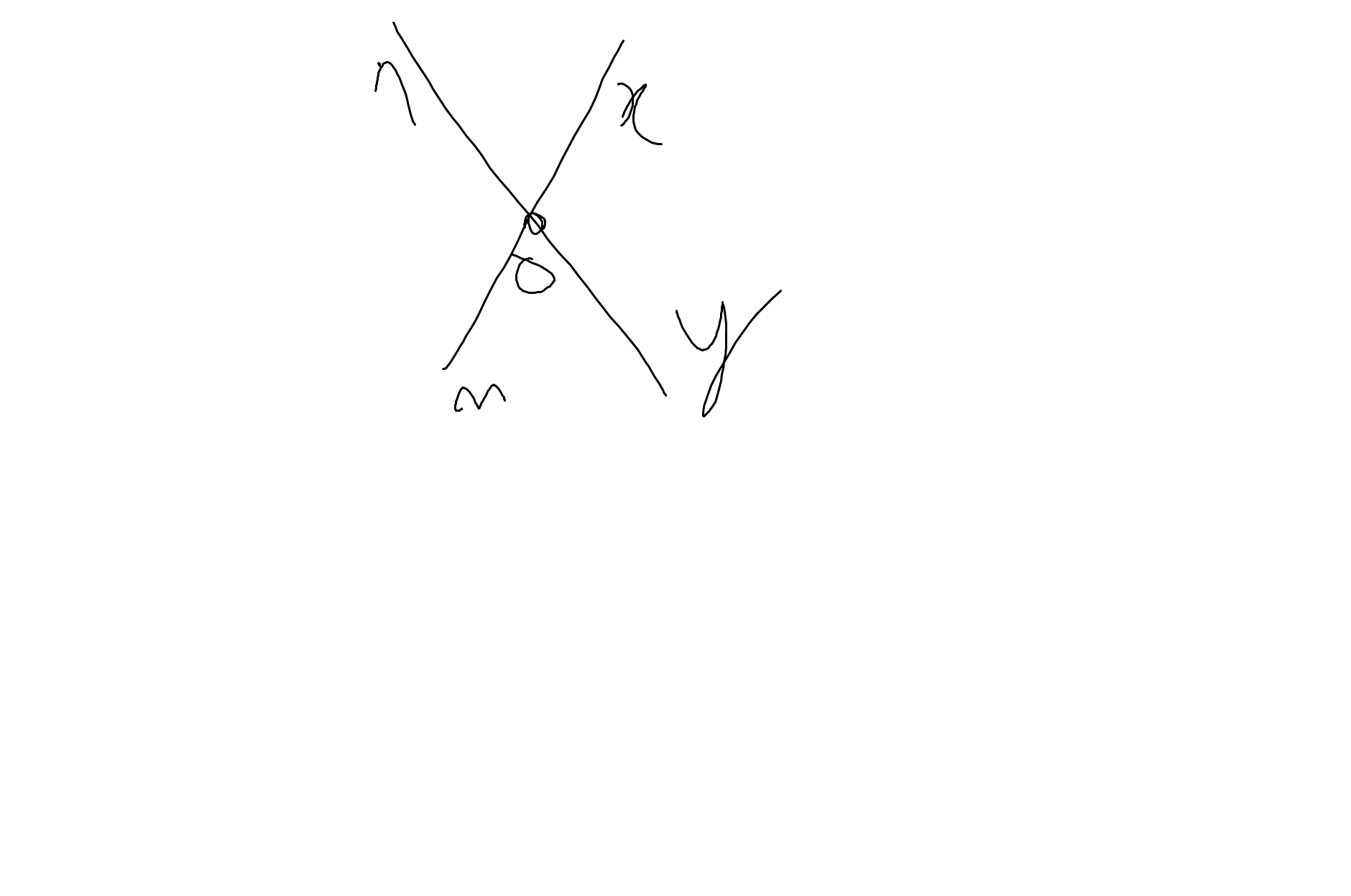
\(\widehat{mOn}=\widehat{xOy}\)(hai góc đối đỉnh)
mà \(\widehat{xOy}=85^0\)
nên \(\widehat{mOn}=85^0\)
Ta có: \(\widehat{nOm}+\widehat{xOn}=180^0\)(hai góc kề bù)
=>\(\widehat{xOn}+85^0=180^0\)
=>\(\widehat{xOn}=180^0-85^0=95^0\)
Ta có: \(\widehat{xOn}=\widehat{yOm}\)(hai góc đối đỉnh)
mà \(\widehat{xOn}=95^0\)
nên \(\widehat{yOm}=95^0\)
Số tuổi của ngọn núi thứ nhất là: (300 501 - 1) : 2 = 150 250 (tuổi)
Số tuổi của ngọn núi thứ 2 là: (300 501 + 1) : 2 = 150 251 (tuổi)
Đáp số: 150 250 tuổi và 150 251 tuổi
.