Bài 2 Chứng minh rằng đường thẳng y =(m-1)x + 2m + 2 l;uôn đi qua điểm P(-2;4) với mọi giá trị của m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
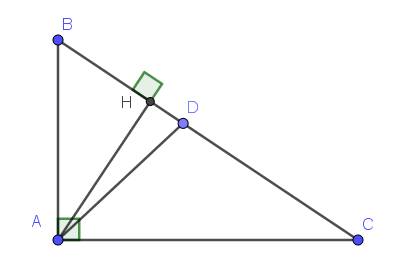
a. Áp dụng định lý Pitago ta có: $BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
Theo tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}$
Mà $BD+DC=BC=5$
$\Rightarrow BD=5:(3+4).3=\frac{15}{7}$ (cm); $DC=5:(3+4).4=\frac{20}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=AB.AC:BC=3.4:5=\frac{12}{5}=2,4$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$HD=BD-BH=\frac{15}{7}-1,8=\frac{12}{35}$ (cm)
$AD=\sqrt{AH^2+HD^2}=\sqrt{2,4^2+(\frac{12}{35})^2}=2,42$ (cm)

ĐKXĐ: \(\left|x-2\right|-1\ne0\)
\(\Rightarrow\left|x-2\right|\ne1\)
\(\Rightarrow\left\{{}\begin{matrix}x-2\ne1\\x-2\ne-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne3\\x\ne1\end{matrix}\right.\)

\(A-B=35^2+33^2+31^2+....+3^2+1^2-\left(34^2+32^2+30^2+....+4^2+2^2\right)\\ =\left(35^2-34^2\right)+\left(33^2-32^2\right)+\left(31^2-30^2\right)+...+\left(3^2-2^2\right)+1^2\\ =\left(35-34\right)\left(35+34\right)+\left(33-32\right)\left(33+32\right)+\left(31-30\right)\left(31+30\right)+....+\left(3-2\right)\left(3+2\right)+1\\ =1.\left(35+34\right)+1.\left(33+32\right)+1.\left(31+30\right)+....+1.\left(3+2\right)+1\\ =1+2+3+....+30+31+32+33+34+35\\ =\dfrac{\left(1+35\right).35}{2}=630\)


Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
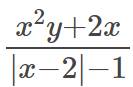
Vì đường thẳng `(d)` luôn đi qua điểm `P(-2;4) =>x=-2;y=4`
Ta có:
`(m-1).(-2)+2m+2=4`
`<=>-2m+2+2m+2-4=0`
`<=>0m=0` (luôn đúng)
Vậy đường thẳng `(d)` luôn đi qua điểm `P(-2;4)` với mọi giá trị của `m`.
tôi học hơi bị giỏi đấy