được

\(\dfrac{1}{2}\)\(x^2\) = \(\dfrac{1}{4}x^2\) + \(\dfrac{1}{4}\)\(x^2\)

a: 2x-3=x+1/2

=>\(2x-x=3+\dfrac{1}{2}\)

=>\(x=\dfrac{7}{2}\)

b: \(4x-\left(2x+1\right)=3-\dfrac{1}{3}+x\)

=>\(4x-2x-1=x+\dfrac{8}{3}\)

=>\(2x-1=x+\dfrac{8}{3}\)

=>\(2x-x=\dfrac{8}{3}+1\)

=>\(x=\dfrac{11}{3}\)

\(\dfrac{15}{23}-\dfrac{21}{23}-\left(-\dfrac{8}{23}\right)-\left(-\dfrac{21}{33}\right)\)

\(=\left(\dfrac{15}{23}+\dfrac{8}{23}-\dfrac{21}{23}\right)+\dfrac{21}{33}\)

\(=\dfrac{2}{23}+\dfrac{21}{33}=\dfrac{2\cdot33+21\cdot23}{23\cdot33}=\dfrac{549}{759}\)

Sửa đề: 

\(\dfrac{15}{23}-\dfrac{21}{23}-\left(-\dfrac{8}{23}\right)-\left(-\dfrac{21}{23}\right)\\ =\dfrac{15}{23}-\dfrac{21}{23}+\dfrac{8}{23}+\dfrac{21}{23}\\ =\left(\dfrac{15}{23}+\dfrac{8}{23}\right)+\left(-\dfrac{21}{23}+\dfrac{21}{23}\right)\\ =1+0\\ =1\)

Ta có: \(\left\{{}\begin{matrix}\left|x+1\right|\ge0\\\left(y-2\right)^{2028}\ge0\end{matrix}\right.\) 

=> \(\left|x+1\right|+\left(y-2\right)^{2028}\ge0\)

Dấu = xảy ra khi: 

\(\left\{{}\begin{matrix}x+1=0\\y-2=0\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
Khi đó: 

`A =` \(x^{2024}+\left(5-y\right)^3\)

`=` \(\left(-1\right)^{2024}\) `+ (5-2)^3 `

`= 1 + 3^3 `

`=1 + 27`

`= 28`

Vậy `A = 28`

giúp mình với mình dg vội

\(a,\left(\dfrac{2}{3}\right)^{x+2}=\dfrac{8}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+2}=\left(\dfrac{2}{3}\right)^3\\ =>x+2=3\\ =>x=3-2\\ =>x=1\\ b,\left(\dfrac{1}{2}\right)^{x+1}=\dfrac{1}{8}\\ =>\left(\dfrac{1}{2}\right)^{x+1}=\left(\dfrac{1}{2}\right)^3\\ =>x+1=3\\ =>x=3-1\\ =>x=2\)

\(\left(12\dfrac{1}{3}-10\dfrac{1}{4}\right):\left(2\dfrac{1}{2}+1\dfrac{1}{3}\right)\\ =\left(\dfrac{37}{3}-\dfrac{41}{4}\right):\left(\dfrac{5}{2}+\dfrac{4}{3}\right)\\ =\dfrac{25}{12}:\dfrac{23}{6}\\ =\dfrac{25}{12}\cdot\dfrac{6}{23}\\ =\dfrac{25}{46}\)

Số m vải còn lại sau khi bán ngày 1 chiếm:

1 - 3/5 = 2/5

Số m vải còn lại sau khi bán ngày 2 chiếm:

2/5 - 2/5 . 2/7 = 2/7

Số mét vải cửa hàng đã bán:

40 : 2/7 = 140 (m)

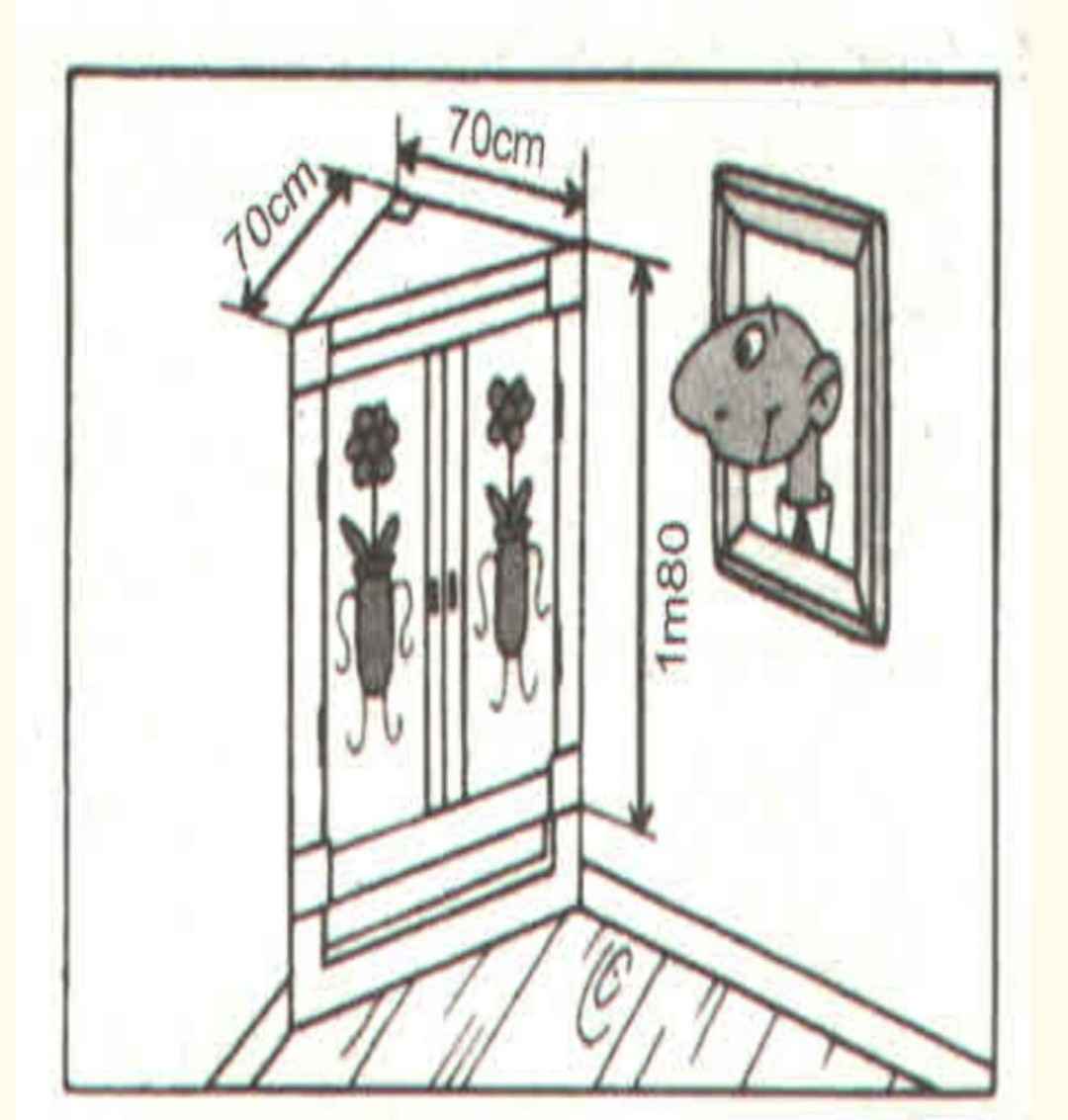
Độ dài cạnh đáy thứ ba của cái tủ là:

\(\sqrt{70^2+70^2}=70\sqrt{2}\left(cm\right)\)

Chu vi đáy của cái tủ là:

\(70+70+70\sqrt{2}=140+70\sqrt{2}\left(cm\right)\)

Diện tích xung quanh của của tủ là:

\(180\cdot\left(140+70\sqrt{2}\right)=25200+12600\sqrt{2}\left(cm^2\right)\)

Diện tích đáy của cái tủ là:

\(\dfrac{1}{2}\cdot70\cdot70=2450\left(cm^2\right)\)

Diện tích toàn phần của cái tủ là:

\(2\cdot2450+\left(25200+12600\sqrt{2}\right)=30100+12600\sqrt{2}\left(cm^2\right)\)