Tìm lim \(\frac{1}{3\cdot4}\)+ \(\frac{1}{4\cdot5}\)+....+\(\frac{1}{n\left(n+1\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

NT
1

24 tháng 3 2020
\(1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n\left(n+1\right)}=1+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\)
\(=2-\frac{1}{n+1}\)
=> \(lim\left(1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n\left(n+1\right)}\right)=lim\left(2-\frac{1}{n+1}\right)=2\)( khi n tiến tới vô cùng )
NT
1

20 tháng 3 2020
to have a lot of influence only over a small area
có nhiều ảnh hưởng trên một khu vực nhỏ nhé
bạn có thể tra trên cambridge dictionary
KD
0


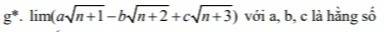
lim\(\left(\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{n\left(n+1\right)}\right)\)
= lim \(\left(\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{n}-\frac{1}{n+1}\right)\)
= lim \(\left(\frac{1}{3}-\frac{1}{n+1}\right)\)
= 1/3
\(\text{GIẢI :}\)
\(lim\left(\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{\text{n}\left(\text{n}+1\right)}\right)\)
\(=lim\left(\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{\text{n}}-\frac{1}{\text{n}+1}\right)\)
\(=lim\left(\frac{1}{3}-\frac{1}{\text{n}\left(\text{n + 1}\right)}\right)\)
\(=\frac{1}{3}\)