a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

ΔABC~ΔHBA

=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}\)

=>\(AH=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7,2\left(cm\right)\)

c: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{9}=\dfrac{DC}{12}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=15cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{15}{7}\)

=>\(DB=\dfrac{45}{7}\left(cm\right);DC=\dfrac{60}{7}\left(cm\right)\)

Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của tam giác vuông và tam giác đồng dạng.

a) Chứng minh tam giác ABC đồng dạng với tam giác HBA; AB^2=BC*HB

Trong tam giác vuông ���ABC, ta có:

• ��=9 cmAB=9cm
• ��=12 cmAC=12cm

Theo định lý Pythagoras, ta có ��=��2−��2=122−92=144−81=63BC=AC2−AB2​=122−92​=144−81​=63​.

Từ đó, ta có: ��2=92=81AB2=92=81 ��=63BC=63​

Trong tam giác vuông ���ABC, đường cao ��AH là đường trung tuyến của tam giác vuông ���ABH, vì ��AH chia ��BC thành hai phần bằng nhau.

Vì vậy, ta có ��=��/2=63/2HB=BC/2=63​/2.

Tam giác ���ABC và ���HBA có góc vuông tại �A và một góc nhọn khác là góc �B. Do đó, theo góc cạnh góc đồng dạng, chúng ta có thể kết luận ���ABC đồng dạng với ���HBA.

Vậy nên, ta có: ����=����/2=2����HBAB​=BC/2AB​=2BCAB​ ��2=��×��AB2=BC×HB

b) Tính độ dài cạnh BC và AH

• Độ dài cạnh ��BC: ��=63BC=63​ (đã tính ở trên)
• Độ dài đoạn ��AH: ��AH chính là đoạn cao từ �A xuống ��BC, và trong tam giác vuông ���ABC, ��AH là cạnh huyền. Do đó, ��=��=12 cmAH=AC=12cm.

c) Tính độ dài các đoạn thẳng BD và CD

Tia phân giác của góc �A chia ��BC thành hai đoạn thẳng ��BD và ��CD sao cho: ����=����=912=34CDBD​=ACAB​=129​=43​

��BD và ��CD cũng chính là độ dài của các phân đoạn ��BC theo tỉ lệ 3:43:4.

Vậy: ��=33+4×��=37×63BD=3+43​×BC=73​×63​ ��=43+4×��=47×63CD=3+44​×BC=74​×63​

Vậy là chúng ta đã giải xong bài toán!

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHBA~ΔABC

=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)(1)

=>\(BA^2=BH\cdot BC\)

b: Xét ΔBHA có BM là phân giác

nên \(\dfrac{BH}{BA}=\dfrac{MH}{MA}\left(2\right)\)

Xét ΔBAC có BN là phân giác

nên \(\dfrac{NA}{NC}=\dfrac{BA}{BC}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{MH}{MA}=\dfrac{NA}{NC}\)

=>\(MH\cdot NC=NA\cdot MA\)

\(a.n_{NaOH}=\dfrac{20.20\%}{100\%.40}=0,1mol\\ 2NaOH+CuSO_4\rightarrow Cu\left(OH\right)_2+Na_2SO_4\\ n_{CuSO_4}=n_{Cu\left(OH\right)_2}=n_{Na_2SO_4}=\dfrac{1}{2}n_{NaOH}=0,05mol\\ m_{ddCuSO_4}=\dfrac{0,05.160}{10\%}\cdot100\%=80g\\ b.m_{Cu\left(OH\right)_2}=0,05.98=4,9g\\ c.C_{\%Na_2SO_4}=\dfrac{0,05.142}{20+80-4,9}\cdot100\%=7,46\%\)

Nửa chu vi mảnh vườn là 46:2=23(m)

Gọi chiều rộng mảnh vườn là x(m)

(ĐK: x>0)

Chiều dài mảnh vườn là 23-x(m)

Chiều rộng sau khi tăng thêm 3m là x+3(m)

Chiều dài sau khi tăng thêm 2m là 23-x+2=25-x(m)

Diện tích tăng thêm 67m² nên ta có:
(x+3)(25-x)-x(23-x)=67

=>\(25x-x^2+75-3x-23x+x^2=67\)

=>-x+75=67

=>x=75-67=8(nhận)

vậy: Chiều rộng là 8m

Chiều dài là 23-8=15m

a) Hàm số trên có:

a = -3

b = -2

Đồ thị của hàm số cắt trục tung tại điểm (0; b) nên có tung độ là -2

b) Bảng giá trị:

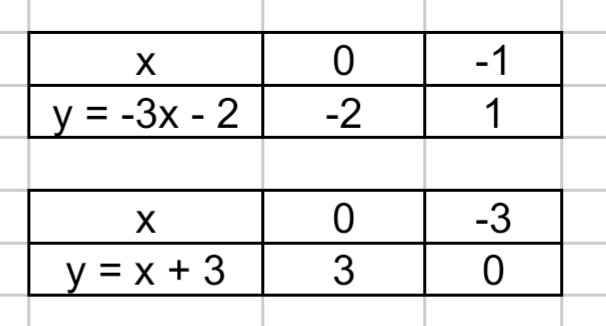
Đồ thị:

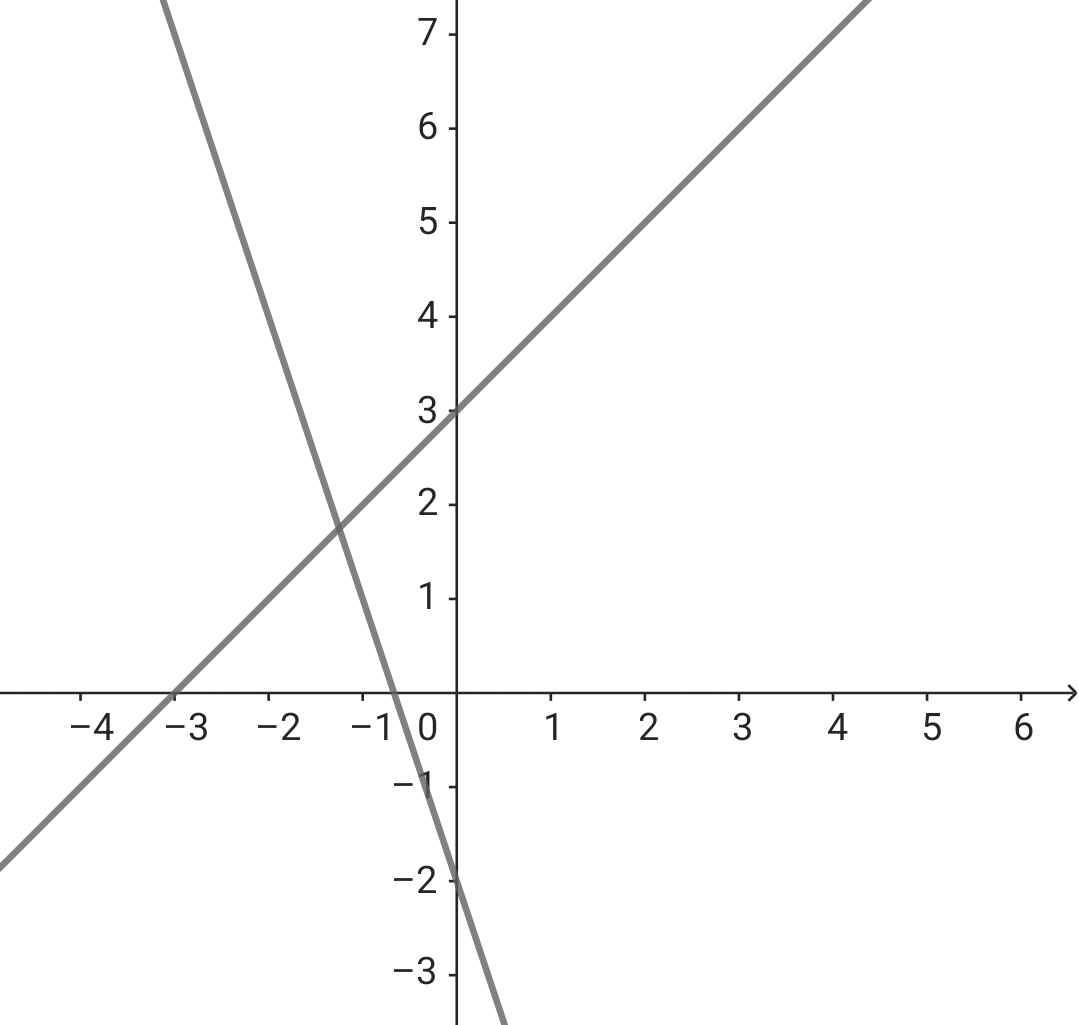
d) Phương trình hoành độ giao điểm của (d) và (d'):

-3x - 2 = x + 3

-3x - x = 3 + 2

-4x = 5

x = -5/4

y = -5/4 + 3 = 7/4

Vậy tọa độ giao điểm của (d) và (d') là (-5/4; 7/4)

Ta có x² - y²= (x+y)(x-y) = 21(x-y) = 189

=> x-y= 189/21 = 9. 

Giá trị x và y tmdk x-y=9 và x+y=21 là x=15, y=6