Có bao nhiêu số khác nhau có 9 chữ số? mà chữ số hàng trăm triệu gấp 3 lần số hàng trăm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không có hình vẽ giả sử mảnh vườn là hình chữ nhật
Nửa chu vi mảnh vườn mới là :
\(88:2=44\left(m\right)\)
Nửa chu vi mảnh vườn ban đầu là :
\(44-\left(2+2\right)=40\left(m\right)\)
Chiều rộng mảnh vườn lúc đầu :
\(40:\left(1+2\right)=\dfrac{40}{3}\left(m\right)\)
Chiều dài mảnh vườn lúc đầu :
\(\dfrac{40}{3}x2=\dfrac{80}{3}\left(m\right)\)
Diện tích mảnh vườn ban đầu :
\(\dfrac{40}{3}x\dfrac{80}{3}=\dfrac{3200}{9}\left(m^2\right)\)

\(\dfrac{2x}{x-1}+\dfrac{3\left(x+1\right)}{x}=5\left(\text{đ}k\text{x}\text{đ}:x\ne1\right)\\ \Leftrightarrow\dfrac{2x^2}{x\left(x-1\right)}+\dfrac{3\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}=\dfrac{5x\left(x-1\right)}{x\left(x-1\right)}\\ \Rightarrow2x^2+\left(3x+3\right)\left(x-1\right)=5x^2-5x\\ \Leftrightarrow2x^2+3x^2-3x+3x-3=5x^2-5x\\ \Leftrightarrow5x^2-3-5x^2+5x=0\\ \Leftrightarrow5x-3=0\\ \Leftrightarrow5x=3\\ \Leftrightarrow x=\dfrac{3}{5}\)
\(b,\left|1-2x\right|=2x-1\) `(1)`
Nếu `1-2x ≥0<=> 2x≥1<=>x≥`\(\dfrac{1}{2}\) thì biểu thức `(1)` trở thành
`1-2x=2x-1`
`<=> 1+1=2x+2x`
`<=> 2=4x`
`<=> -4x=-2`
`<=>x=` \(\dfrac{-2}{-4}=\dfrac{1}{2}\) ( thoả mãn đk )
Nếu `1-2x <0<=> 2x<1<=>x<`\(\dfrac{1}{2}\) thì biểu thức `(1)` trở thành
`-(1-2x)=2x-1`
`<=>-1+2x=2x-1`
`<=> 2x-2x=-1+1`
`<=>0=0` ( luôn đúng )
`c,`
\(\dfrac{2\left(x+1\right)}{3}-2\ge\dfrac{x-2}{2}\\ \Leftrightarrow\dfrac{4\left(x+1\right)}{6}-\dfrac{2}{6}\ge\dfrac{3\left(x-2\right)}{6}\\ \Leftrightarrow4x+4-2\ge3x-6\\ \Leftrightarrow4x+2\ge3x-6\\ \Leftrightarrow4x-3x\ge-6-2\\ \Leftrightarrow x\ge-8\)
a)\(\dfrac{2x}{x-1}+\dfrac{3\left(x+1\right)}{x}=5\)
\(\dfrac{x\cdot2x}{x\left(x-1\right)}+\dfrac{3\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}=5\)
\(\dfrac{2x^2}{x^2-x}+\dfrac{3\left(x^2-1^2\right)}{x^2-x}=5\)
\(\dfrac{2x^2}{x^2-x}+\dfrac{3x^2-3}{x^2-x}=5\)
\(\dfrac{2x^2+3x^2-3}{x^2-x}=\dfrac{5x^2-3}{x^2-x}=5\)
\(\Rightarrow5x^2-3=5\left(x^2-x\right)=5x^2-5x\)
\(\Rightarrow3=5x\)
\(x=\dfrac{3}{5}\)
b) \(\left|1-2x\right|=2x-1\)
TH1: \(1>2x\)
\(\Rightarrow\left[{}\begin{matrix}1-2x>0\\2x-1< 0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left|1-2x\right|>0\\2x-1< 0\end{matrix}\right.\) => Vô lí
TH2: \(1\le2x\)
\(\Rightarrow\left[{}\begin{matrix}1-2x\le0\Rightarrow\left|1-2x\right|\ge0\\2x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left|1-2x\right|=2x-1\ge0\)
\(\Leftrightarrow2x-1\ge0\Rightarrow2x-1+1=2x\ge0+1=1\)
\(\Leftrightarrow\dfrac{2x}{2}=x\ge\dfrac{1}{2}\)

Lời giải:
$\widehat{M_1}-\widehat{M_2}=\widehat{N_1}-\widehat{N_2}(1)$
$\widehat{M_1}+\widehat{M_2}=\widehat{N_1}+\widehat{N_2}(2)$ (cùng bằng $180^0$)
Lấy $(1)+(2)$ và thu gọn thì $\widehat{M_1}=\widehat{N_1}$
Mà 2 góc này ở vị trí so le trong nên $m\parallel n$

Đề bài bạn viết khó hiểu quá. Bạn nên viết lại rõ ràng, mạch lạc, có ngắt nghỉ và xuống dòng hợp lý.

\(\Rightarrow\left(x+x+x+x\right)+\left(3,2+1,8+1,7+2,3\right)=25,2\)
\(\Rightarrow4x+9=25,2\)
\(\Rightarrow4x=16,2\Rightarrow x=4,05\)

Lời giải:
Các số tự nhiên chia 5 dư 3 có dạng $5k+3$ với $k\in\mathbb{N}$
$5k+3< 240$
$\Rightarrow k< 47,4$
$k$ là số tự nhiên nên $k\in \left\{0; 1; 2;...; 47\right\}$
Có 48 giá trị k thỏa mãn nên tương ứng có 48 số tự nhiên thỏa mãn đề.

Xét các số có 4 chữ số thỏa mãn yêu cầu bài toán thì số thứ nhất, số thứ 2, số thứ 3 đều có 6 cách chọn. Riêng số cuối cùng thì chỉ có 1 cách chọn (là chữ số 5 vì số có 4 chữ số phải chia hết cho 5) nên ta lập được tất cả \(6.6.6.1=216\) (số)

\(2\left(a^2+b^2\right)=\left(a-b\right)^2\)
\(\Rightarrow2a^2+2b^2=a^2-2ab+b^2\)
\(\Rightarrow a^2+b^2+2ab=0\)
\(\Rightarrow\left(a+b\right)^2=0\)
\(\Rightarrow a+b=0\Rightarrow a=-b\Rightarrow dpcm\)

\(9734-2.x=168\Rightarrow2x=9734-168\Rightarrow2x=9566\Rightarrow x=4783\)
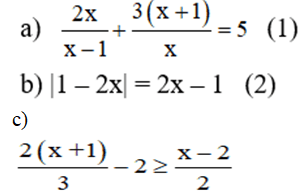

1 tỉ 300 trăm triệu lẻ 1 trăm,mỗi lần qua 1 tỉ sẽ có 3 chữ số,
3 x 9 = 27