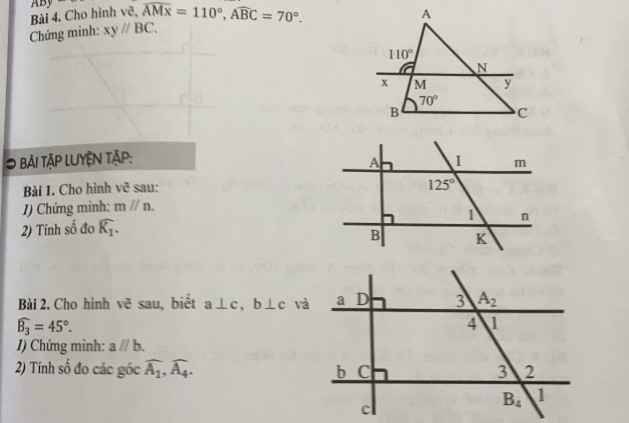
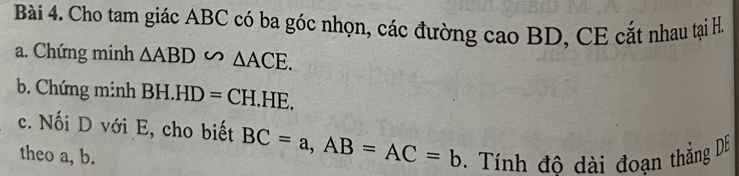Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(M=ab.\left(a^2-b^2\right).\left(a^2+b^2\right)\)
cần CM biểu thức trên chia hết cho đổng thời cả 2;3;5
đầu tiên là CM chia hết cho 2 nhé
nếu a,b khác tính chẵn lẻ thì dễ rồi nhé
nếu chúng cùng tính chẵn lẻ thì \(a^2-b^2\) chia hết cho 2
vì vậy nên M chia hết cho 2
+) CM chia hết cho 3
nếu mà a hoặc b hay cả 2 cái đều chia hết cho 3 thì dễ nhé vì M có tích ab
nếu mà cả a và b ko chia hết cho 3
\(\Rightarrow\left\{{}\begin{matrix}a^2\equiv1\left(mod3\right)\\b^2\equiv1\left(mod3\right)\end{matrix}\right.\)
\(\Rightarrow a^2-b^2⋮3\)
\(\Rightarrow M⋮3\forall a,b\in Z\)
+)CM chia hết cho 5
nếu a.b chia hết cho 5 thì rất dễ rồi nhé
nếu a,b ko chia hết cho 5 thì:
\(a^2\equiv\pm1\left(mod5\right)\)
\(b^2\equiv\pm1\left(mod5\right)\)
nếu mà \(a^2\equiv b^2\left(mod5\right)\) thì \(a^2-b^2⋮5\)
nế mà chúng khác số dư tức là 1 cái dư 1,một cái dư -1 thì \(a^2+b^2⋮5\) nhé
\(\Rightarrow M⋮5\forall a,b\in Z\)
mà \(\left(2;3;5\right)=1\)
\(\Rightarrow M⋮2.3.5=30\)(đpcm)

\(\left(x+3\right).\left(x^2-3x+5\right)=x^2+3x\)
\(\Leftrightarrow\left(x+3\right).\left(x^2-3x+5\right)-x.\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right).\left(x^2-4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2-4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x^2-4x+5=0\end{matrix}\right.\)
+)\(x^2-4x+5=\left(x-2\right)^2+1>0\) nên loại
phương trình 2 dễ nên bạn làm tương tự nhé