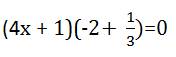
a: Xét ΔADB và ΔADC có

AB=AC
góc BAD=góc CAD

AD chung

=>ΔADB=ΔADC

b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có

AD chung

góc EAD=góc FAD

=>ΔAED=ΔAFD
=>AE=AF và DE=DF

c: Xét ΔABC có AE/AB=AF/AC

nên EF//BC

C nha

sao lại c vậy cou, gth giúp mik

\(\dfrac{x}{2}-\left(\dfrac{3x}{5}-\dfrac{13}{5}\right)=\dfrac{7}{5}+\dfrac{7}{10}x\\ \Rightarrow\dfrac{x}{2}-\dfrac{3x}{5}+\dfrac{13}{5}=\dfrac{7}{5}+\dfrac{7x}{10}\\ \Rightarrow\dfrac{5x}{10}-\dfrac{6x}{10}+\dfrac{26}{10}=\dfrac{14}{10}+\dfrac{7x}{10}\\ \Rightarrow\dfrac{5x}{10}-\dfrac{6x}{10}-\dfrac{7x}{10}=\dfrac{14}{10}-\dfrac{26}{10}\\ \Rightarrow\dfrac{-8x}{10}=-\dfrac{12}{10}\\ \Rightarrow\dfrac{-4x}{5}=-\dfrac{6}{5}\\ \Rightarrow-20x=-30\\ \Rightarrow x=\dfrac{3}{2}\)

Gọi số tuổi cách đây 2 năm và tuổi em sau 4 năm lần lượt là \(a,b\)

\(\Rightarrow\dfrac{a-2}{15}=\dfrac{b+4}{16}\) và \(a+b=5\)

Áp dụng tính chất dãy tỉ sổ bằng nhau ta có:

\(\dfrac{a-2}{15}=\dfrac{b+4}{16}=\dfrac{a-2-b-4}{15-16}=\dfrac{5-6}{-1}=\dfrac{-1}{-1}=1\)

\(\left\{{}\begin{matrix}a-2=15\Rightarrow a=15+2\Rightarrow a=17\\\\\\a+4=16\Rightarrow a=16-4\Rightarrow a=12\end{matrix}\right.\)

Vậy tuổi anh và em lần lượt là: \(17;12\) tuổi.

Gọi tuổi em hiện nay là: \(x\) (tuổi) \(x\) \(\in\) N*

Tuổi anh hiện nay là: \(x\) + 5 (tuổi)

Tuổi anh cách đây hai năm là: \(x\) + 5 - 2 = \(x\) + 3 (tuổi)

tuổi em sau bốn năm nữa là: \(x\) + 4 (tuổi)

Theo bài ra ta có: \(\dfrac{x+3}{15}\) = \(\dfrac{x+4}{16}\) ⇒ 16.(\(x\) + 3) = 15.(\(x\) + 4)

                        ⇒16 \(x\) + 48 = 15\(x\) + 60 ⇒ \(x\) = 60 - 48 = 12

Tuổi em anh hiện nay là: 12 + 5 = 17 (tuổi)

Kết luận:  Em hiện nay 12 tuổi; anh hiện nay 17 tuổi.

\(D=\dfrac{15}{3\left|2x+1\right|+5}\)

Ta có:

\(\left\{{}\begin{matrix}15>0\\3\left|2x+1\right|\ge5\forall x\end{matrix}\right.\)Nên:

\(\Rightarrow D=\dfrac{15}{3\left|2x-1\right|+5}\le3\left(=\dfrac{15}{5}\right)\forall x\) 

Dấu "=" xảy ra:

\(\dfrac{15}{3\left|2x+1\right|+5}=3\)

\(\Rightarrow3\left|2x+1\right|+5=5\)

\(\Rightarrow3\left|2x+1\right|=0\)

\(\Rightarrow\left|2x+1\right|=0\)

\(\Rightarrow2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=-\dfrac{1}{2}\)

Vậy: \(D_{max}=3\) khi \(x=-\dfrac{1}{2}\)

D = \(\dfrac{15}{3.\left|2x-1\right|+5}\)  vì |2\(x\) - 1| ≥ 0 ∀ \(x\) ⇒3.|2\(x-1\)| + 5 ≥ 5 ∀ \(x\)

⇒D = \(\dfrac{15}{3.\left|2x-1\right|+5}\) ≤ \(\dfrac{15}{5}\) = 3 dấu bằng xảy ra khi 2\(x\) - 1 =0 ⇒ \(x=\dfrac{1}{2}\)

Kết luận D_min = 3 ⇔ \(x\) = \(\dfrac{1}{2}\)

a)

Vì tam giác ABC cân tại A (gt)

=> AB = AC (TC tam giác cân)

Xét tam giác ABM và tam giác ACM có:

AB = AC (CMT)

AM chung

BM = CM (AM là đường trung tuyến)

=> tam giác ABM = tam giác ACM (c - c - c)

a. \(\dfrac{1}{2.4}\) + \(\dfrac{1}{4.6}\) + \(\dfrac{1}{6.8}\) + ...... + \(\dfrac{1}{20.22}\)

= 1/2 ( 1/2 - 1/4 + 1/4 - 1/6 + 1/6 - 1/8 + ..... + 1/20 - 1/22)

=1/2 ( 1/2 - 1/22)

= 1/2 . 5/11

= 5/22

b. 1+ 2/3 + 2/6 + 2/10 +...+ 2/45

=>1/2.(1+2/3+2/6+....+2/45)=1/2+2/6+2/12+...+2/90

=1/2+2/2.3+2/3.4+...+2/9.10
=2.(1/4+3-2/2.3+4-3/3.4+...+10-9/9.10)

=2. ( 1/4+1/2-1/3+1/3-1/4+.....+1/9-1/10)
= 2.( 1/4-1/10)=2.3/20=3/10

=> vì 1/2.*=3/10

=> *=3/10:1/2=3/5

tick mình nhé

B = 1 + \(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) +\(\dfrac{2}{10}\) + \(\dfrac{2}{15}\)+...+ \(\dfrac{2}{45}\)

B = 1 + 2.(\(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + \(\dfrac{1}{15}\)+...+ \(\dfrac{1}{45}\))

B = 1 + \(\dfrac{4}{2}\).(\(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) +\(\dfrac{1}{10}\) + \(\dfrac{1}{15}\) + ...+ \(\dfrac{1}{45}\))

B = 1 + 4.( \(\dfrac{1}{6}\) +\(\dfrac{1}{12}\)+ \(\dfrac{1}{20}\)+ \(\dfrac{1}{30}\)+...+ \(\dfrac{1}{90}\))

B = 1 + 4.(\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\)+ \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\)+...+\(\dfrac{1}{9.10}\))

B = 1 + 4 .( \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)+...+ \(\dfrac{1}{9}\) - \(\dfrac{1}{10}\))

B = 1 + 4.( \(\dfrac{1}{2}\) - \(\dfrac{1}{10}\))

B = 1 + 4. \(\dfrac{2}{5}\)

B = \(\dfrac{13}{5}\)

\(\left(4x+1\right)\left(-2+\dfrac{1}{3}\right)=0\\ \Rightarrow\left(4x+1\right)\left(-\dfrac{6}{3}+\dfrac{1}{3}\right)=0\\ \Rightarrow\left(4x+1\right)\left(-\dfrac{5}{3}\right)=0\\ \Rightarrow4x+1=0:\left(-\dfrac{5}{3}\right)\\ \Rightarrow4x+1=0\\ \Rightarrow4x=0-1\\ \Rightarrow4x=-1\\ \Rightarrow x=-\dfrac{1}{3}\)

\(\dfrac{1}{7}-\dfrac{3}{5}x\text{=}\dfrac{3}{5}\)

\(\dfrac{3}{5}x\text{=}\dfrac{1}{7}-\dfrac{3}{5}\)

\(\dfrac{3}{5}x\text{=}\dfrac{-16}{35}\)

\(x\text{=}\dfrac{-16}{35}:\dfrac{3}{5}\)

\(x\text{=}\dfrac{-16}{21}\)