0.275 + \(\left(\dfrac{-8}{17}\right)\) + \(\dfrac{29}{40}\) + \(\left(\dfrac{-9}{17}\right)\) - \(1\dfrac{1}{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


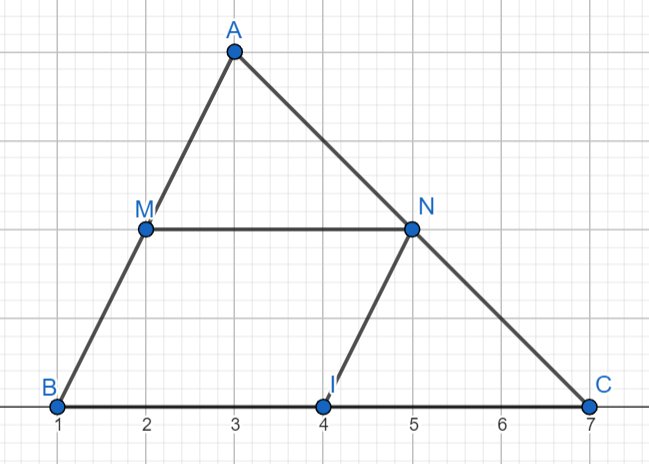
Đề sai rồi bạn, theo đề thì \(MN\) là đường trung bình của \(\triangle ABC\)
nên \(MN//BC\Rightarrow\widehat {AMN}=\widehat{NIC}\) (hai góc đồng vị)
Vì vậy nếu \(\widehat{AMN}=\widehat{INC}\) thì \(\widehat{NIC}=\widehat{INC}\)
\(\Rightarrow\triangle INC\) cân tại C
Từ đây xảy ra trường hợp đặc biệt \(\rightarrow\) đề sai

Tuổi của hai chị em mỗi năm tăng lên 1 tuổi nên hiệu tuổi hai chị em vẫn là 5
Tuổi của em hiện nay là :
\(\left(21-5\right):2=8\) ( tuổi )
Tuổi của chị hiện nay là :
\(21-8=13\) ( tuổi )
Đáp số : em : 8 tuổi ; chị : 13 tuổi
Tuổi của em hiện nay là (21-5):2=8(tuổi)
Tuổi của chị hiện nay là 21-8=13(tuổi)

\(230-x\times3=50\)
\(x\times3=230-50\)
\(x\times3=180\)
\(x=180:3\)
\(x=60\)
Vậy \(x=60\)
230 - X x 3 = 50
X x 3 = 230 - 50
X x 3 = 180
X = 180 : 3
X = 60

\(\dfrac{-3}{100}=\dfrac{-3\cdot3}{100\cdot3}=\dfrac{-9}{100};\dfrac{2}{-3}=\dfrac{-2}{3}=\dfrac{-2\cdot100}{3\cdot100}=\dfrac{-200}{300}\)
mà -9>-200
nên \(\dfrac{-3}{100}>\dfrac{2}{-3}\)
Ta có :
+) \(\dfrac{2}{-3}=\dfrac{-2}{3}=\dfrac{-6}{9}\)
+) \(\dfrac{-3}{100}=\dfrac{-6}{200}\)
Vì \(9< 200\Rightarrow\dfrac{6}{9}>\dfrac{6}{200}\Rightarrow\dfrac{-6}{9}< \dfrac{-6}{200}\)
\(\Rightarrow\dfrac{2}{-3}< \dfrac{-3}{100}\)

\(A=sin^210^0+sin^220^0+sin^245^0+sin^270^0+sin^280^0\)
\(=\left(sin^210^0+sin^280^0\right)+\left(sin^220^0+sin^270^0\right)+sin^245^0\)
\(=\left(sin^210^0+cos^210^0\right)+\left(sin^220^0+cos^220^0\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)
\(B=tan20^0\cdot tan35^0\cdot tan45^0\cdot tan55^0\cdot tan20^0\)
\(=tan^220^0\cdot tan35^0\cdot cot35^0\cdot1=tan^220^0\)
\(C=3\cdot\left(sin^4\alpha+cos^4\alpha\right)-2\left(sin^6\alpha+cos^6\alpha\right)\)
\(=3\left[\left(sin^2\alpha+cos^2\alpha\right)^2-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[\left(sin^2\alpha+cos^2\alpha\right)^3-3\cdot sin^2\alpha\cdot cos^2\alpha\cdot\left(sin^2\alpha+cos^2\alpha\right)\right]\)
\(=3\left[1-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[1-3\cdot sin^2\alpha\cdot cos^2\alpha\right]\)
\(=3-6\cdot sin^2\alpha\cdot cos^2\alpha-2+6\cdot sin^2\alpha\cdot cos^2\alpha\)
=1
\(D=\sqrt{sin^2\alpha}+4\cdot cos^2\alpha+\sqrt{cos^2\alpha}+4\cdot sin^2\alpha\)
\(=\left|sin\alpha\right|+\left|cos\alpha\right|+4\cdot\left(cos^2\alpha+sin^2\alpha\right)=\left|sin\alpha\right|+\left|cos\alpha\right|+4\)

a: \(cos\left(x-15^0\right)=\dfrac{\sqrt{2}}{2}\)
=>\(\left[{}\begin{matrix}x-15^0=45^0+k\cdot360^0\\x-15^0=-45^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=60^0+k\cdot360^0\\x=-30^0+k\cdot360^0\end{matrix}\right.\)
b: \(cos\left(2x+\dfrac{\Omega}{3}\right)+cos\left(x-\dfrac{\Omega}{3}\right)=0\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=-cos\left(x-\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(\Omega-x+\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(-x+\dfrac{4\Omega}{3}\right)\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{3}=-x+\dfrac{4\Omega}{3}+k2\Omega\\2x+\dfrac{\Omega}{3}=x-\dfrac{4}{3}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\Omega+k2\Omega\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+\dfrac{k2\Omega}{3}\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
c: \(sin\left(3x+1\right)=sin\left(x-2\right)\)
=>\(\left[{}\begin{matrix}3x+1=x-2+k2\Omega\\3x+1=\Omega-x+2+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-3+k2\Omega\\4x=1+\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}+k\Omega\\x=\dfrac{1}{4}+\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\end{matrix}\right.\)

Bài 3:
1/2 của 16 là \(16\times\dfrac{1}{2}=\dfrac{16}{2}=8\)
1/5 của 20 là \(20\times\dfrac{1}{5}=\dfrac{20}{5}=4\)
Bài 2: Hình tròn này có 4 phần
Bài 1:
55+7=62
45+7=52
56+9=65
Bài 4:
Nếu năm 2024 bạn đang học lớp 4 thì có nghĩa là bạn 9 tuổi
=>Năm sinh của bạn là 2024-9=2015
=>Năm 2009 thì vào thời điểm đó, bạn chưa ra đời

\(24:6+36:6\)
\(=\left(24+36\right):6\)
\(=60:6\)
\(=10\)

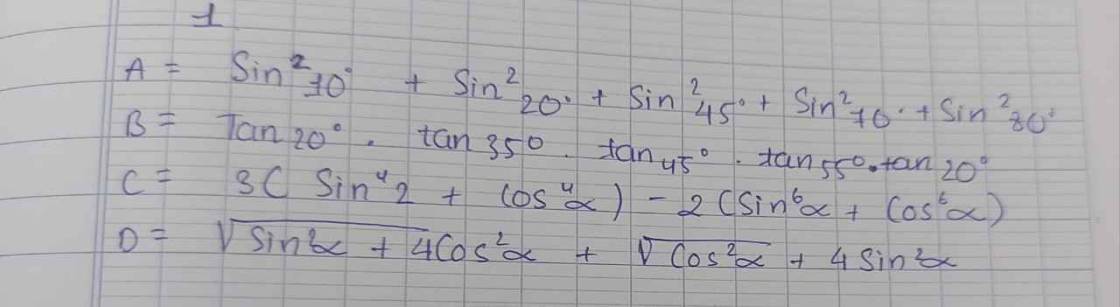
\(0,275+\left(\dfrac{-8}{17}\right)+\dfrac{29}{40}+\left(\dfrac{-9}{17}\right)-1\dfrac{1}{3}\)
\(=\dfrac{11}{40}-\dfrac{8}{17}+\dfrac{29}{40}-\dfrac{9}{17}-\dfrac{4}{3}\)
\(=\left(\dfrac{11}{40}+\dfrac{29}{40}\right)-\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{4}{3}\)
\(=1-1-\dfrac{4}{3}\)
\(=-\dfrac{4}{3}\)
\(0,275+\left(-\dfrac{8}{17}\right)+\dfrac{29}{40}+\left(-\dfrac{9}{17}\right)-1\dfrac{1}{3}\)
\(=\left(\dfrac{11}{40}+\dfrac{29}{40}\right)+\left(-\dfrac{8}{17}-\dfrac{9}{17}\right)-\dfrac{4}{3}\)
\(=1-1-\dfrac{4}{3}=-\dfrac{4}{3}\)