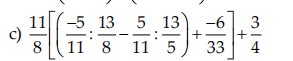
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
\(a.\dfrac{3x+2}{x-3}=\dfrac{3x-9+11}{x-3}=\dfrac{3\left(x-3\right)+11}{x-3}=3+\dfrac{11}{x-3}\)
Để bt nguyên thì 11 ⋮ x - 3
=> x - 3 ∈ Ư(11) = {1; -1; 11; -11}
=> x ∈ {4; 2; 14; -8}
\(b.\dfrac{x-2}{3x-2}\) nguyên \(\Rightarrow\dfrac{3\left(x-2\right)}{3x-2}=\dfrac{3x-6}{3x-2}=\dfrac{3x-2-4}{3x-2}=1-\dfrac{4}{3x-2}\)
Để bt nguyên thì: 4 ⋮ 3x - 2
=> 3x - 2 ∈ Ư(4) = {1; -1; 2; -2; 4; -4}
=> 3x ∈ {3; 1; 4; 0; 5; -2}
=> x ∈ {1; `1/3`; `4/3`; 0;`5/3`;`-2/3`}
Mà: x nguyên => x ∈ {1;0}
Bài 4:
\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\)
=>\(3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\)
=>\(3A+A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3+3^{100}-3^{99}+...+3^2-3+1\)
=>\(4A=3^{101}+1\)
=>\(A=\dfrac{3^{101}+1}{4}\)

(35 x 2 - 35:5 x 10) x (1 + 3 + 5 + ... + 19)
= [35 x 2 - 35 x (10 : 5) ] x (1 + 3 + 5 + ... + 19)
= (35 x 2 - 35 x 2) x (1 + 3 + 5 +... + 19)
= (70 - 70) x (1 + 3 + 5 + .... + 19)
= 0 x (1 + 3 + 5 + ... + 19)
= 0
(35 x 2 - 35: 5 x 10) x (1 + 3 + 5 + ... + 17 + 19)
= (70 - 7 x 10) x (1 + 3 + 5 + ... + 17 + 19)
= (70 - 70) x (1 + 3 + 5 + ... + 17 + 19)
= 0 x (1 + 3 + 5 + ... +17 + 19)
= 0

a)
\(\dfrac{24\cdot47-23}{24+47\cdot23}\cdot\dfrac{3+\dfrac{3}{7}-\dfrac{3}{11}+\dfrac{3}{101}-\dfrac{3}{13}}{\dfrac{6}{101}-\dfrac{6}{13}+\dfrac{6}{7}-\dfrac{6}{11}+6}\\ =\dfrac{\left(23+1\right)\cdot47-23}{24+47\cdot23}\cdot\dfrac{3\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}{6\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}\\ =\dfrac{23\cdot47+47-23}{23\cdot47+24}\cdot\dfrac{3}{6}\\ =\dfrac{23\cdot47+24}{23\cdot47+24}\cdot\dfrac{1}{2}\\ =1\cdot\dfrac{1}{2}=\dfrac{1}{2}\)
b)
\(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{19\cdot21}\\ =\dfrac{1}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{3}{19\cdot21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\dfrac{20}{21}\\ =\dfrac{10}{21}\)

\(B=\dfrac{2024\cdot2025-2000}{2023\cdot2024+2048}\\ =\dfrac{\left(2023+2\right)\cdot2024-2000}{2023\cdot2024+2048}\\ =\dfrac{2023\cdot2024+2\cdot2048-2000}{2023\cdot2024+2048}\\ =\dfrac{2023\cdot2024+4048-2000}{2023\cdot2024+2048}\\ =\dfrac{2023\cdot2024+2048}{2023\cdot2024+2048}\\ =1\)
Mà: \(A=1+\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{1}{210}=1+\left(\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{1}{210}\right)\)
\(\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{1}{210}>0\Rightarrow A>1\Rightarrow A>B\)

Xét ΔADE vuông tại D có \(cosA=\dfrac{AD}{AE}\)
=>\(\dfrac{AD}{4}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(AD=4\cdot\dfrac{\sqrt{3}}{2}=2\sqrt{3}\left(cm\right)\)
D là trung điểm của AB
=>\(AB=2\cdot AD=4\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại C có \(sinA=\dfrac{BC}{AB}\)
=>\(\dfrac{BC}{4\sqrt{3}}=sin30=\dfrac{1}{2}\)
=>\(BC=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}\left(cm\right)\)


Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
=>D nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AD là đường trung trực của BE
=>AD\(\perp\)BE


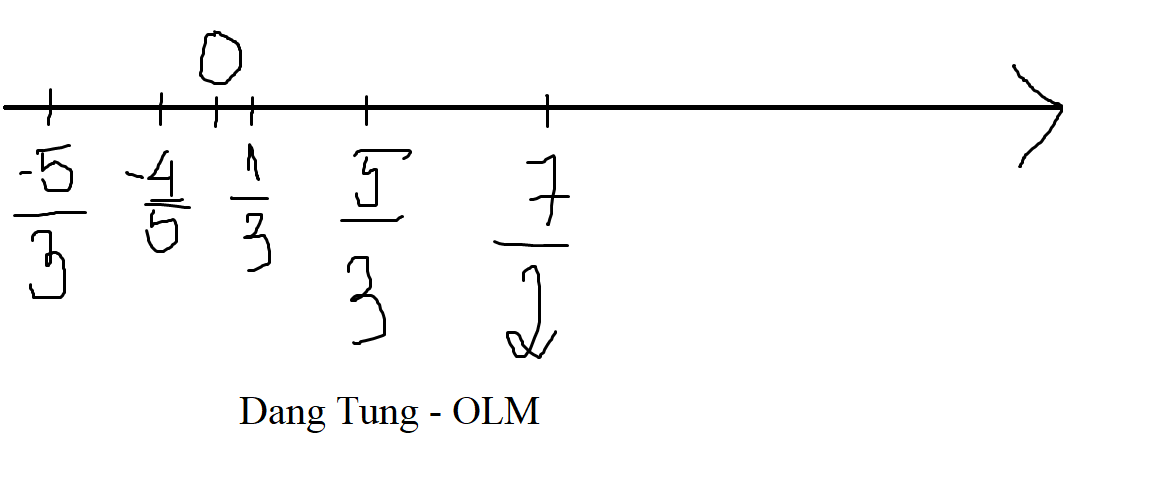
\(\dfrac{11}{8}\left[\left(\dfrac{-5}{11}:\dfrac{13}{8}-\dfrac{5}{11}:\dfrac{13}{5}\right)+\dfrac{-6}{33}\right]+\dfrac{3}{4}\\ =\dfrac{11}{8}\left[\left(\dfrac{-5}{11}\cdot\dfrac{8}{13}+\dfrac{-5}{11}\cdot\dfrac{5}{13}\right)+\dfrac{-2}{11}\right]+\dfrac{3}{4}\\ =\dfrac{11}{8}\left[\dfrac{-5}{11}\cdot\left(\dfrac{8}{13}+\dfrac{5}{13}\right)+\dfrac{-2}{11}\right]+\dfrac{3}{4}\\ =\dfrac{11}{8}\left(\dfrac{-5}{11}+\dfrac{-2}{11}\right)+\dfrac{3}{4}\\ =\dfrac{11}{8}\cdot\dfrac{-7}{11}+\dfrac{3}{4}\\ =\dfrac{-7}{8}+\dfrac{6}{8}\\ =\dfrac{-1}{8}\)