Tính giới hạn $\lim\limits_{x\rightarrow 1^+} \dfrac{4x-3}{x-1}$ bằng định nghĩa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt f(x)=cosx.
Chọn hai dãy số {xn} và {yn} với :
* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :
f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .
* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :
f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.
Vậy limx→∞cosx không tồn tại.
Hai câu kia của mình bị lỗi ,không biết câu này có bị không
Đặt f(x)=cosx.
Chọn hai dãy số {xn} và {yn} với :
* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :
f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .
* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :
f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.
Vậy limx→∞cosx không tồn tại.
Hai câu kia mình bị lỗi nha.

\(\hept{\begin{cases}lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^+}\frac{x-3}{x-3}=1\\lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^-}\frac{-x+3}{x-3}=-1\end{cases}\Rightarrow lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}\ne lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}}\)
=> đpcm

Ta có limx→0−f(x)=limx→0−(mx+m+14)=m+14limx→0−f(x)=limx→0−(mx+m+14)=m+14.
limx→0+f(x)=limx→0+√x+4−2x=limx→0+x+4−4x(√x+4+2)=limx→0+1√x+4+2=14limx→0+f(x)=limx→0+x+4−2x=limx→0+x+4−4x(x+4+2)=limx→0+1x+4+2=14.
Để hàm số có giới hạn tạix=0x=0 thì limx→0−f(x)=limx→0+f(x)⇔m+14=14⇔m=0limx→0−f(x)=limx→0+f(x)⇔m+14=14⇔m=0.

gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)

Hai mặt phẳng (AB′D′)(AB′D′) và (A′C′D)(A′C′D) có giao tuyến là EFEF như hình vẽ.
Hai tam giácΔA′C′D=ΔD′AB′ΔA′C′D=ΔD′AB′và EFEF là đường trung bình của hai tam giác nên từ A′A′ và D′D′ ta kẻ 2 đoạn vuông góc lên giao tuyến EFEF sẽ là chung một điểm HH như hình vẽ.
Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng A′HA′H và D′HD′H.
Tam giác DEFDEF lần lượt cóD′E=D′B′2=√132D′E=D′B′2=132,D′F=D′A2=52D′F=D′A2=52,EF=B′A2=√5EF=B′A2=5.
Theo hê rông ta có:SDEF=√614SDEF=614. Suy raD′H=2SDEFEF=√30510D′H=2SDEFEF=30510.
Tam giác D′A′HD′A′H có:cosˆA′HD′=HA′2+HD′2−A′D′22HA′.HD′=−2961cosA′HD′^=HA′2+HD′2−A′D′22HA′.HD′=−2961.
Do đóˆA′HD′≈118,4∘A′HD′^≈118,4∘hay(ˆA′H,D′H)≈180∘−118,4∘=61,6∘(A′H,D′H^)≈180∘−118,4∘=61,6∘.
là hình chiếu vuông góc của trên .
là hình chiếu vuông góc của trên mặt phẳng .
Do đó với là góc cần tìm.
Ta có .
.
Dùng công thức Hê rông ta có .
Vậy .

Hai mặt phẳng (AB′D′)(AB′D′) và (A′C′D)(A′C′D) có giao tuyến là EFEF như hình vẽ.
Hai tam giác ΔA′C′D=ΔD′AB′ΔA′C′D=ΔD′AB′ và EFEF là đường trung bình của hai tam giác nên từ A′A′ và D′D′ ta kẻ 2 đoạn vuông góc lên giao tuyến EFEF sẽ là chung một điểm HH như hình vẽ.
Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng A′HA′H và D′HD′H.
Tam giác DEFDEF lần lượt có D′E=D′B′2=√132D′E=D′B′2=132, D′F=D′A2=52D′F=D′A2=52, EF=B′A2=√5EF=B′A2=5.
Theo hê rông ta có: SDEF=√614SDEF=614. Suy ra D′H=2SDEFEF=√30510D′H=2SDEFEF=30510.
Tam giác D′A′HD′A′H có: cosˆA′HD′=HA′2+HD′2−A′D′22HA′.HD′=−2961cosA′HD′^=HA′2+HD′2−A′D′22HA′.HD′=−2961.
Do đó ˆA′HD′≈118,4∘A′HD′^≈118,4∘ hay (ˆA′H,D′H)≈180∘−118,4∘=61,6∘(A′H,D′H^)≈180∘−118,4∘=61,6∘.
Gọi và lần lượt là trung điểm của và .
Theo tính chất đường trung bình trong tam giác ta có và .
Suy ra .
Ta có và ;\\
.
Vậy .2/5

Ta có {BC⊥ABAB⊥SC⇒AB⊥CE{BC⊥ABAB⊥SC⇒AB⊥CE
Khi đó {CE⊥ABCE⊥SA⇒CE⊥(SAB){CE⊥ABCE⊥SA⇒CE⊥(SAB)
Áp dụng hệ thức lượng trong tam giác vuông ta có: SC2=SE.SB⇒SESB=SC2SB2SC2=SE.SB⇒SESB=SC2SB2, tương tự SDSE=SC2SA2SDSE=SC2SA2
Lại cả CA=AC√2=2a;VS.ABC=13SC.SABC=23a3CA=AC2=2a;VS.ABC=13SC.SABC=23a3
Khi đó VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13
Do đó VS.CDE=13.23a3=2a39VS.CDE=13.23a3=2a39.


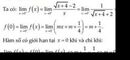

Với mọi dãy (xn):xn>1
\(\forall\)n và \(limx_n=1\)ta có \(lim_{x\rightarrow1^+}\frac{4x-3}{x-1}=lim\frac{4x_n-3}{x_n-1}=+\infty\)