 cần gấp ạ 🫰🏻
cần gấp ạ 🫰🏻
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 tấn=1000kg
Ngày thứ hai bán được: 300x2=600(kg)
Ngày thứ ba bán được: 1000-300-600=100(kg)
giải
1 tấn=1000kg
Ngày thứ hai bán được:
300x2=600(kg)
Ngày thứ ba bán được:
1000-300-600=100(kg)
Đ/s: 100kg
tick cho mình đi mà

\(12,74+38,22+37,26\)
\(=\left(12,74+37,26\right)+38,22\)
=50+38,22
=88,22

Câu 3:
1: \(\sqrt{\dfrac{1}{4}}=\dfrac{\sqrt{1}}{\sqrt{4}}=\dfrac{1}{2}\)
2: \(\sqrt{\dfrac{25}{49}}=\dfrac{\sqrt{25}}{\sqrt{49}}=\dfrac{5}{7}\)
3: \(\sqrt{\dfrac{64}{81}}=\dfrac{\sqrt{64}}{\sqrt{81}}=\dfrac{8}{9}\)
4: \(\sqrt{\dfrac{100}{9}}=\dfrac{\sqrt{100}}{\sqrt{9}}=\dfrac{10}{3}\)
5: \(\sqrt{\dfrac{17+8}{16}}=\sqrt{\dfrac{25}{16}}=\dfrac{\sqrt{25}}{\sqrt{16}}=\dfrac{5}{4}\)
6: \(\sqrt{\dfrac{36}{100-36}}=\sqrt{\dfrac{36}{64}}=\sqrt{\dfrac{9}{16}}=\dfrac{\sqrt{9}}{\sqrt{16}}=\dfrac{3}{4}\)
7: \(\sqrt{1-\dfrac{11}{36}}=\sqrt{\dfrac{36}{36}-\dfrac{11}{36}}=\sqrt{\dfrac{25}{36}}=\dfrac{\sqrt{25}}{\sqrt{36}}=\dfrac{5}{6}\)
8: \(\sqrt{2+\dfrac{1}{4}}=\sqrt{\dfrac{9}{4}}=\dfrac{\sqrt{9}}{\sqrt{4}}=\dfrac{3}{2}\)
Câu 5:
1: ĐKXĐ: x>=0
\(\sqrt{x}+\dfrac{1}{3}=\dfrac{1}{4}\)
=>\(\sqrt{x}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)<0(vô lý)
=>Phương trình vô nghiệm
2: ĐKXĐ: x>=0
\(2-3\sqrt{x}=-7\)
=>\(3\sqrt{x}=2+7=9\)
=>\(\sqrt{x}=3\)
=>\(x=3^2=9\)(nhận)
3: ĐKXĐ: x+1>=0
=>x>=-1
\(\sqrt{x+1}=1\)
=>\(x+1=1^2=1\)
=>x=1-1=0(nhận)
4: ĐKXĐ: x>=0
\(\dfrac{3}{5}\sqrt{x}-\dfrac{2}{3}=\dfrac{4}{5}\)
=>\(\dfrac{3}{5}\sqrt{x}=\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{10}{15}+\dfrac{12}{15}=\dfrac{22}{15}\)
=>\(\sqrt{x}=\dfrac{22}{15}:\dfrac{3}{5}=\dfrac{22}{15}\cdot\dfrac{5}{3}=\dfrac{110}{45}=\dfrac{22}{9}\)
=>\(x=\left(\dfrac{22}{9}\right)^2=\dfrac{264}{81}\)
5: ĐKXĐ: 2x-7>=0
=>x>=7/2
\(\sqrt{2x-7}=5\)
=>\(2x-7=5^2=25\)
=>2x=7+25=32
=>x=32/2=16(nhận)
6: ĐKXĐ: 2-3x>=0
=>3x<=2
=>\(x< =\dfrac{2}{3}\)
\(\sqrt{2-3x}=4\)
=>\(2-3x=4^2=16\)
=>3x=2-16=-14
=>\(x=-\dfrac{14}{3}\left(nhận\right)\)

chiều dài mới của mảnh đất là:
\(15+15\times\dfrac{1}{5}=18\left(m\right)\)
Chiều rộng của mảnh đất ban đầu là:
27:(18-15)=27:3=9(m)
Diện tích ban đầu là \(9\times15=135\left(m^2\right)\)

\(2x^3-6x^2=x^2-3x\)
=>\(2x^2\left(x-3\right)-x\left(x-3\right)=0\)
=>x(x-3)(2x-1)=0
=>\(\left[{}\begin{matrix}x=0\\x-3=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=\dfrac{1}{2}\end{matrix}\right.\)

đây nek bn
Bài 4. Viết các số đo sau dưới dạng số thập phân có đơn vị đo là tấn.
|
a) 21 tạ; 19 yến; 7 kg |
b) 62 tấn 5 tạ; 12 tấn 5 yến; 3 tấn 22 kg |

a: \(\dfrac{24\cdot47-23}{24+47\cdot23}\cdot\dfrac{3+\dfrac{3}{7}-\dfrac{3}{11}+\dfrac{3}{101}-\dfrac{3}{13}}{\dfrac{6}{101}-\dfrac{6}{13}+\dfrac{6}{7}-\dfrac{6}{11}+6}\)
\(=\dfrac{24\cdot\left(24+23\right)-23}{24+23\left(24+23\right)}\cdot\dfrac{3\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}{6\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}\)
\(=\dfrac{24^2+24\cdot23-23}{24+23\cdot24+23^2}\cdot\dfrac{1}{2}\)
\(=\dfrac{1105}{1105}\cdot\dfrac{1}{2}=\dfrac{1}{2}\)
b: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{19\cdot21}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{19\cdot21}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{21}\right)=\dfrac{1}{2}\cdot\dfrac{20}{21}=\dfrac{10}{21}\)

11: \(2^2\cdot3^2-5\cdot2\cdot3=6^2-30=36-30=6\)
12: \(3^2\cdot5-2^2\cdot7+1\cdot5=9\cdot5-4\cdot7+5\)
=45-28+5
=50-28=22
13: \(5^2\cdot2-3^2\cdot4=25\cdot2-9\cdot4=50-36=14\)
14: \(7^2\cdot3-5^2\cdot3=49\cdot3-25\cdot3=24\cdot3=72\)
15: \(2^3\cdot3^2-4^2\cdot3=8\cdot9-16\cdot3=72-48=24\)
16: \(5^2\cdot2^3+3^2\cdot7-8^2\cdot2\)
\(=25\cdot8+9\cdot7-64\cdot2\)
=200+63-128
=263-128=135
17: \(\left(5\cdot2^2-20\right):5+3^2\cdot6=\left(5\cdot4-20\right):5+9\cdot6\)
=0+54
=54
18: \(\left(24\cdot5-5^2\cdot2\right):\left(5\cdot2\right)-3\)
\(=\left(120-50\right):10-3\)
=7-3=4
19: \(\left[\left(5^2\cdot2^3-7^2\cdot2\right):2\right]\cdot6-7\cdot2^5\)
\(=\left[5^2\cdot2^2-7^2\right]\cdot6-7\cdot32\)
=(100-49)*6-224
=51*6-224
=82
20: \(\left(6\cdot5^2-13\cdot7\right)\cdot2-2^3\left(7+3\right)\)
\(=\left(6\cdot25-91\right)\cdot2-8\cdot10\)
\(=\left(150-91\right)\cdot2-80\)
=118-80=38

\(\left(1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3+10^3\right)\)
\(=\left(1+2+3+...+10\right)^2\)
\(=\left(\dfrac{10\cdot11}{2}\right)^2=\left(5\cdot11\right)^2=25\cdot121⋮11\)
Ta sẽ chứng minh \(1^3+2^3+3^3+...+n^3=\left[\dfrac{n\left(n+1\right)}{2}\right]^2\) bằng quy nạp. (*)
Thật vậy, với \(n=1\) thì (*) thành \(1^3=\left[\dfrac{1.2}{2}\right]^2\), luôn đúng
Giả sử (*) đúng đến \(n=k\ge1\), khi đó cần chứng minh (*) đúng với \(n=k+1\). Thật vậy, với \(n=k+1\) thì
\(VT=1^3+2^3+3^2+...+k^3+\left(k+1\right)^3\)
\(=\left[\dfrac{k\left(k+1\right)}{2}\right]^2+\left(k+1\right)^3\) (theo giả thiết quy nạp)
\(=\left(k+1\right)^2\left(\dfrac{k^2}{4}+k+1\right)\)
\(=\left(k+1\right)^2\left(\dfrac{k^2+4k+4}{4}\right)\)
\(=\dfrac{\left(k+1\right)^2\left(k+2\right)^2}{4}\)
\(=\left[\dfrac{\left(k+1\right)\left(k+2\right)}{2}\right]^2\)
Vậy (*) đúng với \(n=k+1\). Theo nguyên lí quy nạp, (*) được chứng minh.
Như vậy \(1^3+2^3+3^3+...+10^3=\left(\dfrac{10.11}{2}\right)^2=\left(5.11\right)^2=25.11^2⋮11\), ta có đpcm.
 giup mik vs
giup mik vs
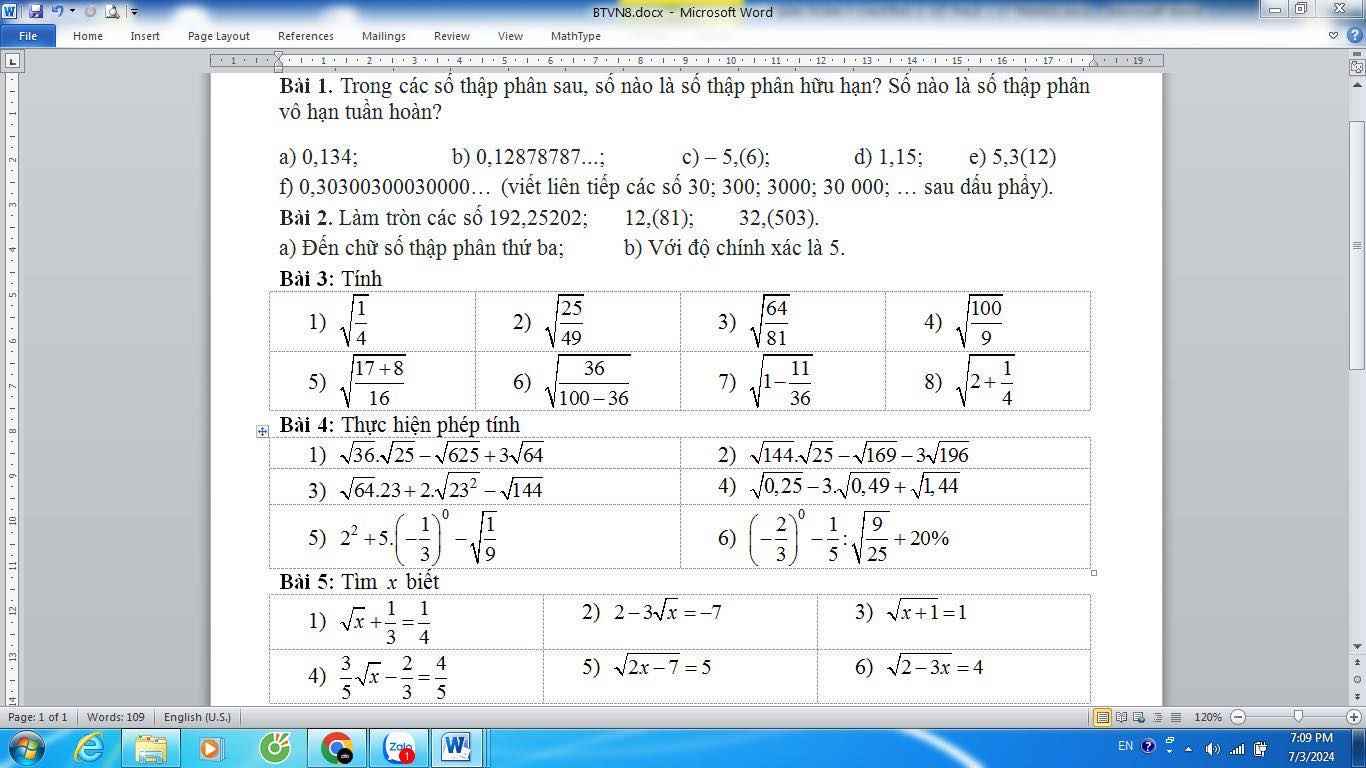
Lời giải:
Ta thấy, với $a,b,c,d>0$ thì:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}> \frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=\frac{a+b+c+d}{a+b+c+d}=1(*)$
Lại có:
Xét $\frac{a}{a+b+c}-\frac{a+d}{a+b+c+d}=\frac{-d(b+c)}{(a+b+c)(a+b+c+d)}<0$ với mọi $a,b,c,d>0$
$\Rightarrow \frac{a}{a+b+c}< \frac{a+d}{a+b+c+d}$
Tương tự: $\frac{b}{b+c+d}< \frac{b+a}{a+b+c+d}, \frac{c}{c+d+a}< \frac{c+b}{a+b+c+d}; \frac{d}{d+a+b}< \frac{d+c}{a+b+c+d}$
Cộng lại suy ra:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}< \frac{a+d+b+a+c+b+d+c}{a+b+c+d}=\frac{2(a+b+c+d)}{a+b+c+d}=2(**)$
Từ $(*); (**)\Rightarrow$ đpcm.