Lời giải:

a. $396.11\vdots 9$ vì $396\vdots 9$

b. $2.4.6...12=2.4.8.10.6.12=2.4.8.10.72\vdots 9$ do $72\vdots 9$

c. $38.127.26\not\vdots 9$ do không có thừa số nào trong 3 thừa số này chia hết cho $9$

d. $1.3.5.7\not\vdots 9$ 

2 = 2

9 = 3²

2012 = 2².503

LLàm kiểu gì

Em cần đăng đầy đủ nội dung đề bài thì cô mới giảng chi tiết cho em được em nhé.

Bài 2:

Số quyển sách Lan hơn Hồng sau khi hai bạn mua thêm:

12 + 2 - 8 = 6 (quyển)

Số sách của Lan lúc sau:

(46 + 6) : 2 = 26 (quyển)

Số sách của Hồng lúc sau

46 - 26 = 20 (quyển)

*) Nếu tính số sách lúc đầu thì:

Số sách của Lan lúc đầu:

26 - 2 = 24 (quyển)

Số sách của Hồng lúc đầu:

24 - 12 = 12 (quyển)

Bài 3:

Tổng số viên bi lúc sau:

115 + 8 + 17 = 140 (viên)

Số viên bi lúc sau mỗi hộp có:

140 : 2 = 70 (viên)

Số viên bi lúc đầu của hộp thứ nhất:

70 - 8 = 62 (viên)

Số viên bi lúc đầu của hộp thứ hai:

70 - 17 = 53 (viên)

5 em bé đi chân đất

Số em bé chỉ đeo tất là :

    5 - 3 = 2 (em)

Số em bé đi chân đất là :

    10 - 2 - 3 = 5 (em)

         Đ/s...

a) \(\dfrac{32}{40}\) = \(\dfrac{8}{10}\)

b) \(\dfrac{15}{20}\) = \(\dfrac{75}{100}\)

c) \(\dfrac{13}{125}\) = \(\dfrac{104}{1000}\)

d) \(\dfrac{552}{600}\) = \(\dfrac{92}{100}\)

a,\(\dfrac{80}{100}\)         b,\(\dfrac{75}{100}\)      c,\(\dfrac{104}{1000}\)        d,\(\dfrac{92}{100}\)

Số học sinh nam luôn không đổi

4 bạn ứng với phân số là: 

    \(\dfrac{3}{5}\) - \(\dfrac{2}{5}\) = \(\dfrac{1}{5}\) ( số học sinh nam)

Số học sinh nam là:

   4 : \(\dfrac{1}{5}\) = 20 (học sinh)

Số học sinh nữ lúc đầu là: 20 \(\times\) \(\dfrac{2}{5}\) = 8 (học sinh)

Tổng số học sinh của lớp 5 A lúc đầu là:  20+ 8 = 28 (học sinh)

đs...

B = \(\dfrac{25}{18}\) - \(\dfrac{5}{4}\) : \(\dfrac{3}{2}\) + \(\dfrac{9}{4}\) \(\times\) \(\dfrac{16}{27}\)

B =  \(\dfrac{25}{18}\) - \(\dfrac{5}{4}\) \(\times\) \(\dfrac{2}{3}\) + \(\dfrac{4}{3}\)

B = \(\dfrac{25}{18}\) - \(\dfrac{5}{6}\) + \(\dfrac{4}{3}\)

B = \(\dfrac{25}{18}\) - \(\dfrac{15}{18}\) + \(\dfrac{24}{18}\)

B = \(\dfrac{34}{18}\)

B = \(\dfrac{17}{9}\)

kết quả b=\(\dfrac{17}{9}\)bạn nhé

\(A=\dfrac{3+2\left|x+2\right|}{1+\left|x+2\right|}\)
\(=\dfrac{2+2\left|x+2\right|+1}{1+\left|x+2\right|}\)
\(=\dfrac{2\left(1+\left|x+2\right|\right)+1}{1+\left|x+2\right|}\)
\(=\dfrac{2\left(1+\left|x+2\right|\right)}{1+\left|x+2\right|}+\dfrac{1}{1+\left|x+2\right|}\)
\(=2+\dfrac{1}{1+\left|x+2\right|}\)
Ta có \(\left|x+2\right|\ge0\)
\(\Leftrightarrow1+\left|x+2\right|\ge1\)
\(\Leftrightarrow\dfrac{1+\left|x+2\right|}{1+\left|x+2\right|}\ge\dfrac{1}{1+\left|x+2\right|}\)
\(\Leftrightarrow\dfrac{1}{1+\left|x+2\right|}\le1\)
\(\Leftrightarrow2+\dfrac{1}{1+\left|x+2\right|}\le1+2=3\)
\(\Rightarrow A\le3\)
Dấu \("="\) xảy ra khi \(x+2=0\) \(\Leftrightarrow x=-2\)
Vậy giá trị lớn nhất của biểu thức \(A\) là \(3\)

A B C H D E F M K N

a/

\(BH\perp AC\Rightarrow HF\perp AC;ME\perp AC\) => ME//HF

\(AC\perp AB\Rightarrow EH\perp HF;MF\perp BH\Rightarrow MF\perp HF\) => EH//MF

=> MEHF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => ME=HF (cạnh đối hbh)

b/

\(\widehat{BMD}+\widehat{ABC}=90^o\)

\(\widehat{CME}+\widehat{ACB}=90^o\)

\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{BMD}=\widehat{CME}\)

Mà \(\widehat{CME}=\widehat{CBH}\) (góc đồng vị)

\(\Rightarrow\widehat{BMD}=\widehat{CBH}\)

Xét tg vuông DBM và tg vuông FMB có

\(\widehat{BMD}=\widehat{CBH}\) 

BM chung 

=> tg DBM = tg FMB (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)

c/

Ta có ME = HF (cmt)

tg DBM = tg FMB (cmt) => MD = BF

=> MD+ME=BF+HF=BH không đổi

d/

Từ D dựng đt // AC cắt BC tại N

\(\Rightarrow\widehat{BND}=\widehat{ACB}\) Góc đồng vị)

\(\widehat{ABC}=\widehat{ACB}\)

=> \(\widehat{BND}=\widehat{ABC}\) => tg DBN cân tại D => BD=ND (1)

tg DBM = tg FMB (cmt) => BD=MF (2)

Mà MF = EH (cạnh đối hbh) (3)

Mà EH = KC (4)

Từ (1) (2) (3) (4) => ND = KC

Mà ND//AC => ND//KC

=> DEKN là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)

Mà DK và NC là hai đường chéo của hbh cắt nhau tại trung điểm mỗi đường => trung điểm của KD nằm trên NC mà NC thuộc BC => trung điểm KD nằm trên BC

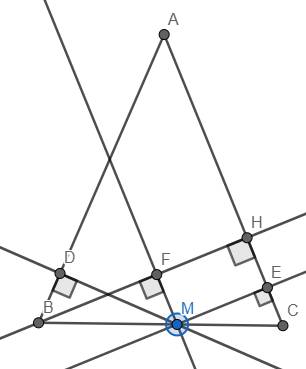
a) Vẽ MH, rõ ràng HEMF có tổng số đo của 4 góc là 360^o (vì tổng số đo của 4 góc đó là tổng số đo của các góc của các tam giác FMH và EMH)

Mà theo giả thuyết \(MD\perp AB\), \(ME\perp AC\) và \(MF\perp BH\) nên \(MF\perp ME\). Suy ra HEMF là hình chữ nhật, từ đó ME = HF.

b) Ta có \(\widehat{ABM}=\widehat{ACM}\) (vì tam giác ABC cân tại A) và \(\widehat{FMB}=\widehat{ACM}\) (vì hai góc đồng vị và AC//MF vì \(ME\perp AC\) và \(MF\perp ME\)), suy ra \(\widehat{ABM}=\widehat{FMB}\).

Xét tam giác DBM vuông tại D và FMB vuông tại F có BM là cạnh chung và \(\widehat{ABM}=\widehat{FMB}\), suy ra ΔDBM = ΔFMB (cạnh huyền - góc nhọn)

c) Từ a) và b) suy ra MD = BF, MD + ME = BF + FH = BH. Vậy khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.