Là sao ạ? Bạn có thể miêu tả kĩ hơn đc ko?

a

ta có: MN\(\perp\)AC

AB\(\perp\)AC

Do đó: MN//AB

ta có: MP\(\perp\)AB

AC\(\perp\)AB

Do đó: MP//AC

Xét ΔBMP vuông tại P và ΔMCN vuông tại N có

\(\widehat{MBP}=\widehat{CMN}\)(hai góc đồng vị, MN//AB)

Do đó: ΔBMP~ΔMCN

b: Xét ΔBAC có MP//AC

nên \(\dfrac{MP}{AC}=\dfrac{BM}{BC}\)

=>\(\dfrac{MP}{12}=\dfrac{6}{15}=\dfrac{2}{5}\)

=>\(MP=12\cdot\dfrac{2}{5}=4,8\left(cm\right)\)

Xét ΔCAB có MN//AB

nên \(\dfrac{MN}{AB}=\dfrac{CM}{CB}\)

=>\(\dfrac{MN}{9}=\dfrac{9}{15}=\dfrac{3}{5}\)

=>MN=9*3/5=5,4(cm)

Xét tứ giác APMN có \(\widehat{APM}=\widehat{ANM}=\widehat{PAN}=90^0\)

nên APMN là hình chữ nhật

=>\(AM^2=MN^2+MP^2=5,4^2+4,8^2=52,2\)

=>\(AM=\sqrt{52,2}\left(cm\right)\)

 Ta thấy một số chia hết cho 3, 4, 5 khi và chỉ khi nó chia hết cho 60.

 Số nhỏ nhất có 3 chữ số chia hết cho 60 là 120 còn số lớn nhất là 960

 Vậy có tất cả \(\left(960-120\right):60+1=15\) số có 3 chữ số chia hết cho 3, 4, 5.

Số chia hết cho 3; 4; 5 thì chia hết cho:

3 × 4 = 5 = 60

Các số có ba chữ số chia hết cho 60 là:

120; 180; 240; ...; 960

Số các số chia hết cho 3; 4; 5 là:

(960 - 120) : 60 + 1 = 15 (số)

ta có

7 giờ 36 phút= 456 phút→456 phút : 5= 91,2 phút

7 năm 19 tháng= 103 tháng⇒ 103 tháng :6= 17,1666666666666666667

7 giờ 36 phút : 5 = 1,52 giờ.               7 năm 19 tháng  : 6 = 1,43055556 năm       

\(12,6-x:\dfrac{2}{5}=\dfrac{4}{3}\times0,25\)

\(\dfrac{126}{10}-x\times\dfrac{5}{2}=\dfrac{4}{3}\times\dfrac{1}{4}\)

\(\dfrac{63}{5}-x\times\dfrac{5}{2}=\dfrac{1}{3}\)

\(x\times\dfrac{5}{2}=\dfrac{63}{5}-\dfrac{1}{3}\)

\(x\times\dfrac{5}{2}=\dfrac{184}{15}\)

\(x=\dfrac{184}{15}:\dfrac{5}{2}\)

\(x=\dfrac{184}{15}\times\dfrac{2}{5}\)

\(x=\dfrac{368}{75}\)

a) \(4x^2-1=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x\right)^2-1^2=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(4-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\4=x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=4\end{matrix}\right.\)

Vậy: ...

b) \(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)

\(\Leftrightarrow\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\)

\(\Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\)

\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)

\(\Leftrightarrow x-100=0\)

\(\Leftrightarrow x=100\)

Vậy: ... 

a) Bảng giá trị

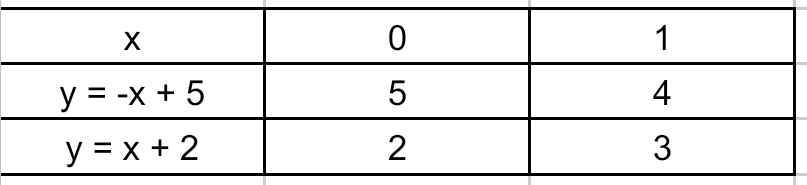  Đồ thị:

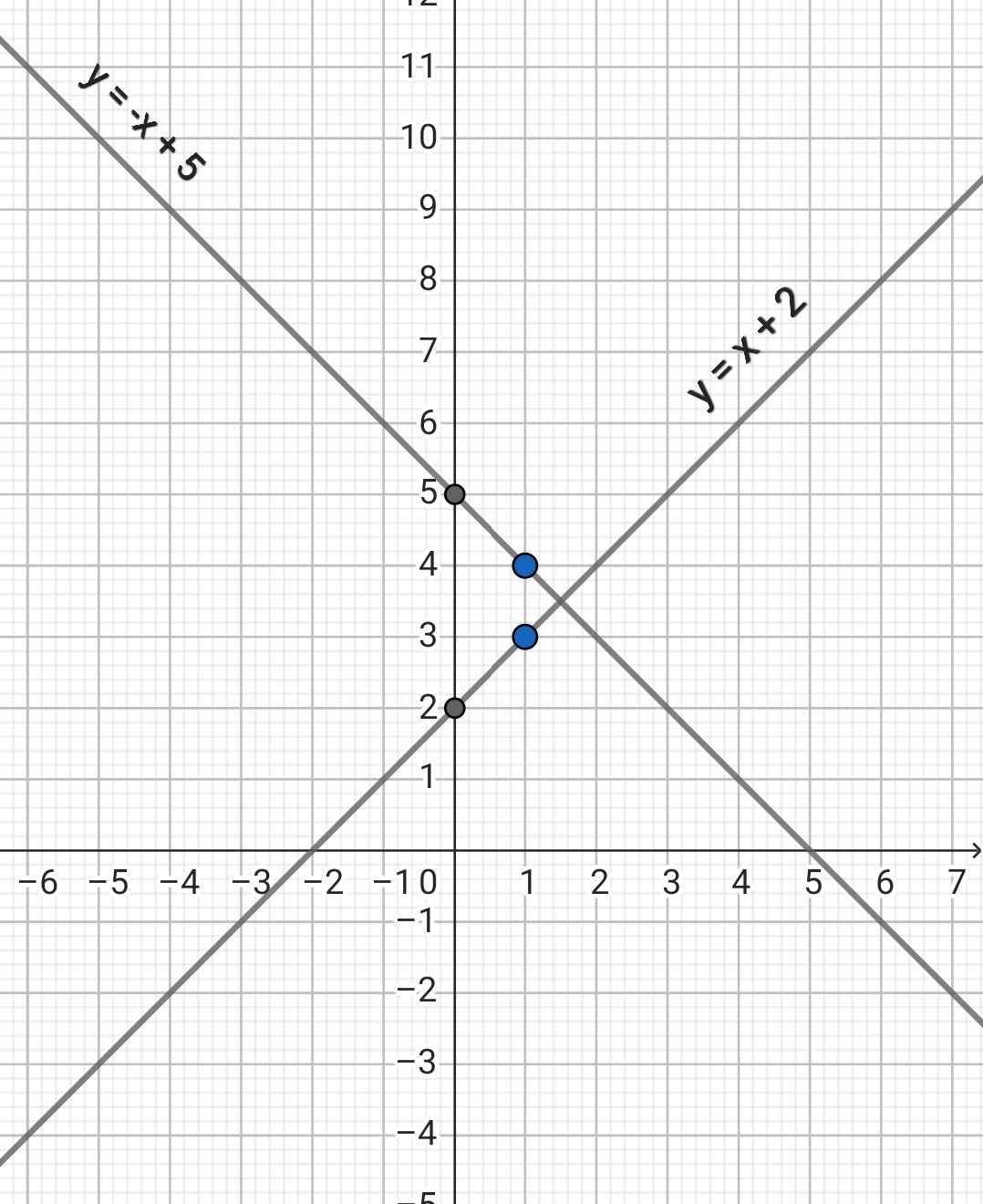
b) Phương trình hoành độ giao điểm của (d₁) và (d₂):

-x + 5 = x + 2

-x - x = 2 - 5

-2x = -3

x = 3/2

Thay x = 3/2 vào (d₂), ta có:

y = 3/2 + 2 = 7/2

Vậy tọa độ giao điểm M(3/2; 7/2)

c) Gọi (d₃): y = ax + b (a ≠ 0) là đồ thị của hàm số cần tìm

Do (d₃) // (d₁) nên a = -1

⇒ (d₃): y = -x + b

Do (d₃) đi qua K(-4; 2) nên thay tọa độ của K(-4; 2) vào (d₃), ta có:

-(-4) + b = 2

b = 2 - 4

b = -2

Vậy hàm số cần tìm là:

y = -x - 2

a) Đồ thị hs:`y=-2x+5` cắt `Ox(5/2;0)` và cắt `Oy(0;5)` 

Đồ thị hs: `y=x+2` cắt `Ox(-2;0)` và cắt `Oy(0;2)` 

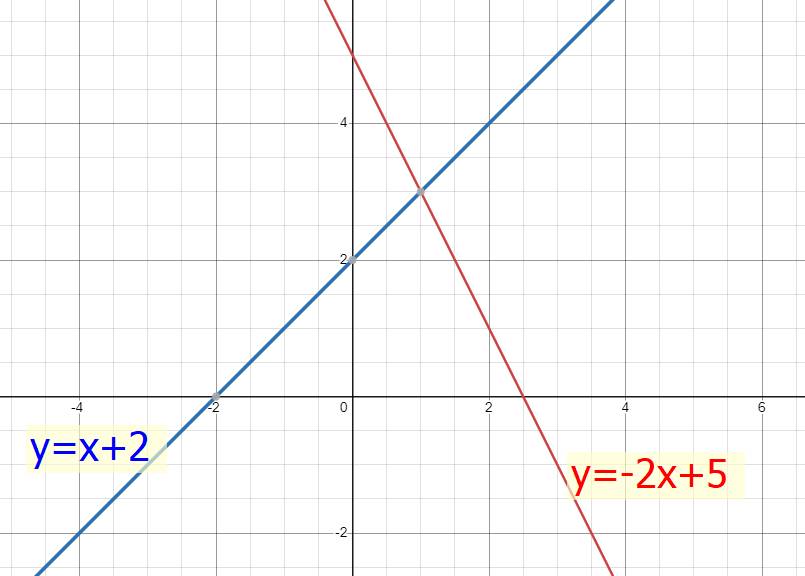
b) Ta có pt hoành độ giao điểm của (d₁) và (d₂): 

\(-2x+5=x+2\)

\(\Leftrightarrow x+2x=5-2\)

\(\Leftrightarrow3x=3\)

\(\Leftrightarrow x=1\)

Thay `x=1` vào `(d_2)` ta có: \(y=1+2=3\)

`=>M(1;3)` 

c) Hàm số `y=ax+b` có đồ thị song song với `(d_1):y=-2x+5` 

`=>a=-2` 

`=>y=-2x+b` 

Mà hàm số này đi qua điểm `K(-4;2)` ta thay `x=-4` và `y=2` vào ta có:

`2=-2*(-4)+b`

`<=>2=8+b`

`<=>b=2-8=-6` 

Vậy hàm số đó là: `y=-2x-6` 

A =  37 x 47 x 57 x ...x 187

Xét dãy số: 37; 47; 57; ...; 187

Dãy số trên là dãy số cách đều với khoảng cách là:

                 47 - 37 = 10

Số số hạng của dãy số trên là:

             (187 - 37) : 10  +  1 = 16

16 : 4 = 4

Vậy nhóm bốn thừa số liên tiếp của A thành nhóm ta được:

A =  (37 x 47 x 57 x 67) x ... (157 x 167 x 187)

A = \(\overline{..1}\) x ...\(\overline{..1}\)

A = \(\overline{..1}\)

B  = 49 x 59 x 69 x ... x269

Xét dãy số: 49; 59; 69;...; 269

Dãy số trên là dãy số cách đều với khoảng cách là: 59 - 49 = 10 

Số số hạng của dãy số trên là: (269 - 49): 10 + 1 = 23 

vì 23 : 2 = 11 dư 1 

Nhóm hai thừa số liên tiếp của B vào khi đó:

B  =(49 x 59) x (59 x 79) x ... x (249 x 259) x 269

B = \(\overline{..1}\) x \(\overline{..1}\) x \(\overline{..1}\) x... x 269

B = \(\overline{..9}\)

Sửa đề: Chiều dài đáy bể hơn chiều rộng đáy bể là 5m

Chu vi đáy bể bơi là:

225:2,5=90(m)

Nửa chu vi đáy bể bơi là 90:2=45(m)

Chiều dài đáy bể là \(\dfrac{45+5}{2}=25\left(m\right)\)

Chiều rộng đáy bể là 25-5=20(m)

Diện tích đáy bể là \(25\cdot20=500\left(m^2\right)=50000\left(dm^2\right)\)

Diện tích 1 viên gạch là \(5^2=25\left(dm^2\right)\)

Số viên gạch cần dùng là:

50000:25=2000(viên)

Chỗ 5² sửa thành 5x5 nhé

Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là x(ngày) và y(ngày)

(Điều kiện: x>0 và y>0)

Trong 1 ngày, người thứ nhất làm được: \(\dfrac{1}{x}\left(côngviệc\right)\)

Trong 1 ngày, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)

Trong 1 ngày, hai người làm được: \(\dfrac{1}{10}\left(côngviệc\right)\)

Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\left(1\right)\)

Trong 7 ngày, người thứ nhất làm được: \(\dfrac{7}{x}\)(công việc)

Trong 7+9=16 ngày, người thứ hai làm được: \(\dfrac{16}{y}\left(côngviệc\right)\)

Vì Sau 7 ngày cùng làm thì người thứ nhất đi chỗ khác, người thứ hai hoàn thành phần còn lại trong 9 ngày nên ta có:

\(\dfrac{7}{x}+\dfrac{16}{y}=1\left(2\right)\)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\\\dfrac{7}{x}+\dfrac{16}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x}+\dfrac{7}{y}=\dfrac{7}{10}\\\dfrac{7}{x}+\dfrac{16}{y}=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-\dfrac{9}{y}=-\dfrac{3}{10}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=30\\\dfrac{1}{x}=\dfrac{1}{10}-\dfrac{1}{30}=\dfrac{2}{30}=\dfrac{1}{15}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=15\\y=30\end{matrix}\right.\left(nhận\right)\)

vậy: thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là 15 ngày và 30 ngày

=>

lớp 5 chưa dùng hpt e