Bài 1. Cho đoạn thẳng AB = 9 cm, lấy C thuộc đoạn thẳng AB sao cho AC = 3 cm. Tính đoạn thẳng BC?
Bài 2.
a) Cho I là trung điểm của đoạn thẳng MN và MN = 6 cm. Tính MI và IN?
b) Cho H là trung điểm của đoạn thẳng CD và CH = 5 cm. Tính CD?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
C thuộc đoạn AB
=>C nằm giữa A và B
=>CA+CB=AB
=>CB+3=9
=>CB=6(cm)
Bài 2:
a: I là trung điểm của MN
=>\(MI=NI=\dfrac{MN}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b: H là trung điểm của CD
=>\(CD=2\cdot CH=2\cdot5=10\left(cm\right)\)
Bài 1
Vì điểm C nằm giữa A và B nên ta có :
BC=AB-AC
BC=9-3
BC=6(CM)
Vậy BC = 6cm
Bài 2
I là trung điểm của MN khi đó:
MI=NI=MN/2=6/2=3 (cm)
H là trung điểm của CD khi đó :
CD=2.CH=2.5=10 (CM)

em tham khảo nhé.
Có C nằm giữa A và B.
=>CA+CB=AB
3+��=9=>3+CB=9
��=9−3CB=9−3
��=6CB=6 (cm)
Vậy đoạn thẳng ��BC có độ dài là 66 cm.
Bài 2:
a) Có I là trung điểm của MN.
��=��=��2=62=3=>MI=IN=\(\dfrac{MN}{2}\)=\(\dfrac{6}{2}\)=3 (cm)
b) Có �H là trung điểm của ��CD.
=>CD=CH=\(\dfrac{CD}{2}\)
Mà CH=5 cm
=> CD=5.2=10 (cm)

Để x + 495 và 195 - x đều chia hết cho x và x là số tự nhiên lớn nhất thì x = ƯCLN(495; 195)
Ta có:
495 = 3².5.11
195 = 3.5.13
⇒ x = ƯCLN(495; 195) = 3.5 = 15


Sau ngày 1 thì số trang còn lại chiếm:
\(1-50\%=\dfrac{1}{2}\)(quyển sách)
Sau ngày 2 thì số trang còn lại chiếm:
\(\dfrac{1}{2}\cdot\left(1-40\%\right)=\dfrac{1}{2}\cdot\dfrac{3}{5}=\dfrac{3}{10}\)(quyển sách)
3 trang cuối cùng chiếm:
\(\dfrac{3}{10}\left(1-80\%\right)=\dfrac{3}{10}\cdot\dfrac{1}{2}=\dfrac{3}{20}\)(quyển sách)
Quyển sách có \(3:\dfrac{3}{20}=20\left(trang\right)\)

Diện tích hình chữ nhật là:
\(\dfrac{12+18}{2}\cdot10=30\cdot5=150\left(cm^2\right)\)
Chiều dài hình chữ nhật là: \(\sqrt{150:\dfrac{2}{3}}=\sqrt{150\cdot\dfrac{3}{2}}=15\left(cm\right)\)
=>Chiều rộng hình chữ nhật là \(15\cdot\dfrac{2}{3}=10\left(cm\right)\)
Chu vi hình chữ nhật là \(\left(15+10\right)\cdot2=50\left(cm\right)\)

Olm chào em, để tính trung bình cộng của ba số khi đã biết hai số thì em phải dựa và đề bài tìm nốt số còn lại. Cuối cùng cộng ba số rồi chia cho 3 được trung bình cộng của cả ba số em nhé.

a: \(\dfrac{2}{-9}\cdot\dfrac{7}{15}+\dfrac{-2}{9}\cdot\dfrac{8}{15}+1\dfrac{2}{3}\)
\(=\dfrac{-2}{9}\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+\dfrac{5}{3}\)
\(=-\dfrac{2}{9}+\dfrac{5}{3}=-\dfrac{2}{9}+\dfrac{15}{9}=\dfrac{13}{9}\)
b: \(\dfrac{3}{7}\cdot\dfrac{-9}{13}+\dfrac{3}{7}\cdot\dfrac{-4}{13}+1\dfrac{3}{7}\)
\(=\dfrac{3}{7}\left(-\dfrac{9}{13}+\dfrac{-4}{13}\right)+\dfrac{10}{7}\)
\(=-\dfrac{3}{7}+\dfrac{10}{7}=\dfrac{7}{7}=1\)

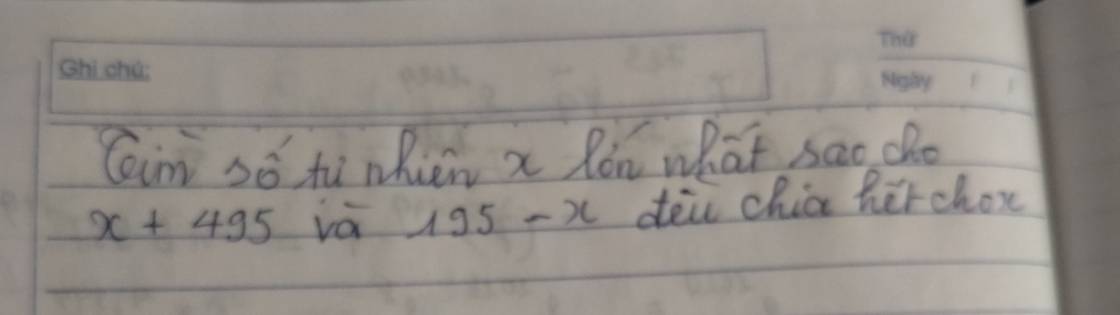
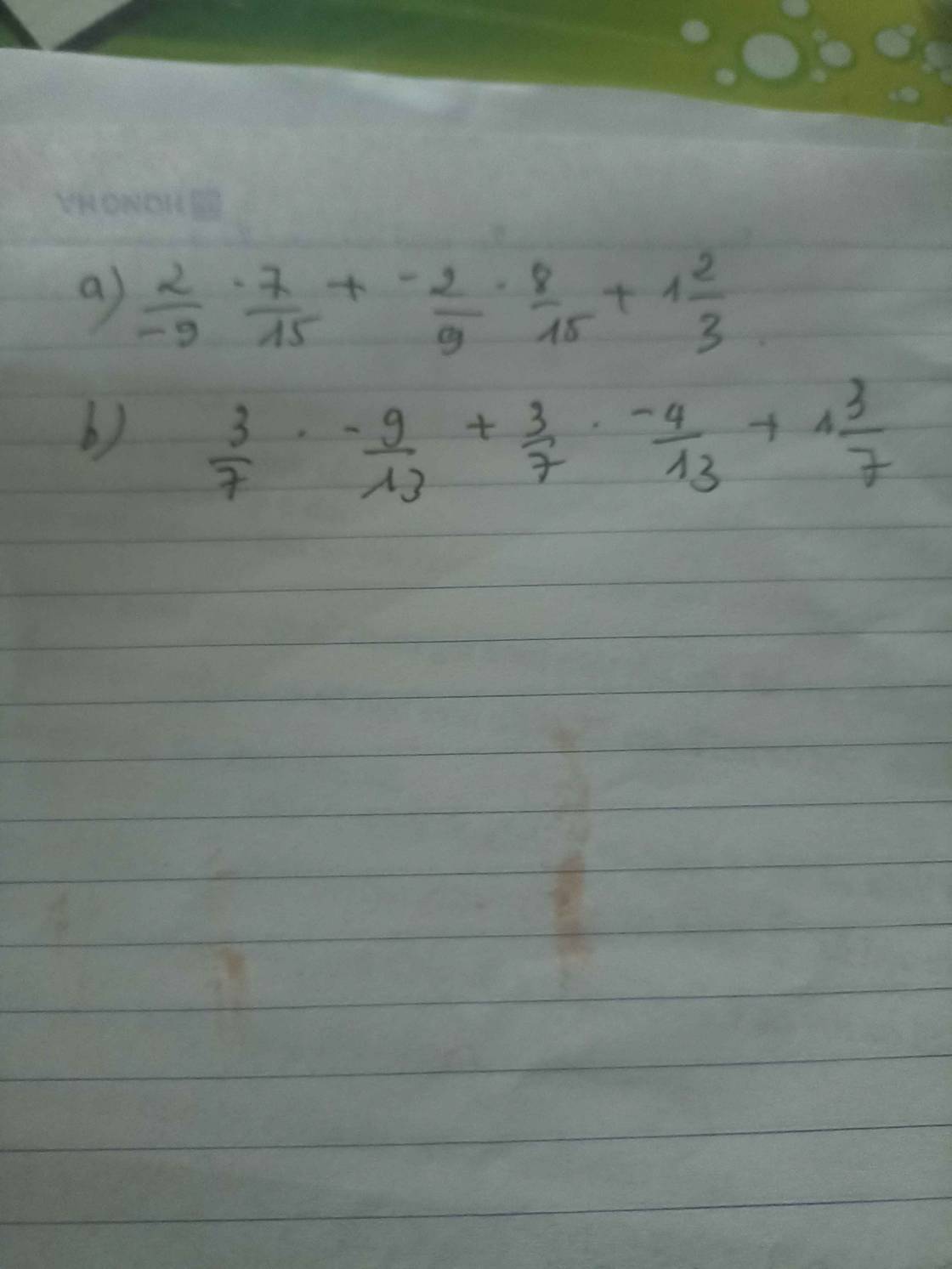
Bài 1 : Để tính đoạn thẳng BC, ta sử dụng công thức tính độ dài đoạn thẳng trong hình tam giác vuông:
Theo định lý Pythagore, ta có: AC^2 + BC^2 = AB^2 3^2 + BC^2 = 9^2 9 + BC^2 = 81 BC^2 = 81 - 9 BC^2 = 72 BC = √72 BC = 8.49 cm
Vậy đoạn thẳng BC có độ dài là 8.49 cm
Bài 2:
a) Vì I là trung điểm của đoạn thẳng MN nên MI = IN = MN/2 = 6/2 = 3 cm. Vậy MI = 3 cm và IN = 3 cm.
b) Vì H là trung điểm của đoạn thẳng CD nên CH = HD = CD/2. Ta có CH = 5 cm và HD = 5 cm, suy ra CD = CH + HD = 5 + 5 = 10 cm. Vậy đoạn thẳng CD có độ dài 10 cm.
Bài 1:
C thuộc đoạn AB
=>C nằm giữa A và B
=>CA+CB=AB
=>CB+3=9
=>CB=6(cm)
Bài 2:
a: I là trung điểm của MN
=>\(MI=NI=\dfrac{MN}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b: H là trung điểm của CD
=>\(CD=2\cdot CH=2\cdot5=10\left(cm\right)\)