Giúp mình bài 9 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


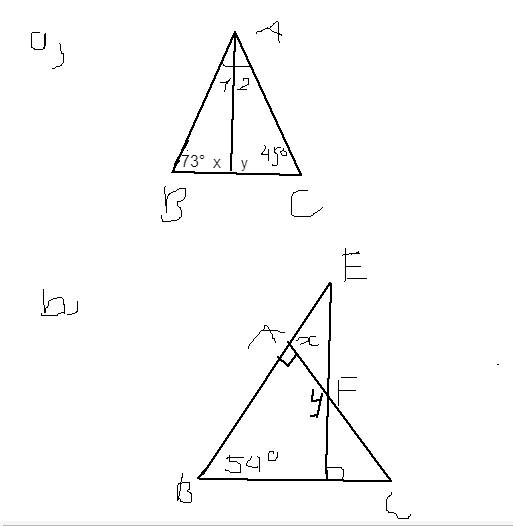
a) Ta có:
∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠BAC = 180⁰ - ∠B - ∠C
= 180⁰ - 73⁰ - 45⁰ = 62⁰
⇒ ∠A₁ = ∠A₂ = 62⁰ : 2
= 21⁰
⇒ x = 180⁰ - ∠B - ∠A₁
= 180⁰ - 73⁰ - 31⁰
= 76⁰
y = 180⁰ - ∠C - ∠A₂
= 180⁰ - 45⁰ - 31⁰
= 104⁰
b)
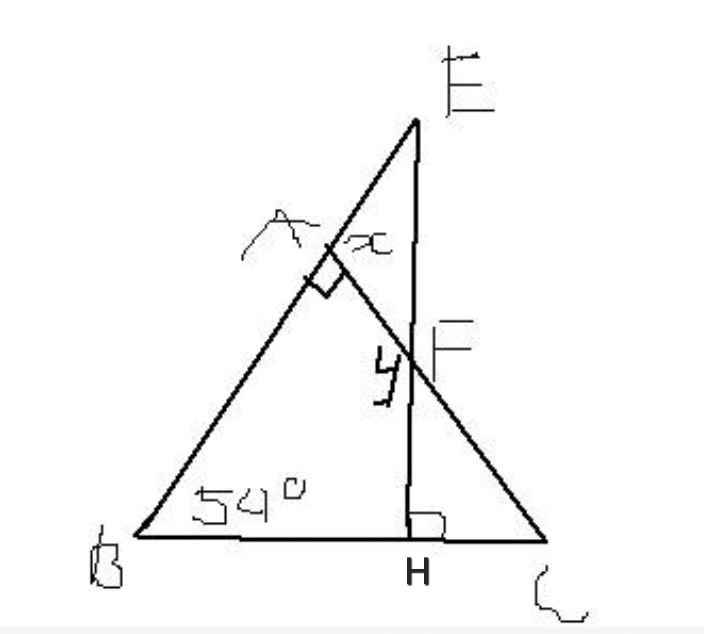
Ta có:
∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠C = 180⁰ - ∠BAC - ∠B
= 180⁰ - 54⁰ - 90⁰
= 36⁰
Ta có:
∠C + ∠CFH + ∠CHF = 180⁰ (tổng ba góc trong ∆CHF)
⇒ ∠CFH = 180⁰ - ∠C - ∠CHF
= 180⁰ - 36⁰ - 90⁰
= 54⁰
Ta có:
y + ∠CFH = 180⁰ (kề bù)
⇒ y = 180⁰ - 54⁰
= 126⁰
x là góc nào em?

\(\dfrac{5}{18}+\dfrac{7}{15}-\dfrac{7}{21}+\left(\dfrac{-10}{36}\right)+\dfrac{8}{15}+\dfrac{1}{3}-\dfrac{4}{9}\\ =\left(\dfrac{5}{18}+\dfrac{-10}{36}\right)+\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+\left(\dfrac{-7}{21}+\dfrac{1}{3}\right)-\dfrac{4}{9} \\ =0+1+0-\dfrac{4}{9}=\dfrac{5}{9}\)

b, Gọi ba số cần tìm lần lượt là:
\(x;y;z\) theo bài ra ta có:
\(\dfrac{x}{4}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{6}\);
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{z}{6}\) = \(\dfrac{x}{4}\) = \(\dfrac{z-x}{6-4}\) = \(\dfrac{4}{2}\) = 2
z = 2 x 6 = 12
\(x\) = 2 x 4 = 8
\(\dfrac{y}{5}\) = 2 ⇒ y = 2 x 5 = 10
Vậy \(x\) = 8; y = 10; z = 12
a, Gọi ba số cần tìm lần lượt là: \(x\); y; z
Theo bài ra ta có: \(\dfrac{x}{3}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{7}\); z - 2\(x\) = 11
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}\) = \(\dfrac{2x}{6}\) = \(\dfrac{z}{7}\) = \(\dfrac{z-2x}{7-6}\) = \(\dfrac{4}{1}\) = 4
\(x\) = 4x3 = 12; z = 4 x 7 = 28
\(\dfrac{y}{5}\) = 4 ⇒ y = 4x5 =20
Vậy \(x\) = 12; y = 20; z = 28

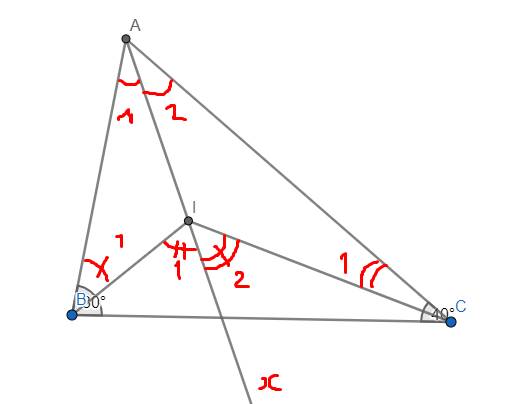
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)
\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)
\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)
\(=120^o\)
Vậy \(\widehat{BIC}=120^o\)
B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.
B2: Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB và ADC.
B3: Cho hình vẽ tính ACB

Lời giải:
$S=\frac{1}{2^2}-\frac{1}{2^4}+\frac{1}{2^6}-....+\frac{1}{2^{2002}}-\frac{1}{2^{2004}}$
$2^2S=1-\frac{1}{2^2}+\frac{1}{2^4}-....+\frac{1}{2^{2000}}-\frac{1}{2^{2002}}$
$\Rightarrow S+2^2S=1-\frac{1}{2^{2004}}<1$
$\Rightarrow 5S< 1$
$\Rightarrow S< \frac{1}{5}$
Hay $S<0,2$

2\(xy\) + 6 + \(x\) + 3 = 2024
2\(xy\) + \(x\) + 9 = 2024
2\(xy\) + \(x\) = 2024 - 9
2\(xy\) + \(x\) = 2015
\(x\).(2y + 1) = 2015
\(x\) = 2015 : (2y + 1)
\(x\in\) Z ⇒ 2y + 1 \(\in\) Ư(2015) = { 1; 5; 13; 65; 31;155; 403;2015}
Lập bảng ta có:
| 2y + 1 | 1 | 5 | 13 | 65 | 31 | 155 | 403 | 2015 |
| y | 0 | 2 | 6 | 32 | 15 | 77 | 201 | 1007 |
| \(x\) | 2015 | 403 | 155 | 31 | 65 | 13 | 5 | 1 |
| (\(x\); y) | (2015;0) | (403;2) | (155;6) | (31;32) | (65;15) | (13;77) | (5;201) | (1;1007) |



Mình đg rất cần gấp giúp mình nhé