A C B R Q P M N K J L E D H I G F 1 1 2 1

Gọi giao điểm của AJ với BC , BK với AC, CL với AB lần lượt là M, N, P

+) Từ B, C kẻ đường vuông góc với AM  lần lượt tại Q, R

Xét tam giác ADJ và tam giác CAR

có: \(\widehat{J_1}=\widehat{R_1}\left(=90^o\right)\)

AD= AC ( ACED là hình vuông)

\(\widehat{A_2}=\widehat{D_1}\)( cùng phụ góc \(\widehat{A_1}\))

=> \(\Delta ADJ=\Delta CAR\)( cạnh huyền góc nhọn)

=> AJ=CR (1)

Chứng minh tương tự : \(\Delta AIJ=\Delta BAQ\)

=> AJ= BQ (2)

Từ (1), (2) => CR=BQ

Ta  lại có: BQ//CR ( cùng vuông góc với AM)

=> \(\frac{CM}{BM}=\frac{BQ}{CR}=1\) ( vì CR =BQ, chứng minh trên)

=> CM=BM

=> M là trung điểm BC

+) Chứng minh tương tự ta được: N là trung điểm AC và P là trung điểm AB

=> AM, CP, BN là 3 đường trung tuyến của tam giác ABC đồng quy

=> AJ, BK; CL đồng quy

4,\(6x^2+10x-9x-15=6x^2+12x\) 

     \(6x^2+x-15-6x^2-12x\) =0

                11x-15=0

                 11x=15

                x=\(\frac{15}{11}\) 

vậy.......

hc tốt

\(a,\left(2x-3\right)\left(3x+5\right)+3=6x\left(x+2\right)\)

\(\Rightarrow6x^2+2x-15+3=6x^2+12x\)

\(\Rightarrow10x=-12\)

\(\Rightarrow x=-\frac{5}{7}\)

\(b,\)Sai đề không ?

TL:

a,\(-\left(x^2-2x+1\right)+1\)1

\(-\left(x-1\right)^2+1\) \(\le\) 1

=>giá trị lớn nhất của biểu thức là 1

vậy........

b,\(-\left(9x^2+6x+1\right)+20\) 

   \(-\left(3x+1\right)^2+20\) 

  \(\le20\) 

=>giá trị lớn nhất cuar biểu thức là 20

vậy.........

hc tốt

Dấu của hạng tử bậc là dấu âm nên chỉ tìm được giá trị lớn nhất thôi nhé.

a) A=2x−x2A=2x−x2+1−1A=1−(x2−2x+1)A=1−(x−1)2Do (x−1)2≥0∀x⇒A=1−(x−1)2≤1∀x Dấu “=” xảy ra khi: (x−1)2=0⇔x−1=0⇔x=1Vậy MaxA=1 khi x=1

b) B=19−6x−9x2B=20−1−6x−9x2B=20−(1+6x+9x2)B=20−(1+3x)2Do (1+3x)2≥0∀x⇒B=20−(1+3x)2≤20∀xDấu "=" xảy ra khi:(1+3x)2=0⇔1+3x=0⇔3x=−1⇔x=−13Vậy MaxB=20 khi x=−13

A B C D O 1 2 1 2 1 2

1. Xét tam giác ABD và tam giác ABC có: 

AB chung 

AD=BC ( ABCD là hình thang cân)

\(\widehat{A}=\widehat{B}\)( hai góc đối đỉnh)

=> Tam giác ABD= Tam giác ABC

2.

Ta có:  Tam giác ABD= Tam giác ABC ( theo câu 1)

=> \(\widehat{A_1}=\widehat{B_2}\)

=> Tam giác OAB cân

=> OA=OB

3. 

Ta có \(\widehat{D}=\widehat{C}\)( ABCD là hình thang cân)

=> \(\widehat{D_1}+\widehat{D_2}=\widehat{C_1}+\widehat{C_2}\)

Mà \(\widehat{D_1}=\widehat{C_1}\)( Tam giác ABD= Tam giác ABC)

=> \(\widehat{D_2}=\widehat{C_2}\)

=> Tam giác DOC cân tại O

=> DO=CO

Bài toán 8 mà sao giống toán 7 thế nhỉ?

A B C D O

a) Trong hình thang câng hai cạnh bên bằng nhau (AD = BC)

Hai góc kề ở 1 đáy bằng nhau nên theo tính chất hai đoạn thẳng song song suy ra hai góc kề ở đáy kia cũng bằng nhau.

Suy ra \(\widehat{A}=\widehat{B};\widehat{C}=\widehat{D}\)

Xét tam giác ABD và tam giác BAC có:

AD = BC (gt)

\(\widehat{A}=\widehat{B}\)

\(AB:\text{ cạnh chung }\)

\(\Rightarrow\Delta ABD=\Delta BAC\)

b) Do \(\Delta ABD=\Delta BAC\Rightarrow\widehat{DBA}=\widehat{BAC}\left(\text{hai góc tương ứng}\right)\)

\(\Rightarrow\Delta OAB\text{ cân tại O }\Rightarrow OA=OB\) (theo tính chất tam giác cân)

c) Cũng do \(\Delta ABD=\Delta BAC\Rightarrow BD=AC\Leftrightarrow OB+OD=OA+OC\)

Theo kết quả câu b ta có OA = OB suy ra OD = OC (đpcm)

Ta có

\(\left(1+\sqrt{15}\right)^2=16+2\sqrt{15}< 16+2\sqrt{16}=16+8=24\)

Ta lại có \(\sqrt{24}^2=24\)

Vậy \(1+\sqrt{15}< \sqrt{24}\)

Bài làm

Ta có: ( 1 + V15  )²  = 1 + 15 + 2 V15  = 16 + 2V15  

           V24 ² = 24 = 16 + 8

Vì V15²  = 15 < 16 = 4² 

Nên V15 < 4

=> 2V15  < 8

=> 16 + 2V15  < 24

=>  ( 1 + V15  )²  < V24 ² 

Vậy 1 + V15 < V24

# Chúc bạn học tốt #

Em tham khảo:

Câu hỏi của Thanh Triều Vương Nguyễn - Toán lớp 8 - Học toán với OnlineMath

\(\left(a+b\right).\left(b+c\right).\left(c-a\right)+\left(b+c\right).\left(c+a\right).\left(a-b\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left[\left(b+c\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left(ac-a^2+bc-ab+a^2-ab+ac-bc\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=-\left(a+b\right).2a.\left(b-c\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left(b-c\right).\left(-2a+c+a\right)=\left(a+b\right).\left(b-c\right).\left(c-a\right)\)

giai lai:

\(\left(b+c\right).\left[\left(a+b\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=-\left(b+c\right).2a.\left(b-c\right)+\left(b-c\right).\left(ac+bc+a^2+ab\right)\)

\(=\left(b-c\right).\left(-2ab-2ac+ac+bc+a^2+ab\right)\)

\(=\left(b-c\right).\left(-ab-ac+bc+a^2\right)\)

\(=\left(b-c\right).\left(a+b\right).\left(a-c\right)\)

Có PA + PC >= AC (BĐT tam giác)

PB + PD >= BD 

=>PA + PC + PB + PD >= BD + AC

Dấu ''='' xảy ra <=> P là giao điểm của AC và BD. 

Vậy...

Ban giải thích kĩ hơn được không vậy

Ta có :

MN = AB+CD2AB+CD2

=> MN là đường trung bình của tứ giác ABCD

=> MN // AB , MN// DC

=> AB // CD

Trong tứ giác ABCD , có :

AB // CD (cmt)

=> ABCD là ht (DHNB)

học tốt

Ta có:

MN=AB+CD2MN=AB+CD2

=> MN là đường trung bình

=> MN//CD;MN//AB

=> AB//CD

=> tứ giác ABCD là hình thang

học tốt

a) Ta có: AB = AD (gt)  => A thuộc đường trung trực của BD

CB = CD (gt)   => C thuộc đường trung trực của BD.

Vậy AC là đường trung trực của BD.

b) Xét ∆ ABC và ∆ADC có AB = AD (gt)

nên ∆ ABC = ∆ADC (c.c.c)

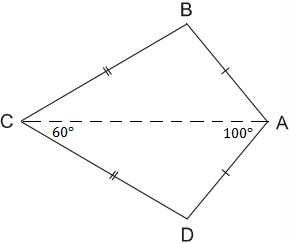
Suy ra: ⇒ˆB=ˆD

Ta có ˆB+ˆD=360⁰–(100+60)=20⁰

 Do đó ˆB=ˆD=100⁰

mban trl giúp mình câu C luôn nha ạ😭