Cho $x, \, y$ là hai số thực tùy ý. Chứng minh rằng $x^2+y^2+xy-3x-3y+3 \ge 0$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(2x-1\right)^{50}=2x-1\\ =>\left(2x-1\right)^{50}-\left(2x-1\right)=0\\ =>\left(2x-1\right)\left[\left(2x-1\right)^{49}-1\right]=0\)
TH1:
\(2x-1\\ =>2x=1\\ =>x=\dfrac{1}{2}\)
TH2:
\(\left(2x-1\right)^{49}-1=0\\=>\left(2x-1\right)^{49}=1\\ =>\left(2x-1\right)^{49}=1^{49}\\ =>2x-1=1\\ =>2x=1+1=2\\ =>x=\dfrac{2}{2}\\ =>x=1\)


\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{23}+\dfrac{1}{6}\\ =\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\dfrac{1}{23}+\dfrac{1}{6}\\ =\dfrac{1}{6}+\dfrac{1}{23}+\dfrac{1}{6}\\ =\dfrac{2}{6}+\dfrac{1}{23}\\ =\dfrac{1}{3}+\dfrac{1}{23}\\ =\dfrac{26}{69}\)

\(3^{x-1}+5\cdot3^{x-1}=162\\ =>3^{x-1}\cdot\left(1+5\right)=162\\ =>3^{x-1}\cdot6=162\\ =>3^{x-1}=162:6\\ =>3^{x-1}=27\\ =>3^{x-1}=3^3\\ =>x-1=3\\ =>x=1+3=4\)


a; 8 : \(x\) = 2
\(x\) = 8 : 2
\(x\) = 4; \(x\) \(\in\) N*
⇒ \(x\) \(\in\) A = {1; 2; 3; 4}
Tập A có 4 phần tử
b; \(x\) + 3 < 5 ⇒ \(x\) < 5 - 3 ⇒ \(x< 2\) vì \(x\in\) N
⇒ \(x\) \(\in\) B = {0; 1} Vậy tập B có 2 phần tử
C; \(x\) - 2 = \(x+2\)
\(x\) - \(x\) = 2 + 2
0 = 4 (vô lí)
C = \(\varnothing\)
Số phần tử của tập C là 0 phần tử
d; \(x:2=x:4\)
\(\dfrac{x}{2}\) - \(\dfrac{x}{4}\) = 0
\(x\) x (\(\dfrac{1}{2}\) - \(\dfrac{1}{4}\)) = 0
\(x\times\) \(\dfrac{1}{4}\) = 0
\(x=0\)
D = {0}
Tập D có 1 phần tử
e; \(x\) + 0 = \(x\)
\(x\) = \(x\)
Vậy E = {0; 1; 2; 3; 4;...}
Tập E có vô số phần tử

\(a)A\left(x\right)=x^7-3x^2-x^5+x^4-x^2+2x-7\\ =x^7-x^5+x^4-\left(3x^2+x^2\right)+2x-7\\ =x^7-x^5+x^4-4x^2+2x-7\\ B\left(x\right)=x-2x^2+x^4-x^5-x^7-4x^2-1\\ =-x^7-x^5+x^4-\left(2x^2+4x^2\right)+x-1\\ =-x^7-x^5+x^4-6x^2+x-1\)
\(b)A\left(x\right)+B\left(x\right)\\ =\left(x^7-x^5+x^4-4x^2+2x-7\right)+\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7-x^7\right)-\left(x^5+x^5\right)+\left(x^4+x^4\right)-\left(4x^2+6x^2\right)+\left(2x+x\right)-\left(7+1\right)\\ =-x^5+2x^4-10x^2+3x-8\)
\(A\left(x\right)-B\left(x\right)=\left(x^7-x^5+x^4-4x^2+2x-7\right)-\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7+x^7\right)+\left(x^5-x^5\right)+\left(x^4-x^4\right)-\left(4x^2-6x^2\right)+\left(2x-x\right)-\left(7-1\right)\\ =2x^7+2x^2+x-6\)
c) Thay x = -1 vào C(x) = A(x) + B(x) ta có:
\(C\left(x\right)=-\left(-1\right)^5+2\cdot\left(-1\right)^4-10\cdot\left(-1\right)^2+3\cdot\left(-1\right)-8\\ =-\left(-1\right)+2\cdot1-10\cdot1-3\cdot1-8\\ =1+2-10-3-8\\ =-18\)

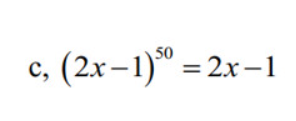
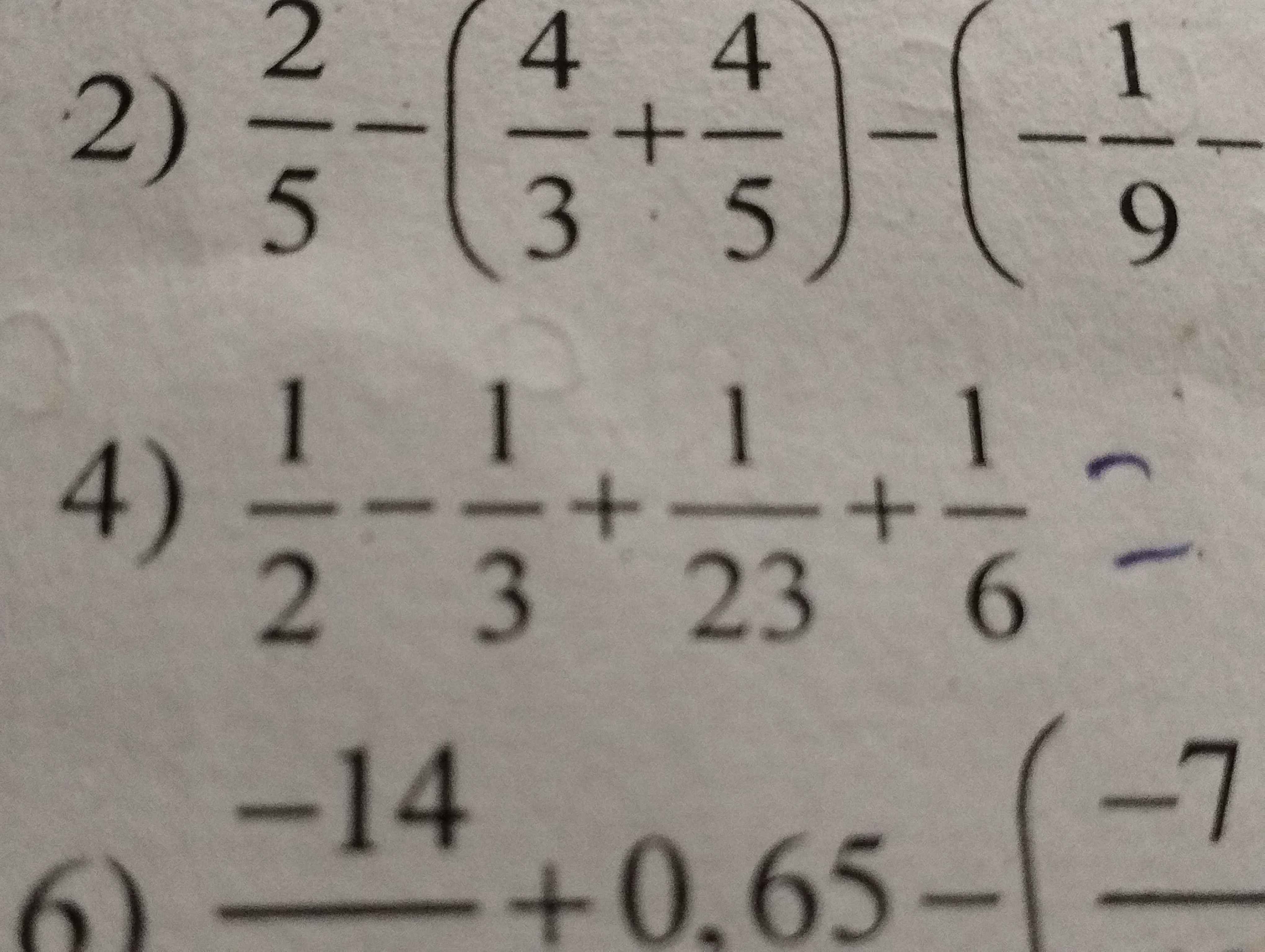
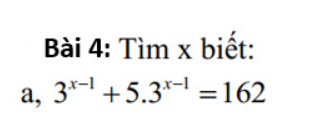

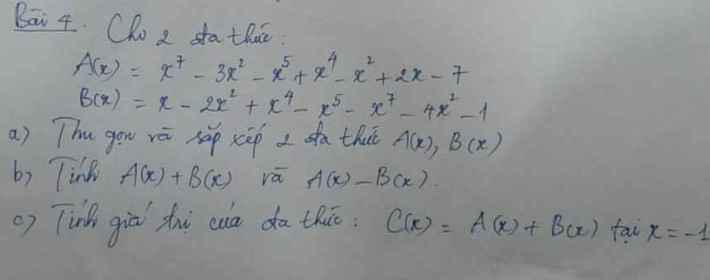
Xét \(f\left(x\right)=VT=x^2+y^2+xy-3x-3y+3\)
\(=x^2+\left(y-3\right)x+y^2-3y+3\)
Có \(\Delta=\left(y-3\right)^2-4\left(y^2-3y+3\right)\)
\(=y^2-6y+9-4y^2+12y-12\)
\(=-3y^2+6y-3\)
\(=-3\left(y-1\right)^2\le0\) với mọi \(y\inℝ\)
Mà \(f\left(x\right)\) có hệ số cao nhất bằng \(1>0\) nên từ đây có \(VT=f\left(x\right)\ge0\)
Dấu "=" xảy ra khi \(y=1\). Khi đó \(\Delta=0\) nên pt \(f\left(x\right)=0\) có nghiệm kép \(\Leftrightarrow\) \(x=\dfrac{-\left(y-3\right)}{2}=1\).
Ta có đpcm.