Cho các SN dương a, b, c thoả mãn a3 + b3 + c3 =3 x (a x b x c) và a2 = 2(b+c). Tính giá trị biểu thức T = a3 + b2023 + c (Đề Trần Mai Ninh lớp 6 bài 5 chọn đội tuyển vòng 2 năm 2024 - 2025)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề: \(\dfrac{-2}{5}\cdot\dfrac{3}{4}+\dfrac{-2}{5}\cdot\dfrac{1}{4}\)
\(=\dfrac{-2}{5}\left(\dfrac{3}{4}+\dfrac{1}{4}\right)\)
\(=-\dfrac{2}{5}\cdot\dfrac{4}{4}=-\dfrac{2}{5}\)
b: \(\left(\dfrac{5}{-3}-\dfrac{1}{2}\right)\cdot\dfrac{-6}{26}\)
\(=\left(\dfrac{-5}{3}-\dfrac{1}{2}\right)\cdot\dfrac{-3}{13}\)
\(=\dfrac{-13}{6}\cdot\dfrac{-3}{13}=\dfrac{3}{6}=\dfrac{1}{2}\)
c: \(\dfrac{-4}{15}:\left[-\dfrac{2}{3}+\dfrac{3}{5}\right]\)
\(=\dfrac{-4}{15}:\dfrac{-2\cdot5+3\cdot3}{15}\)
\(=-\dfrac{4}{15}\cdot\dfrac{15}{-1}=4\)
\(-\dfrac{2}{5}\cdot\dfrac{3}{4}+\dfrac{-2}{5}+\dfrac{1}{4}=-\dfrac{2}{5}\cdot\left(\dfrac{3}{4}+\dfrac{1}{4}\right)=-\dfrac{2}{5}\cdot\dfrac{4}{4}=-\dfrac{2}{5}\cdot1=-\dfrac{2}{5}\)
\(\left(\dfrac{5}{-3}-\dfrac{1}{2}\right)\cdot\left(-\dfrac{6}{26}\right)=\left(-\dfrac{10}{6}-\dfrac{3}{6}\right)\cdot\left(-\dfrac{6}{26}\right)=-\dfrac{13}{6}\cdot\left(-\dfrac{6}{26}\right)=\dfrac{1}{2}\)
\(-\dfrac{4}{15}:\left[\left(-\dfrac{2}{3}\right)+\dfrac{3}{5}\right]=-\dfrac{4}{15}:\left(-\dfrac{10}{15}+\dfrac{9}{15}\right)=-\dfrac{4}{15}:\left(-\dfrac{1}{15}\right)=-\dfrac{4}{15}\cdot\left(-15\right)=4\)

Đề không rõ ràng. Đề cần ghi rõ điều kiện, và yêu cầu đề. Bạn xem lại nhé.

\(\dfrac{1}{2\cdot2}+\dfrac{1}{2}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{1}{4}+\dfrac{1}{4}\cdot\dfrac{1}{5}\)
\(=\dfrac{1}{4}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}\)
\(=\dfrac{1}{4}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}\)
\(=\dfrac{1}{4}+\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{4}-\dfrac{1}{5}=\dfrac{11}{20}\)

Lời giải:
$A=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{100}{2^{100}}$
$2A=1+\frac{2}{2}+\frac{3}{2^2}+....+\frac{100}{2^{99}}$
$\Rightarrow 2A-A=1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{99}}-\frac{100}{2^{100}}$
$\Rightarrow A+\frac{100}{2^{100}}=1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{99}}$
$2(A+\frac{100}{2^{100}})=2+1+\frac{1}{2}+...+\frac{1}{2^{98}}$
$\Rightarrow 2(A+\frac{100}{2^{100}})-(A+\frac{100}{2^{100}}) = 2-\frac{1}{2^{99}}$
$\Rightarrow A+\frac{100}{2^{100}}=2-\frac{1}{2^{99}}$
$\Rightarrow A=2-\frac{1}{2^{99}}-\frac{100}{2^{100}}<2$
Bạn lưu ý lần sau viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

Lời giải:
Không mất tổng quát giả sử $a\geq b\geq c$
$\Rightarrow \frac{1}{a}\leq \frac{1}{b}\leq \frac{1}{c}$
$\Rightarrow \frac{4}{5}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\leq \frac{3}{c}$
$\Rightarrow c\leq 3,75$. Mà $c$ là stn khác 0 nên $c=1,2,3$
Nếu $c=1$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=-\frac{1}{5}<0$ (vô lý - loại)
Nếu $c=2$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=\frac{3}{10}$
Do $\frac{1}{a}\leq \frac{1}{b}$ nên $\frac{3}{10}=\frac{1}{a}+\frac{1}{b}\leq \frac{2}{b}$
$\Rightarrow b\leq 6,66$
Do $b$ là số tự nhiên và $b\geq c$ nên $b=2,3,4,5,6$
Thay vào tìm $a$ ta thấy $b=4; a=20$ và $b=5, a=10$
Nếu $c=3$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=\frac{7}{15}$
Do $\frac{1}{a}\leq \frac{1}{b}$ nên $\frac{7}{15}=\frac{1}{a}+\frac{1}{b}\leq \frac{2}{b}$
$\Rightarrow b\leq 4,28$
Mà $b$ là và $b\geq c=3$ nên $b=3;4$. Thay vào tìm $a$ thấy không thỏa mãn.
Vậy $(a,b,c)=(2,4,20), (2,5,10)$ và hoán vị.

c; \(\dfrac{x}{10}\) = \(\dfrac{-2}{5}\)
\(x\) = \(\dfrac{-2}{5}\) x 10
\(x\) = - 4
Vậy \(x\) = - 4
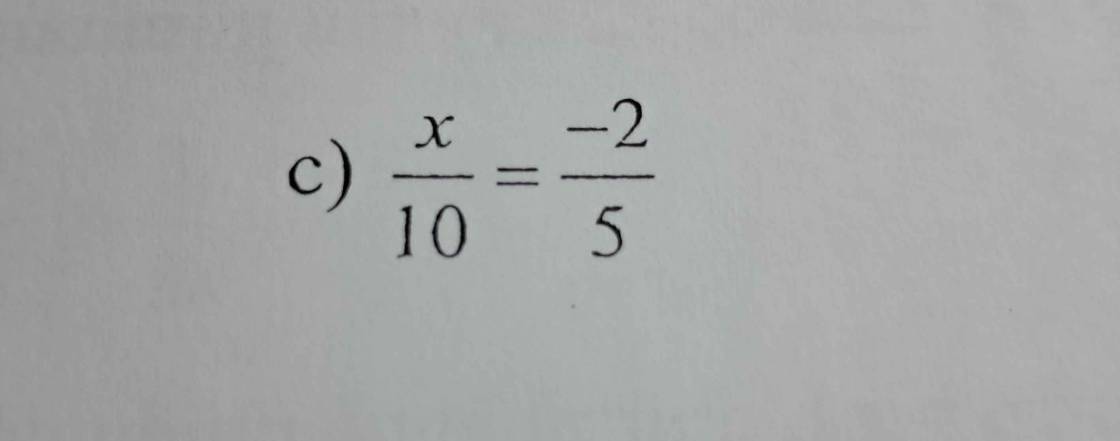
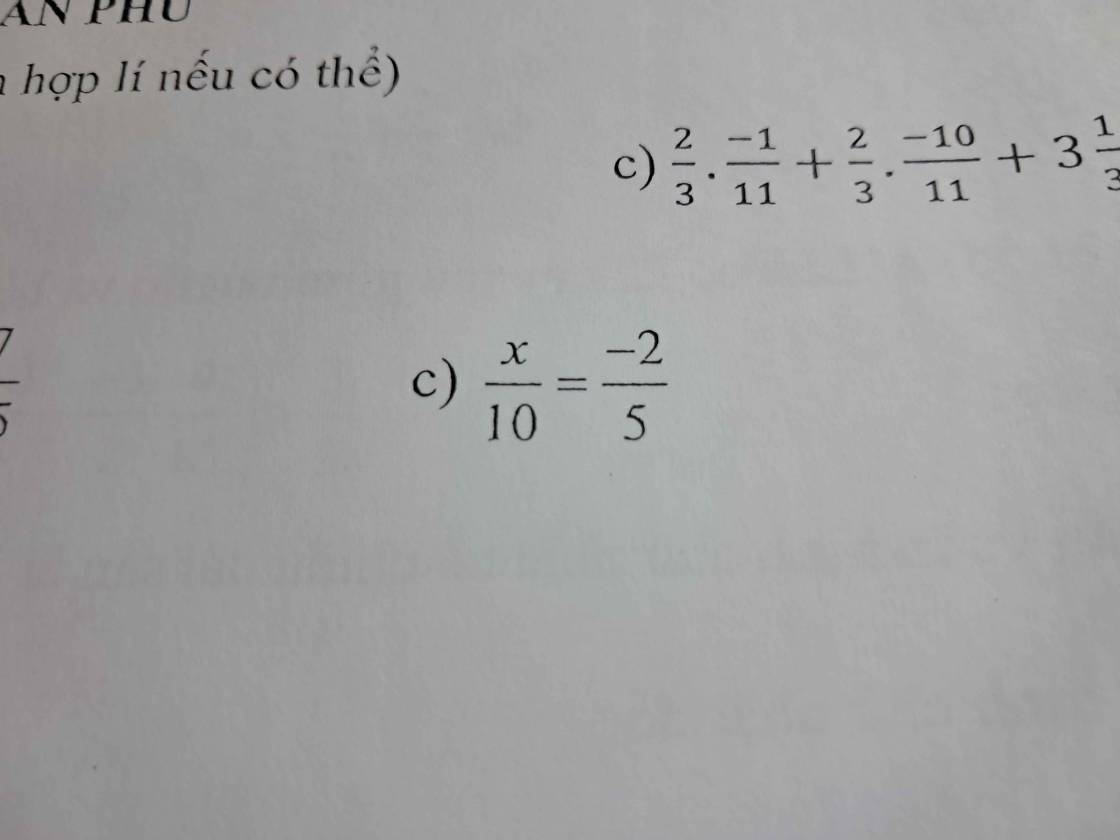
Theo Co-si, ta có:
\(a^3+b^3+c^3>=3\sqrt[3]{a^3\cdot b^3\cdot c^3}=3bac\)
Dấu '=' xảy ra khi a=b=c
\(a^2=2\left(b+c\right)\)
=>\(a^2=2\left(a+a\right)=4a\)
=>\(a^2-4a=0\)
=>a(a-4)=0
=>\(\left[{}\begin{matrix}a=0\left(loại\right)\\a=4\left(nhận\right)\end{matrix}\right.\)
Do đó: a=b=c=4
\(T=4^3+4^{2023}+4=68+4^{2023}\)
Ai giúp mình với