Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [ -20;20] để hàm số |2x³ - 3(2m+3)x² + 6m(m+3)x| đồng biến trên khoảng (0;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đề thi đánh giá năng lực
27 tháng 7 2024
\(y=\dfrac{x^2-\left(x^2+4mx+1\right)}{x+\sqrt{x^2+4mx+1}}=\dfrac{-4mx-1}{x+\sqrt{x^2+4mx+1}}\)
\(=\dfrac{-4mx-1}{x+\left|x\right|\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}\)
\(\lim\limits_{x\rightarrow\pm\infty}y\dfrac{-4m-\dfrac{1}{x}}{1\pm\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}=-4m\)
Để y = 1 là TCN => -4m = 1 => m = -1/4
NQ
Ngô Quyết
VIP
27 tháng 7 2024
Bạn chỉ cần vào lĩnh vực mà mik yêu thích để có tiến bộ thì sau đó sẽ giỏi
20 tháng 7 2024
a, Ta có (AC;AB) = ^BAC
tan^BAC = BC/AB = 1 => ^BAC = 450
b, Ta có BD // B'D'
=> (AD';BD) = (AD';B'D') = ^AD'B'
Xét tam giác AD'B' ta có AB' = B'D' = AD'
=> tam giác AD'B' đều => ^AD'B' = 600
c, Ta có BD vuông AC ; BD vuông CC'
=> BD vuông (ACC')
Mà AC' thuộc (ACC') => AC' vuông BD
4 tháng 7 2024
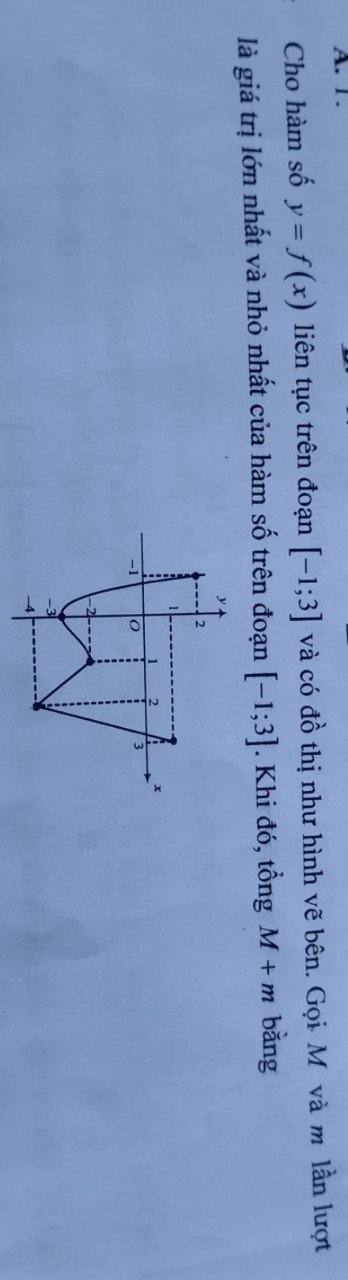
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)
và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)
Khi đó \(M+m=2-4=-2\)