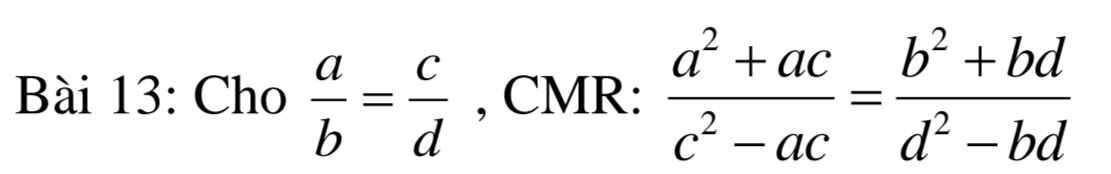 giải giúp mình với mình cần gấp ai giải đc mình tick cho
giải giúp mình với mình cần gấp ai giải đc mình tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{a}{b}=\dfrac{b}{d}=>b^2=ad\)
Ta có:
\(VT=\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a^2+ad}{ad+d^2}=\dfrac{a\left(a+d\right)}{d\left(a+d\right)}=\dfrac{a}{d}=VP\)

\(4y^4+1\\ =4y^4+4y^2+1-4y^2\\ =\left(4y^4+4y^2+1\right)-4y^2\\ =\left(2y^2+1\right)^2-\left(2y\right)^2\\ =\left(2y^2-2y+1\right)\left(2y^2+2y+1\right)\)

\(\left\{{}\begin{matrix}2x+y=-1\\3y-x=7m-10\end{matrix}\right. \Leftrightarrow\left\{{}\begin{matrix}6x+3y=-3\\-x+3y=7m-10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=-1\\7x=7-7m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\left(1-m\right)+y=-1\\x=1-m\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-1-2\left(1-m\right)=2m-3\\x=1-m\end{matrix}\right.\)
\(x^2-2y=\left(1-m\right)^2-\left(2m-3\right)\)
\(=1-2m+m^2-2m+3=m^2-4m+4\\ =\left(m-2\right)^2\)
Ta có: \(\left(m-2\right)^2\ge0\forall m=>x^2-2y\ge0\forall m\)
Dấu "=" xảy ra: \(m-2=0< =>m=2\)
Vậy: \(Min_{x^2-2y}=0< =>m=2\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{5a+3b}{5a-3b}=\dfrac{5bk+3b}{5bk-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\\ =\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5dk+3d}{5dk-3d}=\dfrac{5c+3d}{5c-3d}=VP\)

\(\dfrac{2}{15}-\dfrac{7}{10}\\ =\dfrac{4}{30}-\dfrac{21}{30}\\ =\dfrac{4-21}{30}\\ =\dfrac{-17}{30}\)

Em ơi chia hết cho 4 thì làm sao lại dư 1 được nữa em.
Gọi a là số cần tìm
Vì a chia 4 dư 1 nên a là số lẻ
Nhưng theo đề bài, a là số chẵn
nên không có số nào thỏa đề bài

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\b=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}\\ =\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(1\right)\)
\(VP=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{bd\cdot k^2}{bd}=k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)
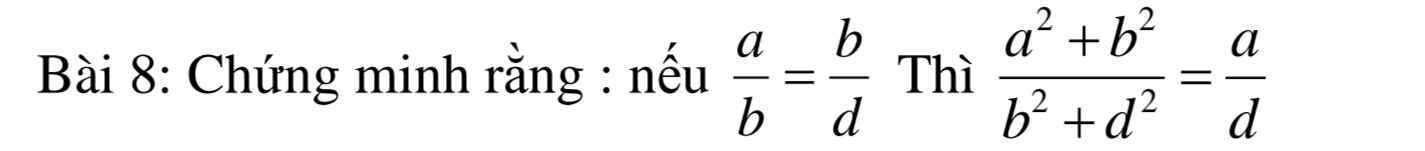


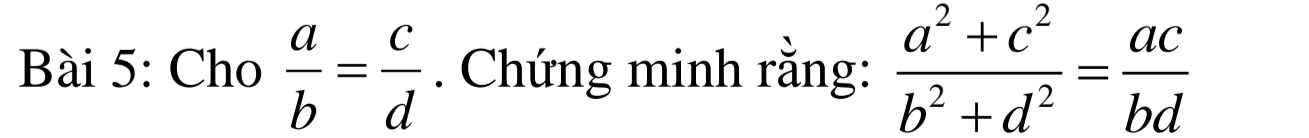
Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+ac}{c^2-ac}=\dfrac{\left(bk^2\right)+bk\cdot dk}{\left(dk\right)^2-bk\cdot dk}\\ =\dfrac{b^2k^2+bdk^2}{d^2k^2-bdk^2}=\dfrac{k^2\left(b^2+bd\right)}{k^2\left(d^2-bd\right)}=\dfrac{b^2+bd}{d^2+bd}=VP\)
VT VÀ VP LÀ J VẬY