Tìm số tự nhiên n sao cho n2 + 3n + 90 là số chính phương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các số chia hết cho 13 trong khoảng từ 1 đến 100 là: 13;26;39;52;65;78;91
=>Có 7 số

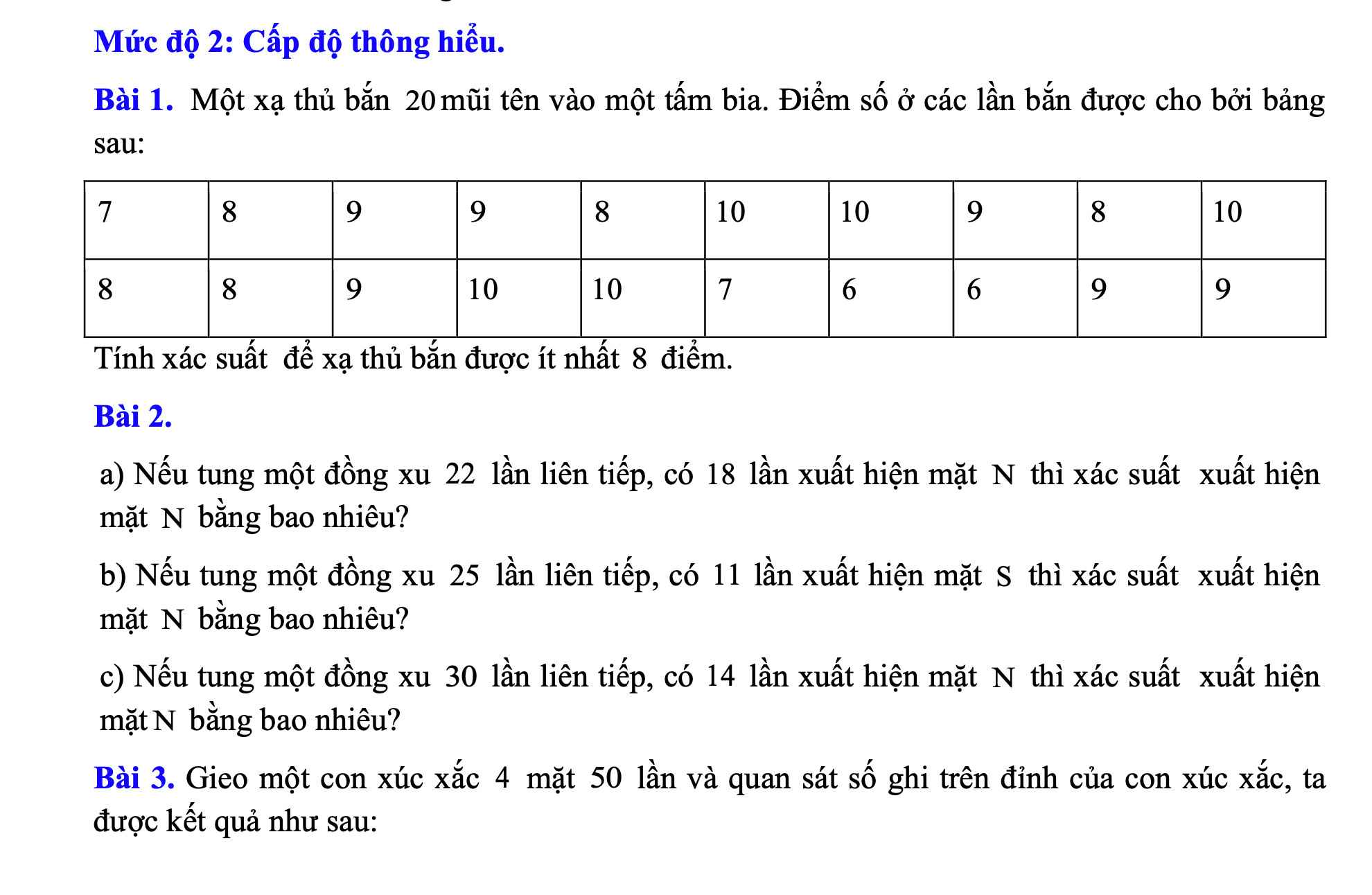
Bài 1:
Số lần bắn được ít nhất 8 điểm là:
5+6+5=16(lần)
=>Xác suất để bắn được ít nhất 8 điểm là \(P=\dfrac{16}{20}=\dfrac{4}{5}\)
Bài 2:
a: Xác suất xuất hiện mặt N là: \(\dfrac{18}{22}=\dfrac{9}{11}\)
b: Số lần xuất hiện mặt S là 25-11=14(lần)
Xác suất xuất hiện mặt S là \(\dfrac{14}{25}\)
c: Xác suất xuất hiện mặt N là \(\dfrac{14}{30}=\dfrac{7}{15}\)

\(\left(x+\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\\ < =>\left(x+\sqrt{3+x^2}\right)\left(x-\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>x^2-3-x^2\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>-\left(y+\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}\left(1\right)\)
Tương tự ta có: \(x+\sqrt{3+x^2}=-\left(y-\sqrt{3+y^2}\right)\left(2\right)\)
Lấy (1) + (2) ta có:
\(-\left(y+\sqrt{3+y^2}\right)-\left(y-\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}+x+\sqrt{3+x^2}\\ < =>-2y=2x\\ < =>2x+2y=0\\ < =>x+y=0\)

\(\left(a\right)\dfrac{5}{3}-\dfrac{1}{2}:x=\dfrac{2}{7}\\ \dfrac{1}{2}:x=\dfrac{5}{3}-\dfrac{2}{7}=\dfrac{29}{21}\\ x=\dfrac{1}{2}:\dfrac{29}{21}=\dfrac{21}{58}\\ \left(b\right)\dfrac{1}{4}\cdot x+\dfrac{7}{5}=\dfrac{5}{3}\\ \dfrac{1}{4}\cdot x=\dfrac{5}{3}-\dfrac{7}{5}=\dfrac{4}{15}\\ x=\dfrac{4}{15}:\dfrac{1}{4}=\dfrac{16}{15}\\ \left(c\right)5\cdot x-2024=3\cdot x\\ 5\cdot x-3\cdot x=2024\\ x\cdot\left(5-3\right)=2024\\ x\cdot2=2024\\ x=2024:2=1012\)

\(\dfrac{x}{8}\) + \(\dfrac{2}{3}\) = \(\dfrac{7}{6}\)
\(\dfrac{x}{8}\) = \(\dfrac{7}{6}\) - \(\dfrac{2}{3}\)
\(\dfrac{x}{8}\) = \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{1}{2}\) x 8
\(x\) = 4
\(\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\)
\(\dfrac{x}{8}=\dfrac{7}{6}-\dfrac{2}{3}\)
\(\dfrac{x}{8}=\dfrac{1}{2}=\dfrac{4}{8}\)
⇒ x = 4
Vậy x = 4

\(\overline{ab8}+\overline{ab}=949\\ \overline{ab}\times10+8+\overline{ab}=949\\\overline{ab} \times\left(10+1\right)=949-8\\ \overline{ab}\times11=941\\ \overline{ab}=941:11\\ \overline{ab}=941:11\\ \overline{ab}=\dfrac{941}{11}\)
Mà: ab là số tự nhiên nên ta loại
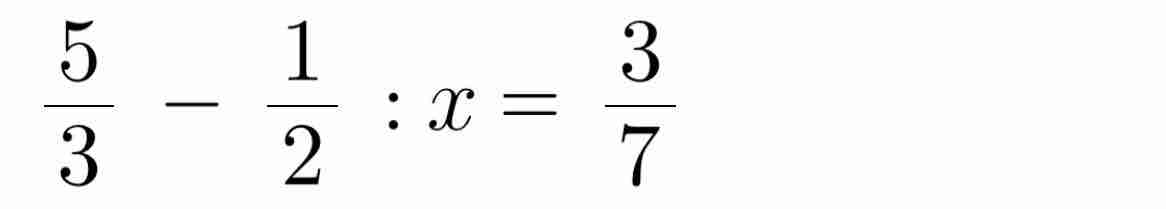
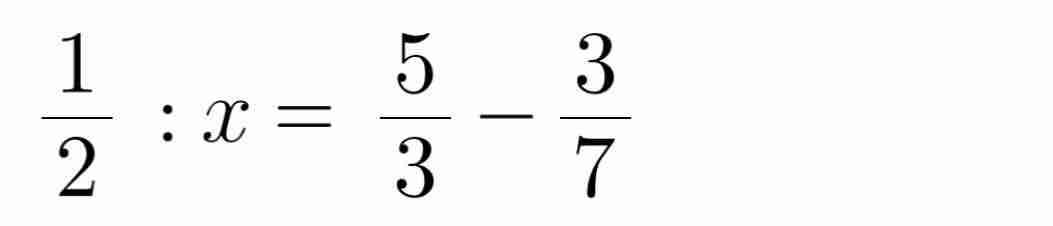
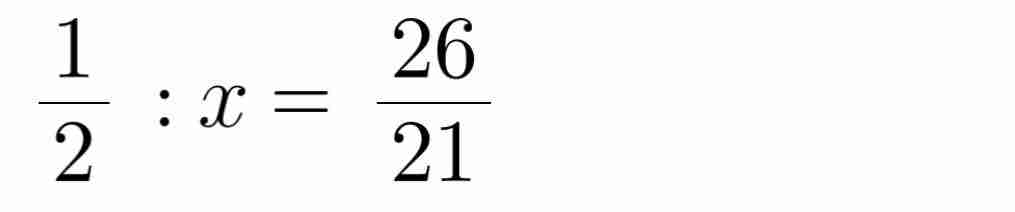

Đặt: \(n^2+3n+90=k^2\)
\(=>4n^2+12n+360=4k^2\\ =>\left(4n^2+12n+9\right)+351=4k^2\\ =>\left(2n+3\right)^2-4k^2=-351\\ =>\left(2n-2k+3\right)\left(2n+2k+3\right)=-351\)
Vì n là số tự nhiên nên: \(=>2n+2k+3>2n-2k+3\)
Ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}2n+2k+3=27\\2n-2k+3=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=2\\k=10\end{matrix}\right.\left(tm\right)\)
TH2: \(\left\{{}\begin{matrix}2n+2k+3=13\\2n-2k+3=-27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-5\\k=10\end{matrix}\right.\left(ktm\right)\)
TH3: \(\left\{{}\begin{matrix}2n+2k+3=9\\2n-2k+3=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-9\\k=12\end{matrix}\right.\left(ktm\right)\)
TH4: \(\left\{{}\begin{matrix}2n+2k+3=39\\2n-2n+3=-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=6\\k=12\end{matrix}\right.\left(tm\right)\)
TH5: \(\left\{{}\begin{matrix}2n+2k+3=3\\2n-2k+3=-117\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-30\\k=30\end{matrix}\right.\left(ktm\right)\)
TH6: \(\left\{{}\begin{matrix}2n+2k+3=117\\2n-2k+3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{57}{2}\\k=\dfrac{57}{2}\end{matrix}\right.\) (ktm)
TH7: \(\left\{{}\begin{matrix}2n+2k+3=351\\2n-2k+3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{175}{2}\\k=88\end{matrix}\right.\left(ktm\right)\)
TH8: \(\left\{{}\begin{matrix}2n+2k+3=1\\2n-2k+3=-351\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-89\\k=88\end{matrix}\right.\)
Vậy n = 2 hoặc n = 6