\(\dfrac{0,4-\dfrac{2}{9}+\dfrac{2}{11}}{1,4-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-0,25+\dfrac{1}{7}}{1\dfrac{1}{6}-0,875+\dfrac{1}{2}}\)

= \(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{2}{6}-\dfrac{2}{8}+\dfrac{2}{14}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{14}}\)

= \(\dfrac{2.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}\)

= \(\dfrac{2}{7}-\dfrac{2}{7}\)

= `0`

\(=\dfrac{2.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}{7.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}\)

\(=\dfrac{2}{7}-\dfrac{2}{7}=0\)

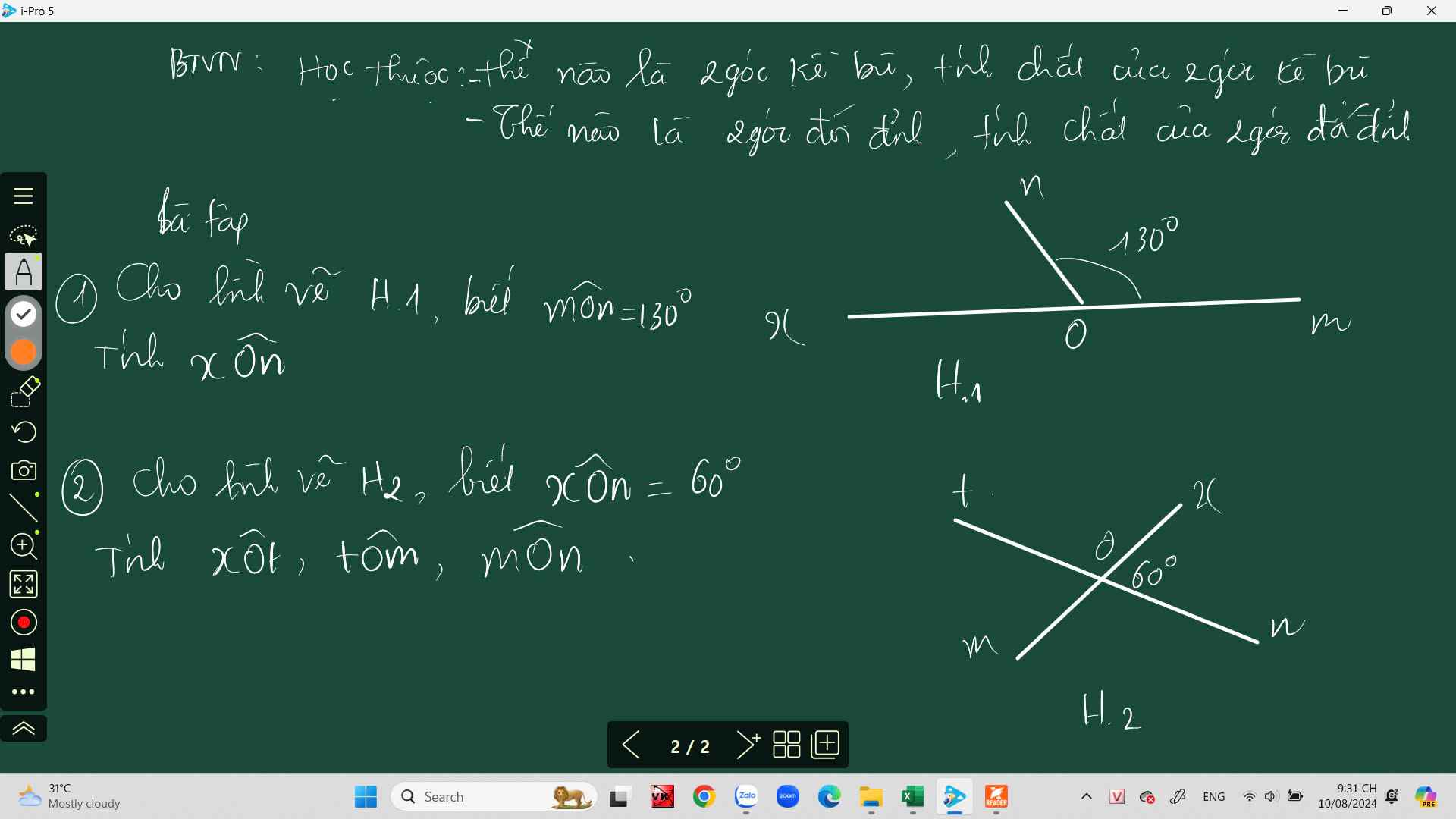
1) Ta có:

∠xOn + ∠mOn = 180⁰ (kề bù)

⇒ ∠xOn = 180⁰ - ∠mOn

= 180⁰ - 130⁰

= 50⁰

2) Ta có:

∠xOt + ∠xOn = 180⁰ (kề bù)

⇒ ∠xOt = 180⁰ - ∠xOn

= 180⁰ - 60⁰

= 120⁰

∠tOm = ∠xOn = 60⁰ (đối đỉnh)

∠mOn = ∠xOt = 120⁰ (đối đỉnh)

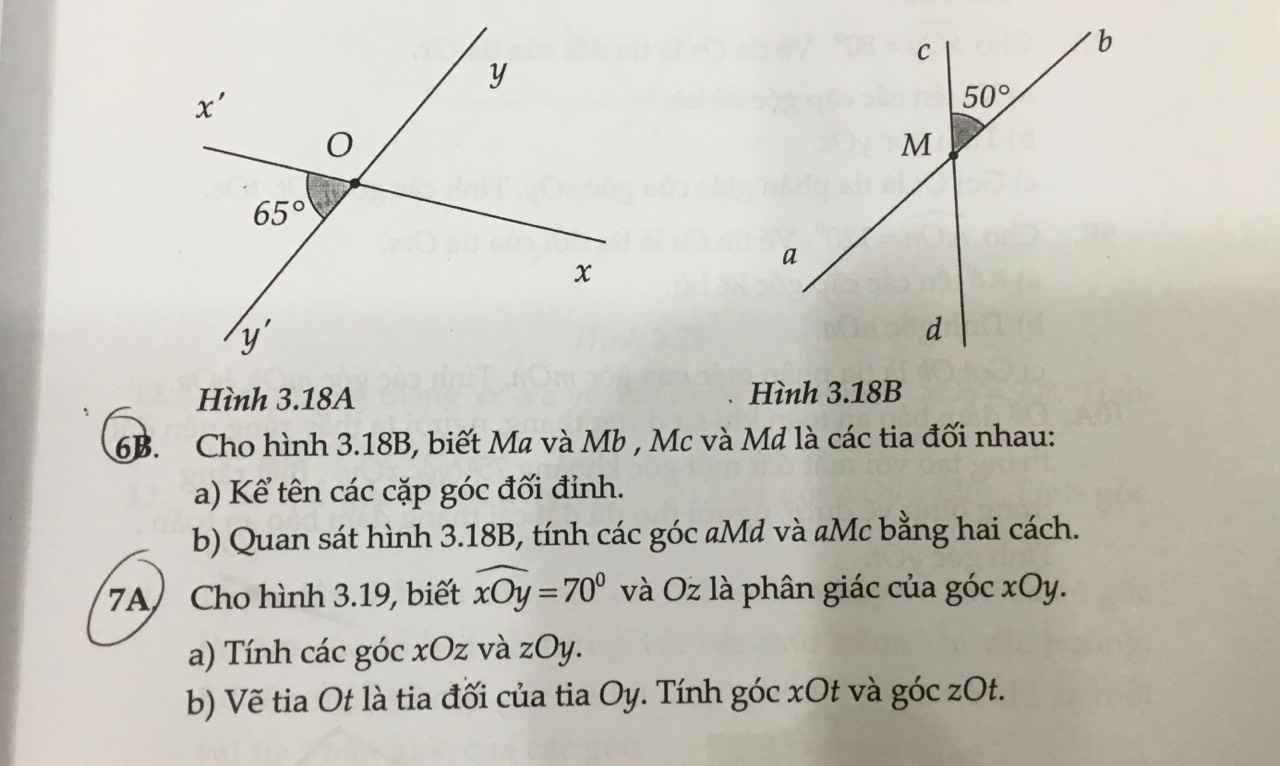
6B:

a: Các cặp góc đối đỉnh là: \(\widehat{cMb};\widehat{aMd}\); \(\widehat{aMc};\widehat{bMd}\)

b:

Cách 1: \(\widehat{aMc}+\widehat{cMb}=180^0\)(hai góc kề bù)

=>\(\widehat{aMc}=180^0-50^0=130^0\)

Ta có: \(\widehat{aMc}+\widehat{aMd}=180^0\)(hai góc kề bù)

=>\(\widehat{aMd}=180^0-130^0=50^0\)

Cách 2:

Ta có: \(\widehat{aMd}=\widehat{cMb}\)(hai góc đối đỉnh)

mà \(\widehat{cMb}=50^0\)

nên \(\widehat{aMd}=50^0\)

Ta có: \(\widehat{aMd}+\widehat{aMc}=180^0\)(hai góc kề bù)

=>\(\widehat{aMc}+50^0=180^0\)

=>\(\widehat{aMc}=130^0\)

7A:

a: Oz là phân giác của góc xOy

=>\(\widehat{xOz}=\widehat{zOy}=\dfrac{\widehat{xOy}}{2}=35^0\)

b: Ta có: \(\widehat{xOy}+\widehat{xOt}=180^0\)(hai góc kề bù)

=>\(\widehat{xOt}+70^0=180^0\)

=>\(\widehat{xOt}=110^0\)

Ta có: \(\widehat{zOt}+\widehat{zOy}=180^0\)(hai góc kề bù)

=>\(\widehat{zOt}+35^0=180^0\)

=>\(\widehat{zOt}=145^0\)

a: Xét ΔABC và ΔCDA có

AB=CD

BC=DA

AC chung 

Do đó: ΔABC=ΔCDA

=>\(\widehat{BAC}=\widehat{DCA}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD

ΔABC=ΔCDA

=>\(\widehat{BCA}=\widehat{DAC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên BC//AD

b: Xét ΔADC và ΔBCD có

AD=BC

DC chung

AC=BD

Do đó: ΔADC=ΔBCD

=>\(\widehat{ADC}=\widehat{BCD}\)

mà \(\widehat{ADC}+\widehat{BCD}=180^0\)(AD//BC)

nên \(\widehat{ADC}=\widehat{BCD}=\dfrac{180^0}{2}=90^0\)

AB//CD

=>\(\widehat{BAD}+\widehat{ADC}=180^0;\widehat{ABC}+\widehat{BCD}=180^0\)

=>\(\widehat{BAD}=180^0-90^0=90^0;\widehat{ABC}=180^0-90^0=90^0\)

\(\left(\dfrac{-5}{7}\right).\left(\dfrac{2}{5}-x\right)+\dfrac{-1}{3}=\dfrac{1}{5}+\dfrac{-3}{10}\\ \Rightarrow-\dfrac{5}{7}\cdot\dfrac{2}{5}+\dfrac{5}{7}\cdot x-\dfrac{1}{3}=\dfrac{1}{5}-\dfrac{3}{10}\\ \Rightarrow-\dfrac{2}{7}+\dfrac{5}{7}x-\dfrac{1}{3}=-\dfrac{1}{10}\\ \Rightarrow-\dfrac{13}{21}+\dfrac{5}{7}x=-\dfrac{1}{10}\\ \Rightarrow\left(\dfrac{5}{7}x\right)=-\dfrac{1}{10}+\dfrac{13}{21}\\ \Rightarrow\left(\dfrac{5}{7}x\right)=\dfrac{109}{210}\\ \Rightarrow x=\dfrac{109}{150}\)

\(a+\dfrac{2}{b}=b+\dfrac{2}{c}\Rightarrow a-b=\dfrac{2}{c}-\dfrac{2}{b}=2\left(\dfrac{b-c}{bc}\right)\)

\(\Rightarrow\dfrac{a-b}{b-c}=\dfrac{2}{bc}\)

Tương tự: \(a+\dfrac{2}{b}=c+\dfrac{2}{a}\Rightarrow\dfrac{a-c}{b-a}=\dfrac{2}{ab}\)

\(b+\dfrac{2}{c}=c+\dfrac{2}{a}\Rightarrow\dfrac{b-c}{c-a}=\dfrac{2}{ca}\)

Nhân vế với vế:

\(\left(\dfrac{a-b}{b-c}\right)\left(\dfrac{a-c}{b-a}\right)\left(\dfrac{b-c}{c-a}\right)=\dfrac{8}{\left(abc\right)^2}\)

\(\Rightarrow\left(abc\right)^2=8\)

\(\Rightarrow\left|abc\right|=2\sqrt{2}\)

Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)

=>\(\widehat{yOz}+125^0=180^0\)

=>\(\widehat{yOz}=55^0\)

\(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)...\left(\dfrac{1}{2009}-1\right)\\ =\left(\dfrac{1}{2}-\dfrac{2}{2}\right)\left(\dfrac{1}{3}-\dfrac{3}{3}\right)...\left(\dfrac{1}{2009}-\dfrac{2009}{2009}\right)\\ =\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\dfrac{-2008}{2009}\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2008}{2009}\\ =\dfrac{2\cdot3\cdot...\cdot2008}{\left(2\cdot3\cdot...\cdot2008\right)\cdot2009}\\ =\dfrac{1}{2009}\)

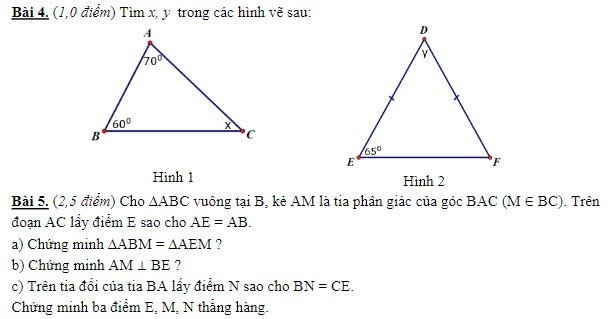
Bài 4

Hình 1: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(x+70^0+60^0=180^0\)

=>\(x=50^0\)

Hình 2: Xét ΔDEF có DE=DF

nên ΔDEF cân tại D

=>\(\widehat{EDF}=180^0-2\cdot\widehat{DEF}\)

=>\(y=180^0-2\cdot65^0=50^0\)

Bài 5:

a: Xét ΔABM và ΔAEM có

AB=AE

\(\widehat{BAM}=\widehat{EAM}\)

AM chung

Do đó: ΔABM=ΔAEM

b: ΔABM=ΔAEM

=>MB=ME

=>M nằm trên đường trung trực của BE(1)

Ta có: AB=AE

=>A nằm trên đường trung trực của BE(2)

Từ (1),(2) suy ra AM là đường trung trực của BE

=>AM\(\perp\)BE

c: Xét ΔMBN vuông tại B và ΔMEC vuông tại E có

MB=ME

BM=EC

Do đó: ΔMBN=ΔMEC

=>\(\widehat{BMN}=\widehat{EMC}\)

mà \(\widehat{EMC}+\widehat{EMB}=180^0\)(hai góc kề bù)

nên \(\widehat{BMN}+\widehat{BME}=180^0\)

=>E,M,N thẳng hàng

|x|=|y|

mà x>0; y<0

nên x=-y

2x+y=-2y+y=-y

\(\left|x\right|=\left|y\right|\) và \(x>0;y< 0\)

\(\Rightarrow y=-x\)

\(\Rightarrow2x\pm x=x\)

Vậy \(2x+y=x\)