Phân số chỉ số bánh cất đi trong tủ lạnh so với số bánh cửa hàng đã nhận là:

\(100\%-12,5\%=87,5\%=\dfrac{7}{8}\left(tổng.số.bánh\right)\)

Phân số chỉ số bánh còn lại ở ngoài sau bán được với số bánh ban đầu là:

\(\dfrac{7}{8}:10=\dfrac{7}{80}\left(tổng.số.bánh\right)\)

Phân số chỉ 3 cái bánh đã bán so với số bánh ban đầu là:

\(\dfrac{1}{8}-\dfrac{7}{80}=\dfrac{3}{80}\left(tổng.số.bánh\right)\)

Lúc đầu cửa hàng đã nhận về:

\(3:\dfrac{3}{80}=80\left(cái.bánh\right)\)

Lúc đầu sọt thứ nhất có số cam = 3/4 sọt thứ hai tức là sọt thứ nhất = 3/7 số cam

Sau khi chuyển 5 quả ở sọt thứ nhất sang sọt thứ hai thì sọt thứ nhất có số cam = 2/3 sọt thứ 2 tức là sọt thứ nhất có số cam = 2/5 tổng số cam

5 quả cam tương ứng với:

3/7 - 2/5 = 1/35 ( tổng số cam) 

Có tất cả số quả cam là:

5 : 1/35 = 175 (quả)

Số cam sọt thứ nhất là:

175 x 3/7 = 75 (quả)

Số cam sọt thứ hai là:

175 - 75 = 100 (quả)

A = \(\dfrac{2008}{2009+2010+2011}+\dfrac{2009}{2009+2010+2011}+\dfrac{2010}{2009+2010+2011}\)

Ta có: 

\(\dfrac{2008}{2009}>\dfrac{2008}{2009+2010+2011}\)

\(\dfrac{2009}{2010}>\dfrac{2009}{2009+2010+2011}\)

\(\dfrac{2010}{2011}>\dfrac{2010}{2009+2010+2011}\)

Từ 3 điều trên suy ra : A < B

sau đây là phần chữa của mình: 

\(=\dfrac{1}{2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\)

\(=\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

 \(=\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{10}\)

= \(\dfrac{3}{10}\)

= \(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\)

\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

= \(\dfrac{1}{2}-\dfrac{1}{10}\)

= \(\dfrac{2}{5}\)

(y - \(\dfrac{1}{2}\)) : \(\left(\dfrac{1}{2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\right)\)= \(\dfrac{1}{3}\)

(y\(-\dfrac{1}{2}\)): \(\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)= \(\dfrac{1}{3}\)

\(\left(y-\dfrac{1}{2}\right):\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{10}\right)=\dfrac{1}{3}\)

\(\left(y-\dfrac{1}{2}\right):\dfrac{3}{10}=\dfrac{1}{3}\)

\(\left(y-\dfrac{1}{2}\right)=\dfrac{1}{10}\)

y = \(\dfrac{3}{5}\)

Ta có : 

\(A=\dfrac{2019\times2020}{2019\times2020+1}=\dfrac{2019\times2020+1-1}{2019\times2020+1}=1-\dfrac{1}{2019\times2020+1}\)

Suy ra  A < 1 (1) 

Lại có \(B=\dfrac{2020}{2019}=\dfrac{2019+1}{2019}=\dfrac{2019}{2019}+\dfrac{1}{2019}=1+\dfrac{1}{2019}\)

Suy ra B > 1 (2) 

Từ (1) và (2) ta có : A < 1 < B

=> A < B

Vậy A < B  

Nếu dời dấu phẩy của số X sang trái 2 hàng thì được số Y 

nên số X gấp 100 lần số  Y

Nếu dời dấu phẩy của số X sang phải hai hàng thì được số Z 

nên số Z gấp 100 lần số X 

Cho số Y là 1 phần thì số X có 100 phần và số Z có: 10000 phần 

Tổng số phần là: 

1 + 100 + 100 00 = 10101 ( phần ) 

Số X là: 4928,17689 : 10101 x 100 = 48,789

Đáp số: 48,789

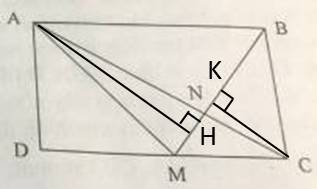
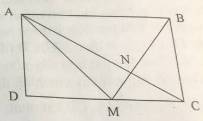
a) MC = 2/5 DC nên DC = 5/2 MC = 5/2 . 10 = 25 cm.

Do đó, AB = CD = 25 cm.

Hình thang ABCM có hai đáy AB, CM và chiều cao BC = AD = 21 cm.

Diện tích hình thang ABCM bằng: (25 + 10) x 21 : 2 = 367,5 (cm²)

b) Hạ AH \(\perp\) BM, CK \(\perp\) BM.

Ta có \(\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{AB}{MC}=\dfrac{5}{2}\) (vì cùng chiều cao, tỉ lệ diện tích bằng tỉ lệ hai đáy), do đó \(\dfrac{AH}{CK}=\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{5}{2}\) (chung đáy, tỉ lệ diện tích bằng tỉ lệ hai chiều cao)

\(\dfrac{S_{AMN}}{S_{CMN}}=\dfrac{AH}{CK}=\dfrac{5}{2}\Rightarrow\dfrac{S_{CMN}}{S_{AMC}}=\dfrac{2}{7}\)

\(S_{AMC}=\dfrac{1}{2}\times AD\times MC=\dfrac{1}{2}\times21\times10=105\left(cm^2\right)\)

\(S_{CMN}=\dfrac{2}{7}\times105=30\left(cm^2\right)\)

Diện tích giếng nước là: \(0,7\times0,7\times3,14=1,5386(m^2)\)

Diện tích của thành giếng đó là:

   \(1,5386-(0,7-0,3)\times(0,7-0,3)\times3,14=1,0352(m^2)\)