Ta có :

\(\frac{-1}{3}=\frac{-16}{48}\)     ;  \(\frac{-1}{4}=\frac{-12}{48}\)

Ba phân số xen giữa \(\frac{-1}{3}\)và \(\frac{-1}{4}\)là : \(\frac{-13}{48}\); \(\frac{-14}{48}\); \(\frac{-15}{48}\)

Ta có:

\(-\frac{1}{3}=-\frac{16}{48};-\frac{1}{4}=-\frac{12}{48}\)

Ba số hữu tỉ xem giữa là: 

\(-\frac{13}{48};-\frac{14}{48};-\frac{15}{48}\)

Vậy ba số hữu tỉ xen giữa là:
\(-\frac{13}{48};-\frac{14}{48};-\frac{15}{48}\)
 

6844464-481444.7/8-9=/

A= \(\frac{2}{5}+(\frac{-4}{3})+(\frac{-1}{2})\)

A = \(\frac{12}{30}+(\frac{-40}{30})+(\frac{-15}{30})\)

A= \(\frac{12}{30}+\frac{-55}{30}\)

A = \(\frac{-43}{30}\)

Bạn tự vẽ hình nhé

                                                                                       Giải

Ta có : \(\Delta FHI\)cân tại F ( gt ) ; FK là đường trung tuyến \(\Delta FHI\) ( gt )

\(\Rightarrow\)FK đồng thời là đường cao \(\Delta FHI\) ( t/c tam giác cân )

\(\Rightarrow\)FK \(\perp\) HI 

\(\Rightarrow\)\(\Delta FIK\)là tam giác vuông tại K 

Mà FK là trung tuyến => HK = KI = \(\frac{HI}{2}\) = 18 cm

Xét \(\Delta FIK\) vuông tại K ( cmt ) , có :

FI² = FK² + KI² ( đ/l Py-ta-go )

=> FI² = 24² + 18²

=> FI² = 576 + 324

=> FI² = 900

=> FI = 30 cm ( FI > 0 ) 

Vậy độ dài cạnh FI là 30 cm ( đpcm )

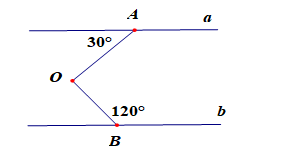
Kẻ tia \(Ox\)song song với \(a\)và \(b\).

Khi đó: \(\widehat{OAy}=\widehat{AOx}\)(hai góc so le trong bằng nhau) 

\(\widehat{BOx}+\widehat{OBz}=180^o\)(hai góc trong cùng phía bù nhau) 

\(\Leftrightarrow\widehat{BOx}=180^o-\widehat{OBz}=180^o-120^o=60^o\)

suy ra \(\widehat{AOB}=\widehat{AOx}+\widehat{BOx}=30^o+60^o=90^o\).

\(\frac{x}{3}=\frac{y}{5}=t\Leftrightarrow\hept{\begin{cases}x=3t\\y=5t\end{cases}}\).

\(A=\frac{5x^2+3y^2}{10x^2-3y^2}=\frac{5.\left(3t\right)^2+3.\left(5t\right)^2}{10.\left(3t\right)^2-3.\left(5t\right)^2}=\frac{120t^2}{15t^2}=8\)

Đáp số : 1,4 tạ .

#HT#

đáp số là 1,4 tạ à

a. Vì Ay // BC => góc yAC = góc ACB (sole trong)

                        góc yAx = góc ABC (đòng vị) 

Mà góc ABC = góc ACB => góc yAC = góc yAx => Ay là phân giác góc CAx

b. Vì AD là phân giác góc trong BAC , Ay là phân giác góc ngoài CAx 

=> Ay vuông góc với AD ( tính chất phân giác trong và ngoài )

Mà Ay // BC => góc yAD = góc ADB ( sole trong) => AD vuông góc với BC

#HT#

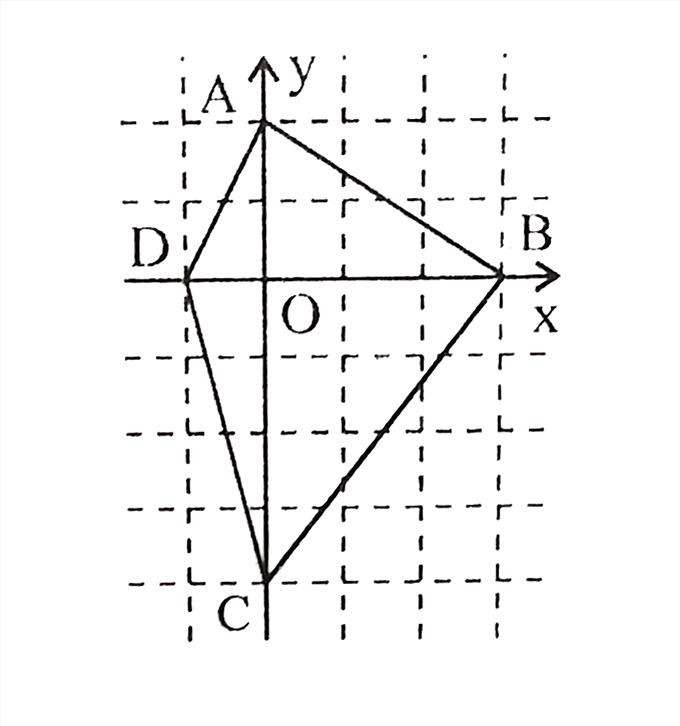
a, Áp dụng định lí Py - ta - go vào tam giác AOB vuông tại O, có:

AB² = AO² + OB²

AB² = 2² + 3²

AB² = 4 + 9

AB² = 13

AB = \(\sqrt{13}\) (cm

b,  Áp dụng định lí Py - ta - go vào tam giác BOC vuông tại O, có:

BC² = OC² + OB²

BC² = 4² + 3²

BC² = 16 + 9

BC² = 25

BC = \(\sqrt{25}\)

BC = 5 ( cm )

c,  Áp dụng định lí Py - ta - go vào tam giác COD vuông tại O, có:

CD² = OC² + OD²

CD² = 4² + 1²

CD² = 16 + 1

CD² = 17

CD = \(\sqrt{17}\)(cm)

d,  Áp dụng định lí Py - ta - go vào tam giác AOD vuông tại O có:

DA² = AO² + DO²

DA² = 2² + 1²

DA² = 4 + 1

DA² = 5

DA = \(\sqrt{5}\)(cm)

Giải:

Gọi ba số được chia lần lượt là a, b và c

Theo đề ra, ta có:

a+b+c=230a+b+c=230

Và ⎧⎪ ⎪⎨⎪ ⎪⎩a.13=b.12a.15=c.17⇔⎧⎪ ⎪⎨⎪ ⎪⎩a3=b2a5=c7⇔⎧⎪ ⎪⎨⎪ ⎪⎩a15=b10a15=c21⇔a15=b10=c21{a.13=b.12a.15=c.17⇔{a3=b2a5=c7⇔{a15=b10a15=c21⇔a15=b10=c21

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a15=b10=c21=a+b+c15+10+21=23046=5a15=b10=c21=a+b+c15+10+21=23046=5

⇔⎧⎪⎨⎪⎩a=15.5b=10.5c=21.5⇔⎧⎪⎨⎪⎩a=75b=50c=105⇔{a=15.5b=10.5c=21.5⇔{a=75b=50c=105

Vậy ...

Giải:

Gọi ba số được chia lần lượt là a, b và c

Theo đề ra, ta có:

a+b+c=230a+b+c=230

Và ⎧⎪ ⎪⎨⎪ ⎪⎩a.13=b.12a.15=c.17⇔⎧⎪ ⎪⎨⎪ ⎪⎩a3=b2a5=c7⇔⎧⎪ ⎪⎨⎪ ⎪⎩a15=b10a15=c21⇔a15=b10=c21{a.13=b.12a.15=c.17⇔{a3=b2a5=c7⇔{a15=b10a15=c21⇔a15=b10=c21

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a15=b10=c21=a+b+c15+10+21=23046=5a15=b10=c21=a+b+c15+10+21=23046=5

⇔⎧⎪⎨⎪⎩a=15.5b=10.5c=21.5⇔⎧⎪⎨⎪⎩a=75b=50c=105⇔{a=15.5b=10.5c=21.5⇔{a=75b=50c=105

Vậy ...Giải:

Gọi ba số được chia lần lượt là a, b và c

Theo đề ra, ta có:

a+b+c=230a+b+c=230

Và ⎧⎪ ⎪⎨⎪ ⎪⎩a.13=b.12a.15=c.17⇔⎧⎪ ⎪⎨⎪ ⎪⎩a3=b2a5=c7⇔⎧⎪ ⎪⎨⎪ ⎪⎩a15=b10a15=c21⇔a15=b10=c21{a.13=b.12a.15=c.17⇔{a3=b2a5=c7⇔{a15=b10a15=c21⇔a15=b10=c21

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a15=b10=c21=a+b+c15+10+21=23046=5a15=b10=c21=a+b+c15+10+21=23046=5

⇔⎧⎪⎨⎪⎩a=15.5b=10.5c=21.5⇔⎧⎪⎨⎪⎩a=75b=50c=105⇔{a=15.5b=10.5c=21.5⇔{a=75b=50c=105

Vậy ...

Gọi 3 phần lần lượt là: a ; b và c.

- Ta có: a + b + c = 230

A là:

\(\frac{1}{3}\)x  \(\frac{1}{5}\) =  \(\frac{1}{15}\)=>   \(\frac{a}{15}\)

B là:

\(\frac{1}{2}\) x   \(\frac{1}{5}\) =  \(\frac{1}{10}\) =>  \(\frac{b}{10}\)

C là:

\(\frac{1}{3}\) x   \(\frac{1}{7}\) =  \(\frac{1}{21}\) =  \(\frac{c}{21}\)

Ta thấy:

\(\frac{a}{15}\) =  \(\frac{b}{10}\) =  \(\frac{c}{21}\) = \(\frac{a+b+c}{15+10+21}\) = \(\frac{230}{46}\)= 5

Vậy ...... ( Bạn tự làm tiếp )

~ Bài này mik làm bừa !!! Sai thì mong bn bỏ qua

~ Hok T ~

Gọi số phải tìm là ¯¯¯¯¯¯¯¯abcabc¯.Xét 

P=¯¯¯¯¯¯¯¯abca+b+c=1+99a+9ba+b+cP=abc¯a+b+c=1+99a+9ba+b+c Min ⇔c=9⇔c=9

Khi đó P=1+99a+9ba+b+9=1+9(a+b+9)+90a−81a+b+9=10+90a−81a+b+9P=1+99a+9ba+b+9=1+9(a+b+9)+90a−81a+b+9=10+90a−81a+b+9

PP min khi chỉ khi b=9b=9 và a=1a=1

Số cần tìm là 199

học tốt nha (>v<)

Đáp án :
-Gọi số có ba chữ số cần tìm là ¯¯¯¯¯abcabc¯ (a;b;c∈N;0<a≤9;0≤b;c≤9)(a;b;c∈N;0<a≤9;0≤b;c≤9)
 Ta có : k=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯abca+b+c=100a+100b+ca+b+c=1+99a+9ba+b+ck=abca+b+c¯=100a+100b+ca+b+c=1+99a+9ba+b+c
-Với a,ba,b xác định thì kk bé nhất khi cc lớn nhất :
⇒c=9⇒c=9
k=10+99a+9ba+b+9=1+9.(a+b+9)+90a−81a+b+9k=10+99a+9ba+b+9=1+9.(a+b+9)+90a-81a+b+9
=1+9+90a−81a+b+9=10+90a−81a+b+9=1+9+90a-81a+b+9=10+90a-81a+b+9
Với aa xác định thì kk bé nhất khi bb lớn nhất :
⇒b=9⇒b=9
k=10+90a−81a+18=10+9.10a−9a+18=10+9.10(a+18)−189a+18k=10+90a-81a+18=10+9.10a-9a+18=10+9.10(a+18)-189a+18
=10+90−9.189a+18=190−9.189a+18=10+90-9.189a+18=190-9.189a+18 bé nhất khi aa bé nhất
⇒a=1⇒a=1
Vậy số phải tìm là 199199 và k=19919k=19919

Sai thôi bn nhé