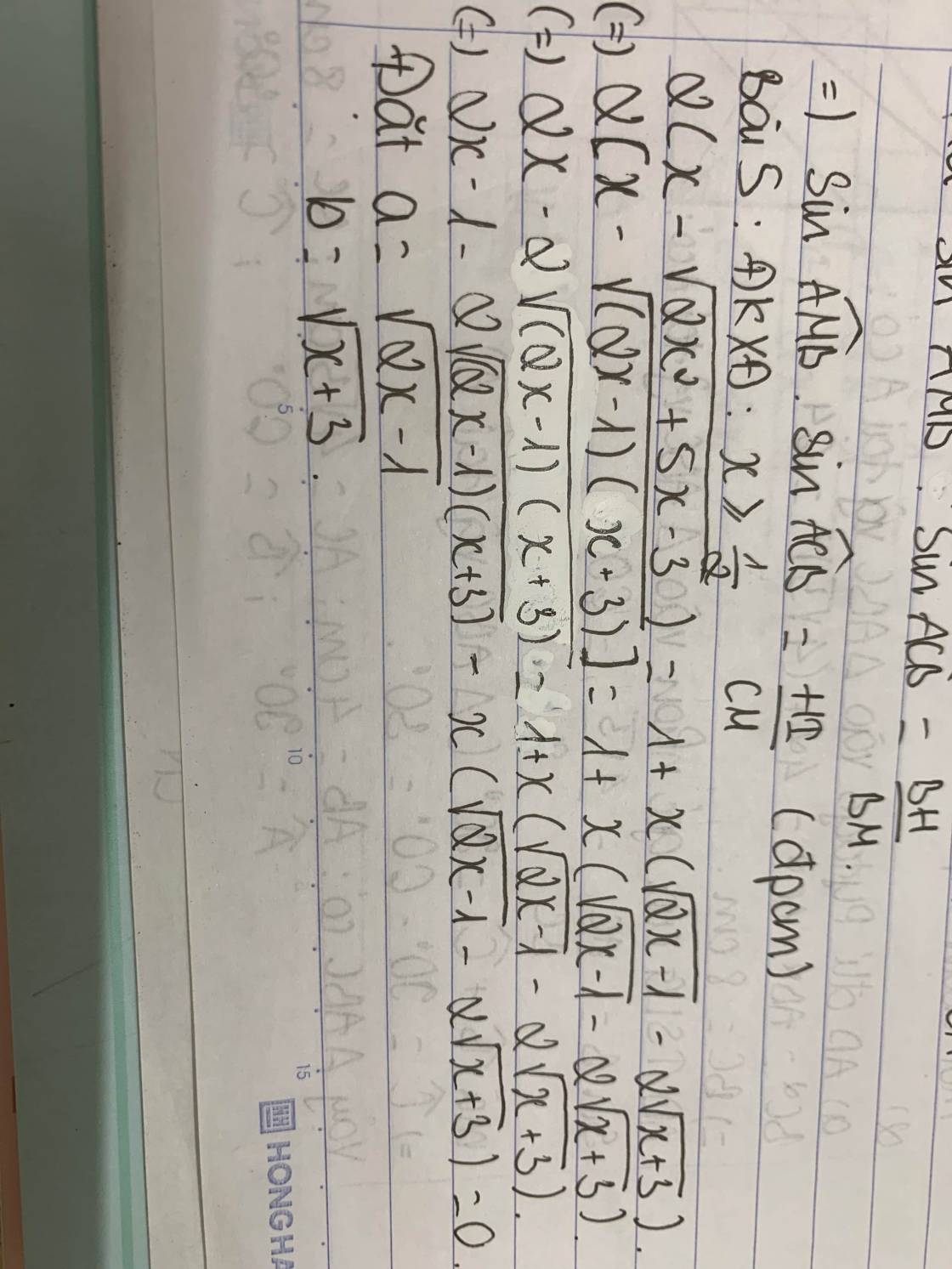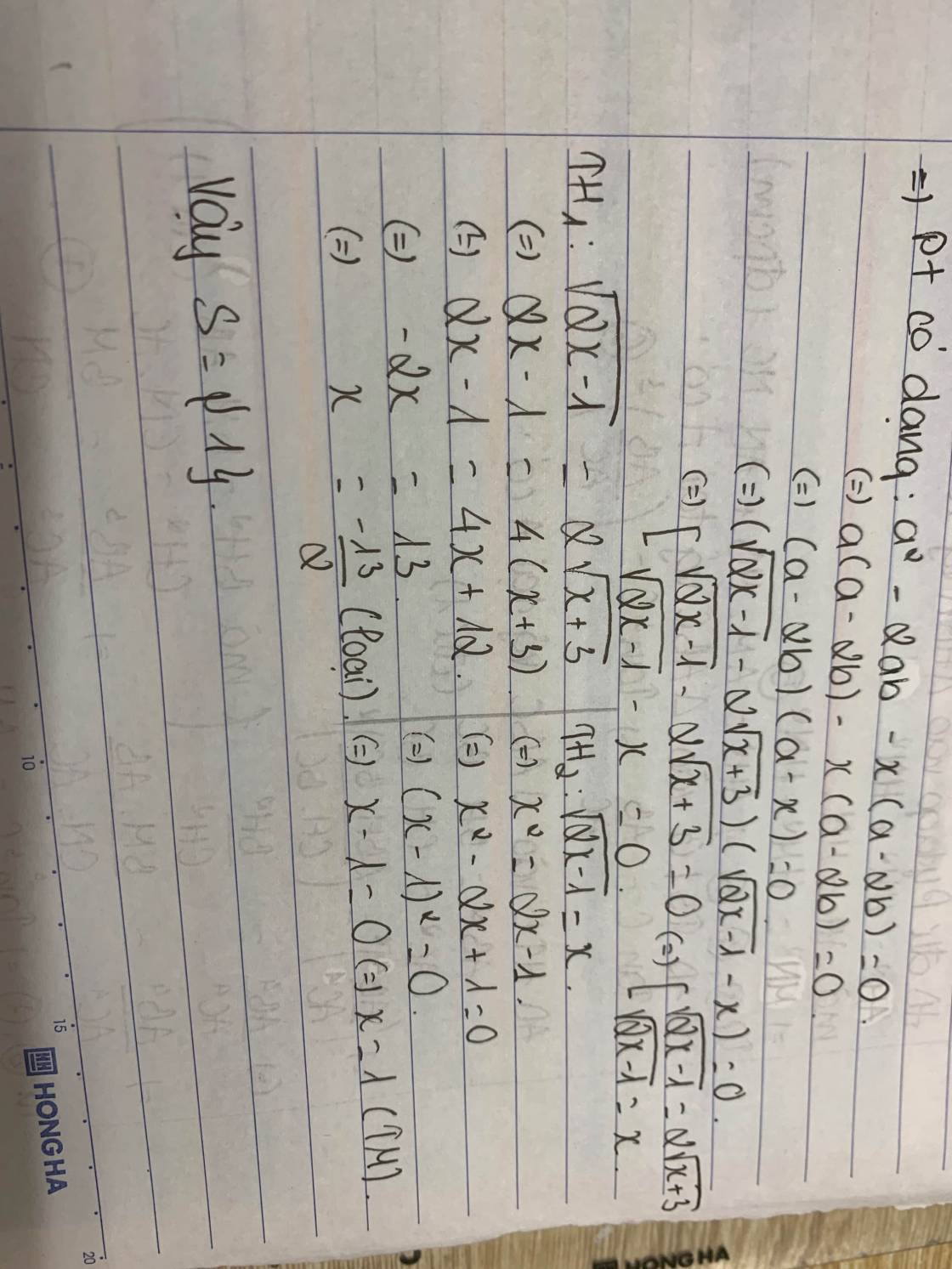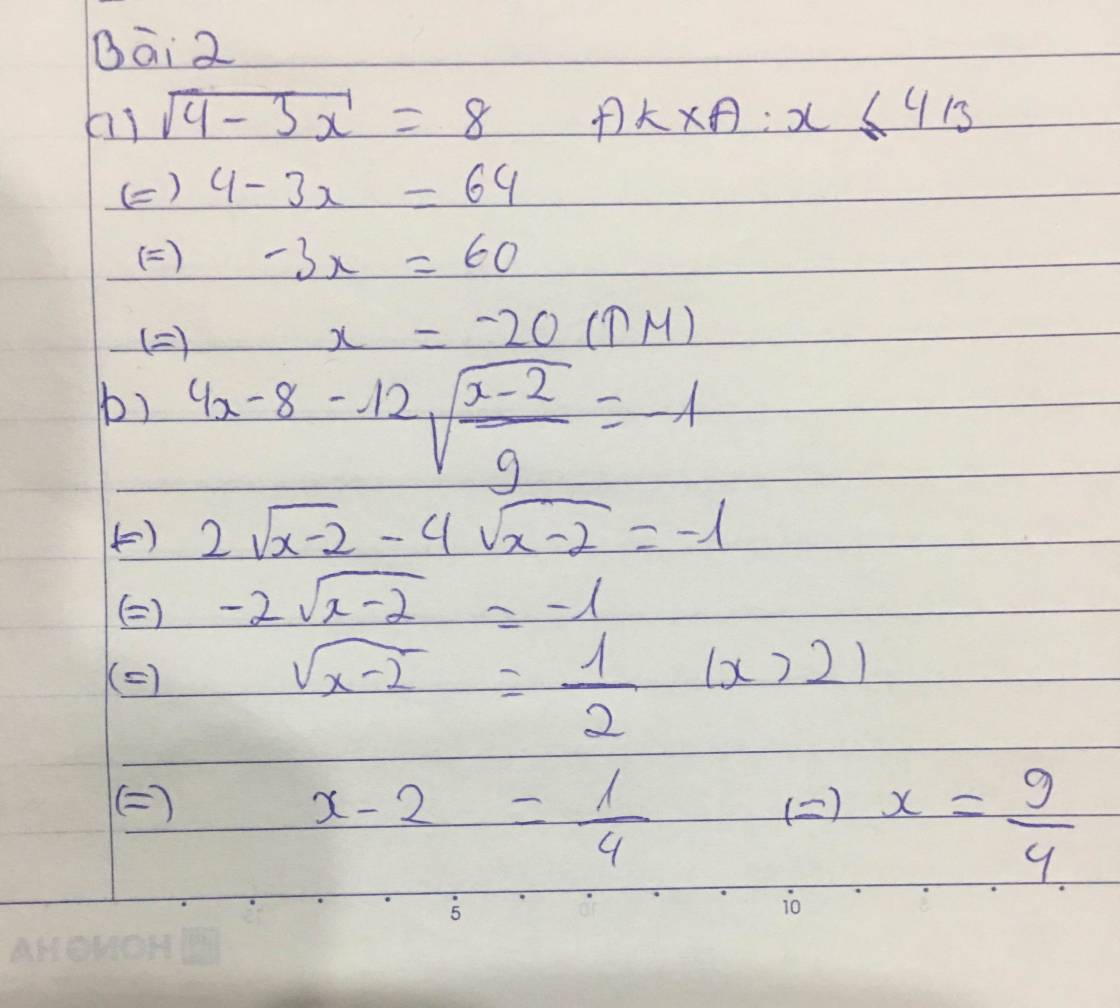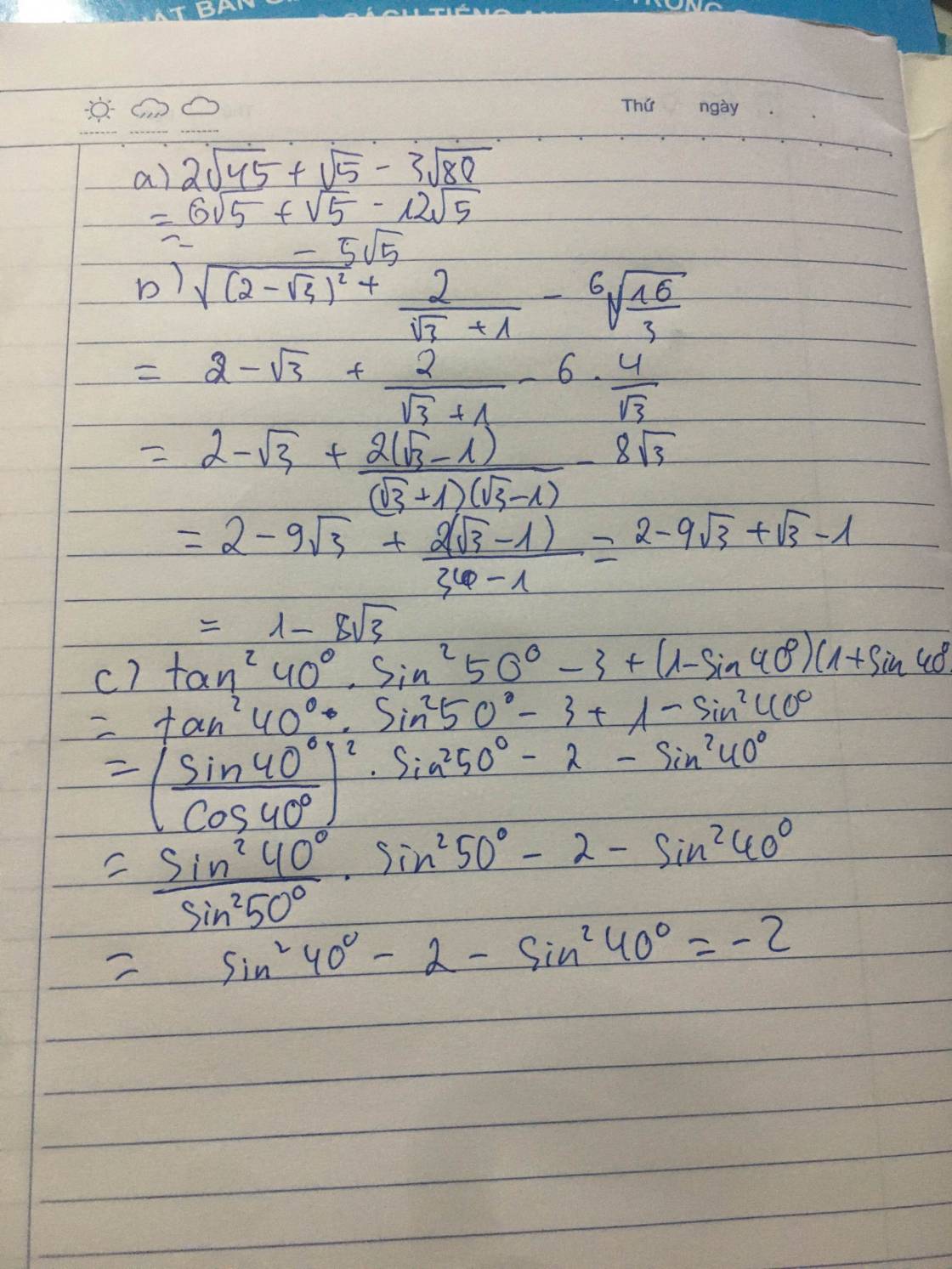cho (O) đường kính ab dây cd (c,d thuộc nửa mặt phẳng bờ ab) gọi h,k theo thứ tự chân đường vuông góc kẻ từ a,b đến cd gọi i là trung điểm cd cmr OH=OK gọi e là giao điểm của bk với (o) chứng minh OI vuông góc với AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải phương trình:
$$ 2\left(x-\sqrt{2 x^2+5 x-3}\right)=1+x(\sqrt{2 x-1}-2 \sqrt{x+3}) \text {. }$$

ĐKXĐ : \(\left\{{}\begin{matrix}2x^2+5x-3\ge0\\2x-1\ge0\\x+3\ge0\end{matrix}\right.\)
Phương trình tương đương : \(2x-2\sqrt{2x^2+5x+3}=1+x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow2x-1-2\sqrt{\left(2x-1\right)\left(x+3\right)}=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\sqrt{2x-1}.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\left(\sqrt{2x-1}-x\right).\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x-1}=x\\\sqrt{2x-1}=2\sqrt{x+3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{13}{2}\left(\text{loại}\right)\end{matrix}\right.\)
Vậy x = 1 là nghiệm phương trình

b ) ĐKXĐ : x ≥ 2
\(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=-1\)
\(\sqrt{4.\left(x-2\right)}-\dfrac{12}{3}\sqrt{x-2}=-1\)
\(2\sqrt{x-2}-4\sqrt{x-2}=-1\)
\(-2\sqrt{x-2}=-1\)
\(\sqrt{x-2}=\dfrac{1}{2}\)
\(\left(\sqrt{x-2}\right)^2=\left(\dfrac{1}{2}\right)^2\)
\(x-2=\dfrac{1}{4}\)
\(x=\dfrac{1}{8}\)
Vậy biểu thức vô nghiệm
a ) \(\sqrt{4-3x}=8\)
\(\left(\sqrt{4-3x}\right)^2=8^2\)
\(4-3x=8\)
\(-3x=4\)
\(x=-\dfrac{4}{3}\)

a ) \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
= \(2\sqrt{9.5}+\sqrt{5}-3\sqrt{16.5}\) \
= \(2.3\sqrt{5}+\sqrt{5}-3.4\sqrt{5}\)
= \(6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
= \(\left(6+1-12\right)\sqrt{5}\)
= \(-5\sqrt{5}\)
b ) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
= / \(2-\sqrt{3}\) / \(+\dfrac{2.\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right).\left(\sqrt{3}-1\right)}-6\sqrt{\dfrac{48}{3^2}}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{\sqrt{3}^2-1^2}-\dfrac{6}{3}\sqrt{48}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{3-1}-2\sqrt{48}\)
=\(2-\sqrt{3}+\sqrt{3}-1-2\sqrt{16.3}\)
= \(2-\sqrt{3}+\sqrt{3}-1-8\sqrt{3}\)
= \(1-8\sqrt{3}\)
ý c ) em không biết làm ☹

Đề sai. Cho $a=2; b=1$ đều không chia hết cho $5$
$a^5-b^5=2^5-1=31$ không chia hết cho $5$

Lời giải:
ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow (x-2\sqrt{x}+1)+\sqrt{x-1}=0$
$\Leftrightarrow (\sqrt{x}-1)^2+\sqrt{x-1}=0$
Ta thấy: $(\sqrt{x}-1)^2\geq 0; \sqrt{x-1}\geq 0$ với mọi $x\geq 1$
Do đó để tồng trên bằng $0$ thì:
$(\sqrt{x}-1)^2=\sqrt{x-1}=0$
$\Leftrightarrow x=1$ (thỏa mãn).