Cho ABC cân tại ABC cân tại A, có H là trung điểm của cạnh BC. Vẽ HI vuông gócvới AC(H thuộccạnh AC),gọi Olàtrungđiểmcủa HI.Chứngminha) CHA∽CIH từđósuyra CH/CI=HA/IHb) BIC∽AOH .c) AOBI.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài quãng đường AB là x(km)
(ĐK: x>0)
Thời gian ô tô thứ nhất đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)
Vận tốc của ô tô thứ hai là 40+15=55(km/h)
Thời gian ô tô thứ hai đi từ A đến B là \(\dfrac{x}{55}\left(giờ\right)\)
Ô tô thứ nhất đến trước 1h30p=1,5h nên ta có:
\(\dfrac{x}{40}-\dfrac{x}{55}=1,5\)
=>\(\dfrac{11x-8x}{440}=1,5\)
=>3x=440*1,5=660
=>x=220(nhận)
Vậy: Độ dài quãng đường AB là 220km

a) Vì tam giác ABC cân tại A nên ta có:
Góc BAC = Góc BCA = 47o
Góc ABC = 180o - 2 x 47o = 86o
b) Ta có:
AB = AC (do tam giác ABC cân tại A)
BM = MC (do M là trung điểm của BC)
∠ABM = ∠ACM = 90o - 47o = 43o (do ∠BAC = 47o và ∠BAM, ∠CAM là góc vuông)
Vậy, 𝛥𝐴𝐵𝑀 = 𝛥𝐴𝐶𝑀 (theo định lý tam giác cân)
c) Ta có:
AM + BM = AB + BM (do AB = AM)
AB + BM > AC (do tổng độ dài hai cạnh của một tam giác luôn lớn hơn cạnh còn lại)
Vậy, AM + BM > AC

a:
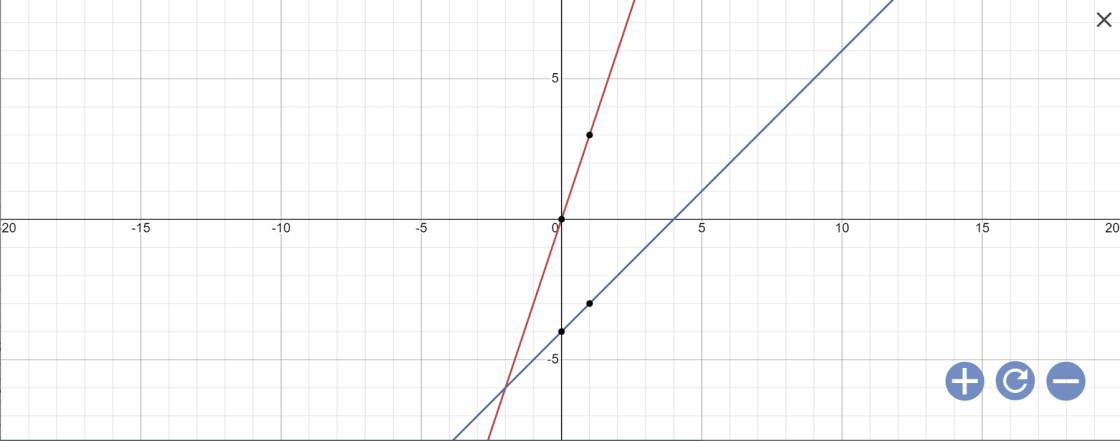
b: Phương trình hoành độ giao điểm là:
3x=x-4
=>2x=-4
=>x=-2
Thay x=-2 vào y=x-4, ta được:
y=-2-4=-6
Vậy: Tọa độ giao điểm là A(-2;-6)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>DA=DE
Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}=90^0\)
=>DE\(\perp\)BC tại E
Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó; ΔDAK=ΔDEC
=>AK=EC
c: Ta có; ΔDAK=ΔDEC
=>DK=DC
=>D nằm trên đường trung trực của KC(1)
Ta có: IK=IC
=>I nằm trên đường trung trực của KC(2)
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Từ (1),(2),(3) suy ra B,D,I thẳng hàng
A) Chứng minh Tam giác BAD = Tam giác BED
Xét hai tam giác BAD và BED, ta có:
BA = BE (theo giả thiết)
∠BAD = ∠BED (do DE là tia phân giác của ∠B)
Do đó, tam giác BAD = tam giác BED (theo trường hợp cạnh - góc - cạnh).
B) Chứng minh AK = EC
Do tam giác BAD = tam giác BED, ta có AD = ED.
Gọi K là giao điểm của BA và DE, ta có:
AK + KD = AD
EK + KD = ED
Do AD = ED, suy ra AK + KD = EK + KD. Do đó, AK = EK.
C) Chứng minh ba điểm B, D, I thẳng hàng
Gọi I là trung điểm của CK. Do AK = EK và AI = IC (do I là trung điểm), ta có tam giác AKE = tam giác ICE (theo trường hợp cạnh - cạnh - cạnh).
Do đó, ∠AKE = ∠ICE. Khi đó, ta có ∠BKI = ∠BID. Do đó, B, D, I thẳng hàng.

Tính giá trị biểu thức A = ( 121 x 46 - 242 x 23 ) x ( 1 x 1 + 2 x 2 + 3 x 3 + ... + 100 x 100 ) giúp tui với
Thời gian dự kiến sẽ đi hết quãng đường cảu người đó là:
\(\dfrac{30\times1-25\times2}{-5}=\dfrac{30-50}{-5}=\dfrac{-20}{-5}=4\left(giờ\right)\)
Độ dài quãng đường AB là:
\(25\times\left(4+2\right)=150\left(km\right)\)
Để đến sớm hơn 1 giờ thì cần đi với vận tốc là:
150:(4-1)=50(km/h)

Giải:
Chuvi của hình chữ nhật là chu vi của hình vuông và bằng:
(11 + 5) x 2 = 32 (cm)
Cạnh hình vuông là: 32 : 4 = 8 (Cm)
Diện tích của tờ giấy hình vuông là: 8 x 8 = 64 (cm2)
Chọn a; và c

Số sinh viên trường Đại học B ít hơn trường Đại học A sau khi tuyển sinh viên mới là:
21414 + 7245 - 5419 = 19240 (sinh viên)
Đáp số: 19240 sinh viên.

Ta có: AK+KB=AB
AH+HC=AC
mà AK=AH và AB=AC
nên KB=HC
Xét ΔKBC và ΔHCB có
KB=HC
\(\widehat{KBC}=\widehat{HCB}\)
CB chung
Do đó: ΔKBC=ΔHCB
=>\(\widehat{KCB}=\widehat{HBC}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
=>OB=OC
=>O nằm trên đường trung trực của BC
Bạn nên ghi hẳn đề bài ra để mọi người hỗ trợ tốt hơn nhé.
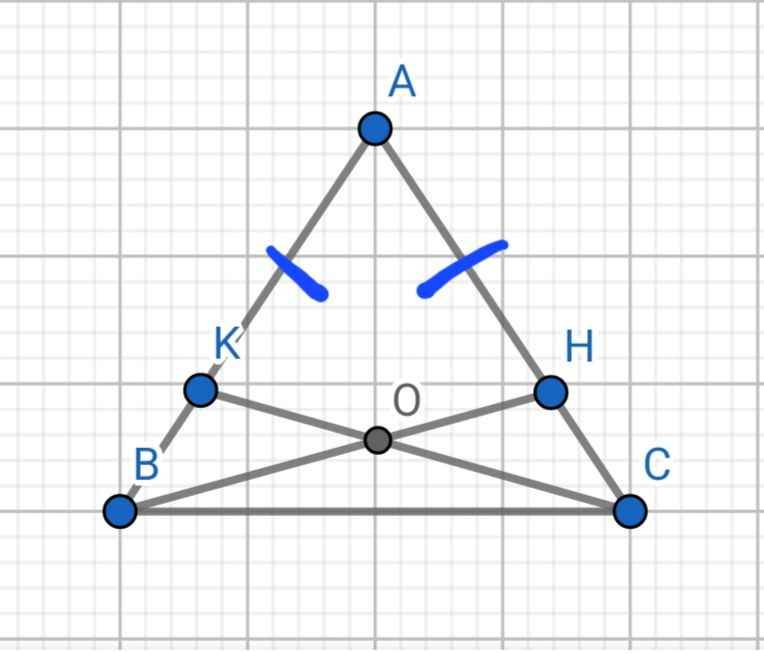 Chứng minh điểm O thuộc trung trực của đoạn thẳng BC
Chứng minh điểm O thuộc trung trực của đoạn thẳng BC
a: Xét ΔCHA vuông tại H và ΔCIH vuông tại I có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCIH
=>\(\dfrac{CH}{CI}=\dfrac{HA}{IH}\)
b:
Ta có; ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Ta có: \(\dfrac{CH}{CI}=\dfrac{HA}{IH}\)
=>\(CI\cdot HA=CH\cdot IH=\dfrac{1}{2}\cdot BC\cdot2\cdot OH=BC\cdot OH\)
=>\(\dfrac{CI}{OH}=\dfrac{BC}{HA}\)
Xét ΔBIC và ΔAOH có
\(\dfrac{BC}{AH}=\dfrac{CI}{OH}\)
\(\widehat{BCI}=\widehat{AHO}\left(=90^0-\widehat{HAI}\right)\)
Do đó ΔBIC~ΔAOH