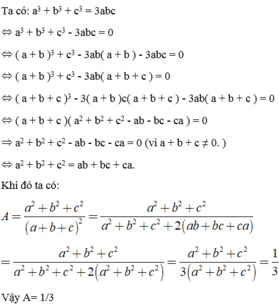Tìm các số nguyên x,y thoả mãn: x^4 +2x^3 +x^2 + x+ 3= y^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$(xy)^2-xy-2=(x^2y^2+xy)-(2xy+2)$
$=xy(xy+1)-2(xy+1)=(xy+1)(xy-2)$
b. Bạn xem lại đoạn $-16x^2$ là dấu - hay + vậy?

\(4x^2+8x=0\)
\(\Leftrightarrow4x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
a) \(4x^2+8x=0\)
\(\Rightarrow4x\left(x+8\right)=0\)
\(\Rightarrow4x=0\) hoặc \(x+8=0\)
\(TH1:4x=0\Rightarrow x=4:0\Rightarrow x=0\)
\(TH2:x+8=0\Rightarrow x=0-8\Rightarrow x=-8\)
Vậy nghiệm của đa thức \(4x^2+8x=0\) là: \(\left\{0;-8\right\}\)

Thay đa thức \(b=2xy+y+3\) (1) tại \(x=1;y=2\) vào đa thức (1) ta có:
\(\Rightarrow b=2.1.2+2+3\)
\(\Rightarrow b=4+2+3\)
\(\Rightarrow b=9\)
Vậy giá trị của đa thức (1) tại \(x=1;y=2\) là: \(9\)

Ta có
\(\left(a+b\right)^2=a^2+b^2+2ab=1\Rightarrow a^2+b^2=1-2ab\) (1)
Ta có
\(\left(a+b\right)^4=\left(a^2+b^2+2ab\right)^2=\)
\(=a^4+b^4+4a^2b^2+2a^2b^2+4ab^3+4a^3b=\)
\(=a^4+b^4+6a^2b^2+4ab\left(a^2+b^2\right)=1\)
\(\Rightarrow a^4+b^4=1-6a^2b^2-4ab\left(1-2ab\right)=\)
\(=1-6a^2b^2-4ab+8a^2b^2=\)
\(=1+2a^2b^2-4ab\) (2)
Ta có
\(a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=\)
\(=1-2ab-ab=1-3ab=1\Rightarrow ab=0\)
Thay \(ab=0\) vào (1) và (2)
\(a^2+b^2=1-2ab=1\)
\(a^4+b^4=1+2a^2b^2-4ab=1\)
\(\Rightarrow a^2+b^2=a^4+b^4\)

1/
\(x^2+y^2=\left(x-y\right)^2+2xy=2^2+2.1=6\)
2/
\(x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)=2\left(6+1\right)=14\)
3/
\(x^2-y^2=\left(x-y\right)\left(x+y\right)=2\left(x+y\right)\) (3)
Ta có
\(x^2+y^2=\left(x+y\right)^2-2xy=\left(x+y\right)^2-2=6\)
\(\Rightarrow\left(x+y\right)^2=8\Rightarrow\left(x+y\right)=\pm2\sqrt{2}\) Thay vào (3)
\(\Rightarrow x^2-y^2=2.\pm2\sqrt{2}=\pm4\sqrt{2}\)
4/
\(x^6-y^6=\left(x^3-y^3\right)\left(x^3+y^3\right)\) (4)
Ta có
\(x^3-y^3=14\) (cmt)
Ta có
\(x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)=\left(x+y\right).5=\pm2\sqrt{2}.5=\pm10\sqrt{2}\)
\(\Rightarrow x^6-y^6=\pm10\sqrt{2}.14=\pm140\sqrt{2}\)

Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)