Cho tam giác ABC cân tại A, các điểm D, E lần lượt thuộc các cạnh AB, AC sao cho AD=CE. Từ E kẻ tia EK song song với AB ( K thuộc BC). Gọi M là giao điểm của AK và DE.
a) Chứng minh rằng: M là trung điểm của AK và DE.
b) Vẽ đường tròn tâm M bán kính MK, đường tròn này cắt BC tại điểm thứ hai là H( H không trùng với K). Chứng minh rằng H là trung điểm của BC.



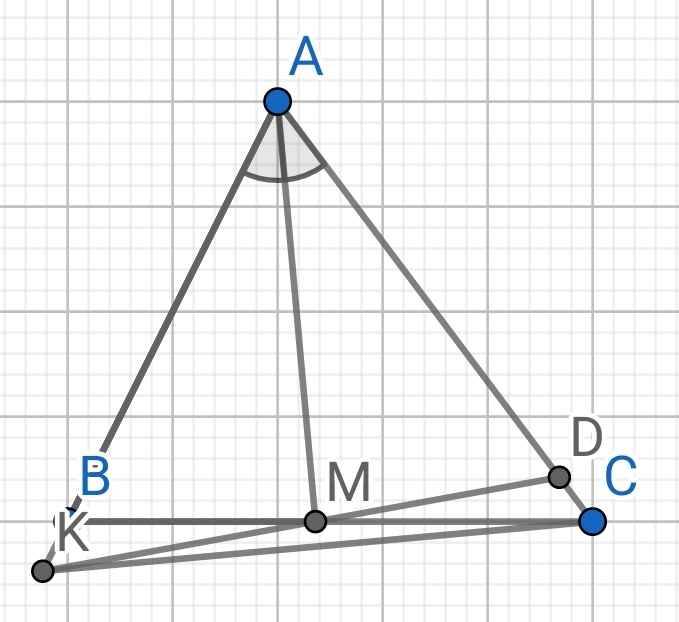
A B C E K H D M
a/
Ta có
\(\widehat{B}=\widehat{C}\) (góc ở đáy tg cân ABC)
EK//AB \(\Rightarrow\widehat{EKC}=\widehat{B}\) (góc đồng vị)
\(\Rightarrow\widehat{EKC}=\widehat{C}\) => tg EKC cân tại E => CE=EK
Mà AD=CE
=> AD=EK (1)
Ta có
EK//AB => EK//AD (2)
Từ (1) và (2) => ADKE là hình bình hành (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
=> MA=MK; MD=ME (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
b/
Ta có \(H\in\left(M;MK\right)\) => MH=MK
Mà MK=MA (cmt)
=> MH=MK=MA
=> tg MHK cân tại M \(\Rightarrow\widehat{MHK}=\widehat{MKH}\)
\(\widehat{HMK}+\widehat{MHK}+\widehat{MKH}=\widehat{HMK}+2\widehat{MHK}=180^o\) (tổng các góc trong của 1 tg = 180 độ)
MH=MK=MA (cmt) => tg MAH cân tại M
\(\Rightarrow\widehat{MAH}=\widehat{MHA}\)
\(\widehat{HMK}=\widehat{MAH}+\widehat{MHA}\) (trong tg góc ngoài bằng tổng 2 góc trong không kề với nó)
\(\Rightarrow\widehat{HMK}=2\widehat{MHA}\)
Từ \(\widehat{HMK}+2\widehat{MHK}=180^o\Rightarrow2\widehat{MHA}+2\widehat{MHK}=180^o\)
\(\Rightarrow\widehat{MHA}+\widehat{MHK}=\widehat{AHK}=90^o\Rightarrow AH\perp BC\)
Xét tg vuông ABH và tg vuông ACH có
AH chung
AB=AC (cạnh bên tg cân ABC)
=> tg AHB = tg AHC (Hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)
=> HB=HC
Em cảm ơn ạ