Trong các số tự nhiên từ 1 đến 2019 có bao nhiêu số không chia hết cho 5?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(-12\right).8\) với \(\left(-19\right).3\)
Ta có:
\(\left(-12\right).8=\left(-96\right)\)
\(\left(-19\right).3=\left(-57\right)\)
Mà \(\left(-96\right)< \left(-57\right)\) nên \(\left(-12\right).8< \left(-19\right).3\)

999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
A = 9 + 99 + 999 + ... + 999..99 (2019 chữ số 9)
Tổng tất cả các chữ số của A là:
B = 9 + 9 x 2 + 9 x 3 + 9 x 2019
B = 9 x (1 + 2 + 3+ ... + 2019)
B = 9 x (2019 + 1)x[(2019 - 1) : 1 + 1] : 2
B = 18352710

Lời giải:
$T = \frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+....+\frac{99}{7^{100}}$
$7T = \frac{1}{7}+\frac{2}{7^2}+\frac{3}{7^3}+....+\frac{99}{7^{99}}$
$\Rightarrow 6T=7T-T = \frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+...+\frac{1}{7^{99}}-\frac{99}{7^{100}}$
$42T = 1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{98}}-\frac{99}{7^{99}}$
$\Rightarrow 42T-6T = 1-\frac{100}{7^{99}}+\frac{99}{7^{100}}$
$\Rightarrow 36T = 1-\frac{601}{7^{100}}< 1$
$\Rightarrow T< \frac{1}{36}$


\(a,-\dfrac{9}{4}< 0;\dfrac{1}{3}>0.Nên:-\dfrac{9}{4}< \dfrac{1}{3}\\ b,-\dfrac{8}{3}< -2;\dfrac{4}{-7}>-1.Nên:-\dfrac{8}{3}< -2< -1< \dfrac{4}{-7}\\ Vậy:-\dfrac{8}{3}< \dfrac{4}{-7}\\ c,\dfrac{9}{-5}< -1;\dfrac{7}{-10}>-1.Nên:\dfrac{9}{-5}< -1< \dfrac{7}{-10}.Vậy:\dfrac{9}{-5}< \dfrac{7}{-10}\\ d,\dfrac{3}{14}>0;-\dfrac{6}{14}< 0.Nên:\dfrac{3}{14}>0>-\dfrac{6}{14}.Vậy:\dfrac{3}{14}>-\dfrac{6}{14}\\ e,\dfrac{7}{-12}=\dfrac{7.3}{-12.3}=\dfrac{21}{-36};\dfrac{11}{-18}=\dfrac{11.2}{-18.2}=\dfrac{22}{-36}\\ Vì:\dfrac{21}{-36}>\dfrac{22}{-36}.Nên:\dfrac{7}{-12}>\dfrac{11}{-18}\)
\(f,-\dfrac{4}{7}< -\dfrac{1}{2};-\dfrac{4}{10}>\dfrac{-1}{2}.Nên:-\dfrac{4}{7}< -\dfrac{1}{2}< -\dfrac{4}{10}.Vậy:-\dfrac{4}{7}< -\dfrac{4}{10}\\ g,-\dfrac{8}{15}< -\dfrac{1}{2};\dfrac{5}{-24}>-\dfrac{1}{2}.Nên:-\dfrac{8}{15}< -\dfrac{1}{2}< \dfrac{5}{-24}.Vậy:-\dfrac{8}{15}< \dfrac{5}{-24}\\ h,\dfrac{69}{-230}=\dfrac{69:23}{-230:23}=\dfrac{3}{-10};\dfrac{-39}{143}=\dfrac{-39:13}{143:13}=\dfrac{-3}{11}\\ Vì:\dfrac{-3}{10}< -\dfrac{3}{11}.Vậy:\dfrac{69}{-230}< \dfrac{-39}{143}\\ i,\dfrac{7}{41}=1-\dfrac{34}{41};\dfrac{13}{47}=1-\dfrac{34}{47}\\ Vì:\dfrac{34}{41}>\dfrac{34}{47}.Nên:1-\dfrac{34}{41}< 1-\dfrac{34}{47}.Vậy:\dfrac{7}{41}< \dfrac{13}{47}\)

suy ra: 20 x 21 = 12 x ( 41- x)
420 = 492 -12x
12x= 492-420
12x= 72
x= 72 ;12
x = 6
vậy x=6

25 x 4 + 25 x 7 + 25
= 25 x 4 + 25 x 7 + 25 x 1
= 25 x (4 + 7 + 1)
= 25 x 12
= 300

Tổng số tuổi 2 chị em Quyên:
40 : 2 = 20 (tuổi)
Khi mẹ 49 tuổi thì hai chị em Quyên tổng tuổi là:
(49 - 40) x 2 + 20 = 38 (tuổi)
Khi mẹ 49 tuổi thì Quyên:
(38 - 6):2= 16 (tuổi)
Khi mẹ 49 tuổi thì chị của Quyên:
16 + 6 = 22 (tuổi)
Đ.số::............
 Trả lời lẹ giúp em đi ạ
Trả lời lẹ giúp em đi ạ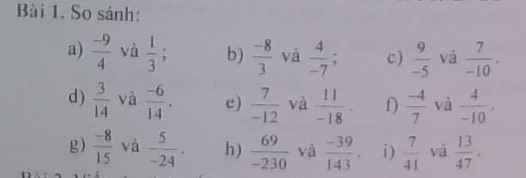
Số lượng số tự nhiên chia hết cho 5 từ 1 đến 2019:
(2015 - 5):5 + 1 = 403 (số)
Số lượng số tự nhiên không chia hết cho 5 từ 1 đến 2019:
(2019 - 1 + 1) - 403 = 1616 (số)
Đ.số:......
Dãy số các số chia hết cho 5 từ 1 đến 2019 là:
5; 10; 15 ; 20; 25; ... ; 2015.
Số số hạng các số chia hết cho 5 từ 1 đến 2019 là:
\(\left(2015-5\right):5+1=403\left(số\right)\)
Số số hạng các số tự nhiên không chia hết cho 5 từ 1 đến 2019 là:
\(\left(2019-1+1\right)-403=1616\left(số\right)\)
Đáp số: \(1616\) số.