Cho tam giác nhọn ABC có AD là phân giác trong góc A (D thuộc BC). Đường thẳng qua D song song với AB cắt AC tại I, đường thẳng qua D song song với AC cắt AB tại K. Chứng minh rằng tam giác IDK là tam giác cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
1
16 tháng 2 2021
Ta có: 2020(x-2019)^2 >=0
=> 25-y^2 >=0 (1)
Lại có 2020(x-2019)^2 chia hết cho 2020 => 25-y^2 chia hết cho 2020 (2)
Mặt khác y^2>=0 =>25-y^2<=25 (3)
Từ(1),(2),(3) =>25-y^2=0 <=> y= 5 hoặc -5
Khi này : 2020(x-2019)^2=0 <=> x=2019
Vậy x=2019;y = 5 hoặc -5
NH
1
17 tháng 2 2021
xy+4x=35+5y
xy+4x-5y-20=15
x(y+4)-5(y+4)=15
(y+4)(x-5)=15
Mà x,y nguyên (bạn thiếu đk này) => y+4 ,x-5 nguyên
Ta có bảng sau:
| y+4 | 1 | 3 | 5 | 15 | -1 | -3 | -5 | -15 |
| x-5 | 15 | 5 | 3 | 1 | -15 | -5 | -3 | -1 |
| y | -3 | -1 | 1 | 11 | -5 | -7 | -9 | -19 |
| x | 20 | 10 | 8 | 6 | -10 | 0 | 2 | 4 |
Ta kết luận có 8 cặp giá trị x,y thỏa mãn.
17 tháng 2 2021
2xy^2-10x+y^2=17
(2xy^2+y^2) - (10x+5)=12
y^2(2x+1)-5(2x+1)=12
(2x+1)(y^2-5)=12
Mà x,y nguyên => 2x+1 là số lẻ; y^2-5 là số nguyên
Ta có bảng sau:
| 2x-1 | 1 | 3 | -1 | -3 |
| y^2-5 | 12 | 4 | -12 | -4 |
| x | 1 | 2 | 0 | -1 |
| y | không nguyên | 3 hoặc -3 | không tồn tại | 1 hoặc -1 |
Kết luận : tồn tại 4 cặp giá trị x,y thỏa mãn
HK
1
17 tháng 2 2021
Ta có: \(7^{45}-3^{35}=7.7^{44}-3^3.3^{32}=7.\left(7^4\right)^{11}-27.\left(3^4\right)^8=7.\left(\overline{...1}\right)^{11}-27.81^8\)\(7.\left(\overline{...1}\right)-27.\left(\overline{...1}\right)=\overline{...7}-\overline{...7}=\overline{...0}\)
Vì \(7^{45}-3^{35}\) có chữ số tận cùng là \(0\) chia hết cho \(10\)
nên \(7^{45}-3^{35}⋮10\) (đpcm)
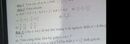
Xét tứ giác \(AIDK\):
\(AI//DK,AK//DI\)
Suy ra \(AIDK\)là hình bình hành.
mà \(AD\)là phân giác trong của góc \(\widehat{IAK}\)nên \(AIDK\)là hình thoi .
Suy ra \(DK=DI\)
do đó tam giác \(IDK\)là tam giác cân.