205: \(f\left(x\right)=x^2-x+1\)

\(=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)

=>f(x) không có nghiệm thực

204:

a: \(f\left(-1\right)=\left(-1\right)^4+5\cdot\left(-1\right)^3+3\cdot\left(-1\right)^2+2\cdot\left(-1\right)+3\)

\(=1-5+3-2+3\)

=7-7=0

=>x=-1 là nghiệm của f(x)

\(g\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3+\left(-1\right)^2-7\cdot\left(-1\right)-10\)

\(=3-1+1+7-10=10-10=0\)

=>x=-1 là nghiệm của g(x)

\(h\left(-1\right)=4\cdot\left(-1\right)^3+2\cdot\left(-1\right)^2-\left(-1\right)+1\)

\(=-4+2+1+1=0\)

=>x=-1 là nghiệm của h(x)

khoảng 40-45

40-45 kg

Cho:

Điền hệ số thích hợp vào ô trống.
$P(x)+Q(x)=$ $($�3x3$)$ $+$ $($�2x2$)$$+$ $($$x$$)$ $+$ $($$)$

P(x)+Q(x)

\(=3x^2-3x+6+4x^3-5x^2+x-3\)

\(=4x^3-2x^2-2x+3\)

a: Xét ΔAHB và ΔAHC có

AH chung

HB=HC

AB=AC

Do đó: ΔAHB=ΔAHC

b: Ta có: ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

mà \(\widehat{BAH}=\widehat{CKA}\)(hai góc so le trong, BA//CK)

nên \(\widehat{CAK}=\widehat{CKA}\)

=>ΔCAK cân tại C

=>CA=CK

mà CA=BA

nên CK=BA

Ta có: ΔAHB=ΔAHC

=>\(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

=>AH\(\perp\)BC

Ta có: ΔCAK cân tại C

mà CH là đường cao

nên H là trung điểm của AK

Xét ΔBAK có

BH là đường cao

BH là đường trung tuyến

Do đó: ΔBAK cân tại B

=>BA=BK

c: Đề sai rồi bạn

a: Xét ΔABD và ΔACD có

AB=AC

\(\widehat{BAD}=\widehat{CAD}\)

AD chung

Do đó: ΔABD=ΔACD

=>\(\widehat{ADB}=\widehat{ADC}\)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

=>AD\(\perp\)BC

ta có: ΔABD=ΔACD

=>BD=CD

=>D là trung điểm của BC

mà AD\(\perp\)BC tại D

nên AD là đường trung trực của BC

b: 

Cách 1:

XétΔEDB vuông tại D và ΔEDC vuông tại E có

ED chung

DB=DC

Do đó: ΔEDB=ΔEDC

=>EB=EC

=>ΔEBC cân tại E

Cách 2:

Xét ΔEBC có

ED là đường cao

ED là đường trung tuyến

Do đó: ΔEBC cân tại E

a: \(M\left(x\right)=N\left(x\right)+E\left(x\right)\)

=>N(x)=M(x)-E(x)

\(=3x^2+4x+1-x^3+3x^2+3x+1=-x^3+6x^2+7x+2\)

b: \(M\left(1\right)=3\cdot1^2+4\cdot1+1=8\)>0

=>x=1 không là nghiệm của M(x)

Ta có: \(x:2=y:3\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{y-x}{3-2}=\dfrac{1}{1}=1\)

Do đó:

\(\dfrac{x}{2}=1=>x=2.1=2\)

\(\dfrac{y}{3}=1=>y=3.1=3\)

Vậy x = 2; y = 3.

`#NqHahh`

Sửa bài:

Ta có: \(x:2=y:3=>\dfrac{x}{2}=\dfrac{y}{3}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=>\dfrac{y-x}{3-2}=\dfrac{-1}{1}=-1\)

Do đó:

\(\dfrac{x}{2}=-1=>x=2.\left(-1\right)=-2\)

\(\dfrac{y}{3}=-1=>y=3.\left(-1\right)=-3\)

Vậy x = -2; y = -3.

`#NqHahh`

5: M nằm trên đường trung trực của EF

=>ME=MF

N nằm trên đường trung trực của EF

=>NE=NF

Xét ΔMEN và ΔMFN có

ME=MF

NE=NF

MN chung

Do đó; ΔMEN=ΔMFN

Bài 4:

AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: DB=DC

=>D nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra AD là đường trung trực của BC

=>AD\(\perp\)BC tại trung điểm của BC

=>M là trung điểm của BC

Bài 5

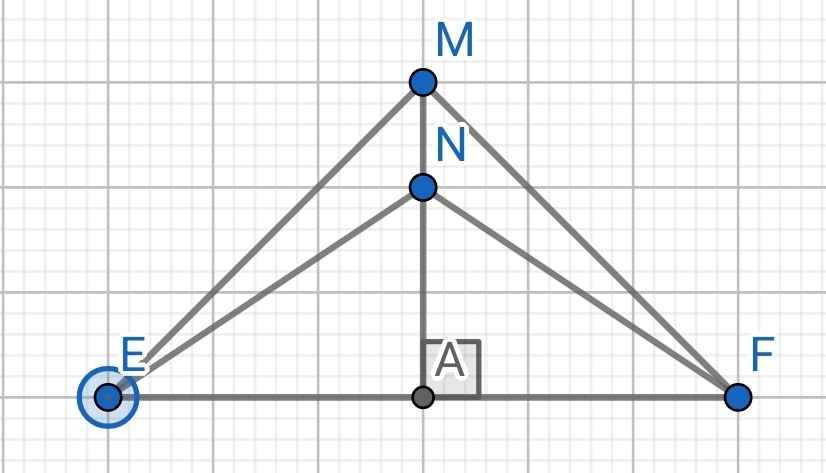
Do M nằm trên đường trung trực của EF (gt)

⇒ ME = MF

Do N nằm trên đường trung trực của EF (gt)

⇒ NE = NF

Xét ∆EMN và ∆FMN có:

MN là cạnh chung

ME = MF (cmt)

NE = NF (cmt)

⇒ ∆EMN = ∆FMN (c-c-c)

a là đường trung trực của AB

=>a\(\perp\)AB

mà B\(\in\)AC

nên a\(\perp\)AC

b là đường trung trực của BC

=>b\(\perp\)BC

mà B\(\in\)AC

nên b\(\perp\)AC

Ta có: a\(\perp\)AC

b\(\perp\)AC

Do đó: a//b

Ta có: a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC nên \(a \bot AB,b \bot BC\).

Mà ba điểm A, B, C thẳng hàng với nhau nên đường thẳng a và b không cắt nhau và chúng cùng vuông góc với đường thẳng chứa ba điểm A, B, C.

Vậy a // b. 

Phương trình bậc 2 có dạng  a+b+c=0

\(\Rightarrow x_1=1;x_2=\dfrac{c}{a}=\dfrac{13}{5}\)

Ta có:

a + b + c = 5 + (-18) + 13 = 0

Phương trình có hai nghiệm:

x₁ = 1; x₂ = 13/5