\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\) \(\Rightarrow\dfrac{2x}{4}=\dfrac{y}{3}=\dfrac{z}{4}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{2x}{4}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{4+3-4}=\dfrac{6}{3}=2\)

\(\dfrac{x}{2}=2\Rightarrow x=2.2=4\)

\(\dfrac{y}{3}=2\Rightarrow y=2.3=6\)

\(\dfrac{z}{4}=2\Rightarrow z=2.4=8\)

Vậy \(x=4;y=6;z=8\)

(n-4) chia hết (n-1)

Suy ra : (n-1)-3 chia hết (n-1)

Suy ra : -3 chia hết (n-1)

n-1       1 ; -1 ; 3 ; -3

n          2 ; 0 ; 4 ; -2

 Vậy n thuộc {2;0;4;-2)

Ta có:

\(n-4=n-1-3\)

Để \(\left(n-4\right)⋮\left(n-1\right)\) thì \(3⋮\left(n-1\right)\)

\(\Rightarrow n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

\(\Rightarrow n\in\left\{-2;0;2;4\right\}\)

805 yến

\(8tấn5yến=850yến\)

Đề thiếu, em bổ sung đề lại

hình như đề thiếu bạn ạ

mong bạn bổ sung lại đề

A = \(\dfrac{1+2+2^2+...+2^{2004}}{1+2^5+2^{10}+...+2^{2000}}\)

Đặt B =  1 + 2 + 2² + ... + 2²⁰⁰⁴

      2B = 2 + 2² + 2³ + ...+ 2²⁰⁰⁵

      2B - B = (2 + 2² + 2³ + ... + 2²⁰⁰⁵) - (1 + 2 + 2² + .. + 2²⁰⁰⁴)

       B = 2 + 2² + 2³ + ... + 2²⁰⁰⁵ - 1 - 2  - 2² - ... - 2²⁰⁰⁴

      B = (2 - 2) + (2² - 2²) + (2³ - 2³) + ... (2²⁰⁰⁴ - 2²⁰⁰⁴) + (2²⁰⁰⁵ - 1)

      B = 2²⁰⁰⁵ - 1

Đặt  C =  1  + 2⁵ + 2¹⁰ + ...   + 2²⁰⁰⁰

     2⁵C = 2⁵ + 2¹⁰ + 2¹⁵ + ... + 2²⁰⁰⁵

     32C - C = (2⁵ + 2¹⁰ + 2¹⁵ + ... + 2²⁰⁰⁵) - (1 + 2⁵ + 2¹⁰ +... +2²⁰⁰⁰)

     31C      =  2⁵ + 2¹⁰ + 2¹⁵ + ... + 2²⁰⁰⁵ - 1 - 2⁵ - 2¹⁰ - ... - 2²⁰⁰⁰

     31C      =(2⁵ - 2⁵) + (2¹⁰ - 2¹⁰) +...+ (2²⁰⁰⁰ - 2²⁰⁰⁰) + (2²⁰⁰⁵ - 1)

     31C     = 2²⁰⁰⁵ - 1

         C = \(\dfrac{2^{2005}-1}{31}\)

A = \(\dfrac{B}{C}\) = \(\dfrac{2^{2005}-1}{\dfrac{2^{2005}-1}{31}}\)

A = ( \(2^{2005}-1\)) x \(\dfrac{31}{2^{2005}-1}\)

A = 31

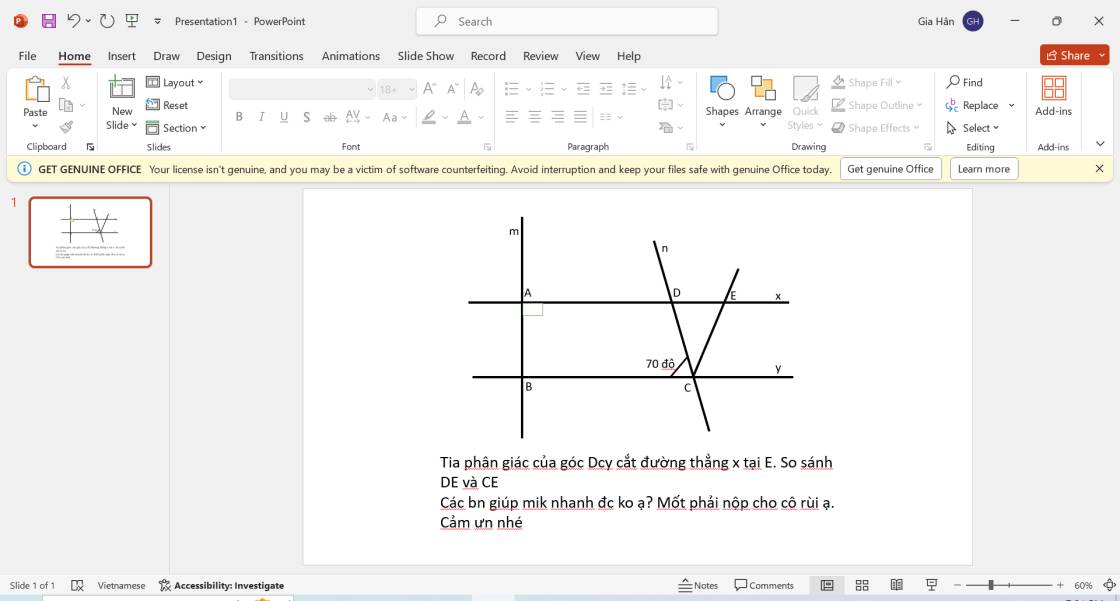
Ta có \(\widehat{CDE}\) = \(\widehat{DCB}\) = 70⁰ (hai góc so le trong)

         \(\widehat{DCY}\) + \(\widehat{BCD}\) = 180⁰ (hai góc kề bù)

       ⇒ \(\widehat{BCD}\) = 180⁰ - 70⁰ = 110⁰

         \(\widehat{DCE}\) = \(\dfrac{1}{2}\) \(\widehat{DCy}\) (CE là phân giác góc\(\widehat{DCy}\))

          \(\widehat{DCE}\) = 110⁰ x \(\dfrac{1}{2}\) = 55⁰

         \(\widehat{DEC}\) + \(\widehat{EDC}\) + \(\widehat{DCE}\) = 180⁰

         \(\widehat{DEC}\) = 180⁰ - 55⁰ - 70⁰

         \(\widehat{DEC}\) =  55⁰

         ⇒ \(\widehat{DEC}\) = \(\widehat{DCE}\) = 55⁰ 

          ⇒ \(\Delta\) DCE cân tại D ⇒DC = DE 

7,340 tấn nhé bạn

7 tấn 340 kg = 7,34 tấn

Cho like

Câu 2

Do n là số tự nhiên

\(\Rightarrow\) n chẵn hoặc n lẻ

*) n lẻ:

\(\Rightarrow13n\) lẻ

\(\Rightarrow13n+2023\) chẵn

\(\Rightarrow\left(13n+2023\right)⋮2\)

\(\Rightarrow\left(71n+2020\right).\left(13n+2023\right)⋮2\) (1)

*) n chẵn:

\(\Rightarrow71n\) chẵn

\(\Rightarrow71n+2020\) chẵn

\(\Rightarrow\left(7n+2020\right)⋮2\)

\(\Rightarrow\left(71n+2020\right)\left(13n+2023\right)⋮2\)  (2)

Từ (1) và (2) \(\Rightarrow\left(71n+2020\right)\left(13n+2023\right)⋮2\) với mọi n là số tự nhiên

Câu 1:

Gọi \(a\) (ngày) là số ngày ít nhất ba bạn lại cùng đến thư viện \(\left(a\in N\right)\)

\(\Rightarrow a=BCNN\left(5;8;10\right)\)

Ta có:

\(5=5\)

\(8=2^3\)

\(10=2.5\)

\(\Rightarrow a=BCNN\left(5;8;10\right)=2^3.5=40\)

Vậy sau 40 ngày thì ba bạn lại cùng đến thư viện

b) Do \(40:7=5\) (dư 5)

\(\Rightarrow\) Lần tiếp theo cả hai bạn cùng đến thư viện vào ngày thứ sáu

7960204e+168