2023.(16 - 2024) + 2024.2023 - 16.(2023 + 10)

= 2023.16 - 2023.2024 + 2024.2023 - 16.2023 - 16.10

= (2023.16 - 16.2023) - (2023.2024 - 2024.2023) - 16.10

= 0 - 0 - 16.10

= - 160 

\(2023.\left(16-2024\right)+2024.2023-16.\left(2023+10\right)\)

\(=2023.16-2023.2024+2023.2024-16.2023-16.10\)

\(=2023\left(16-16\right)+2023\left(2024-2024\right)-16.10\)

\(=0+0-160=-160\)

\(2023,24\times97+2023,24+4046,48\)

\(=2023,24\times97+2023,24+2023,24\times2\)

\(=2323,24\times\left(97+1+2\right)\)

\(=2023,24\times100\)

\(=202324\)

\(3n+10⋮n-1\Rightarrow3n-3+13⋮n-1\)

\(\Rightarrow3\left(n-1\right)+13⋮n-1\)

Do \(3\left(n-1\right)⋮n-1\Rightarrow13⋮n-1\)

\(\Rightarrow n-1=Ư\left(13\right)=\left\{-13;-1;1;13\right\}\)

\(\Rightarrow n=\left\{-12;0;2;14\right\}\)

Do n là số tự nhiên \(\Rightarrow n=\left\{0;2;14\right\}\)

Gọi \(d=ƯC\left(n+3;2n+5\right)\) với \(d\in N\)

\(\Rightarrow\left\{{}\begin{matrix}n+3⋮d\\2n+5⋮d\end{matrix}\right.\) \(\Rightarrow2\left(n+3\right)-\left(2n+5\right)⋮d\)

\(\Rightarrow1⋮d\Rightarrow d=1\)

Vậy \(n+3\) và \(2n+5\) nguyên tố cùng nhau với mọi số tự nhiên n

Gọi d = ƯCLN(n + 3, 2n + 50 với d ∈ N

$\Rightarrow \{\begin{array}{c}n+3⋮d\\ 2n+5⋮d\end{array}$ $\Rightarrow 2\left(n+3\right)-\left(2n+5\right)⋮d$

$\Rightarrow 1⋮d\Rightarrow d=1$

Vậy $n+3$ và $2n+5$ nguyên tố cùng nhau với mọi số tự nhiên n

Gọi \(d=ƯC\left(2n+3;4n+8\right)\) với \(d\in N\)

Do \(2n+3\) luôn lẻ \(\Rightarrow d\) lẻ

\(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\) \(\Rightarrow4n+8-2\left(2n+3\right)⋮d\)

\(\Rightarrow2⋮d\Rightarrow\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)

Mà d lẻ \(\Rightarrow d=1\)

Vậy 2n+3 và 4n+8 nguyên tố cùng nhau với mọi \(n\in N\)

Gọi \(d=ƯC\left(n+1;2n+3\right)\) với \(d\in N\)

\(\Rightarrow\left\{{}\begin{matrix}n+1⋮d\\2n+3⋮d\end{matrix}\right.\) \(\Rightarrow2n+3-2\left(n+1\right)⋮d\)

\(\Rightarrow1⋮d\Rightarrow d=1\)

Vậy n+1 và 2n+3 nguyên tố cùng nhau với mọi \(n\in N\)

Cứ 1 tia chung gốc sẽ tạo với 2021 - 1 tia còn lại số góc là: 2021 - 1 (góc)

Với 2021 tia chung gốc tạo được số góc là: (2021 - 1) x 2021 (góc)

Theo cách tính trên mỗi góc được tính hai lần nên số góc thực tế được tạo từ 2021 tia trong đó không có bất cứ hai tia nào đối nhau là:

       (2021 - 1) x 2021: 2 = 2041210 (góc)

Kết luận:..

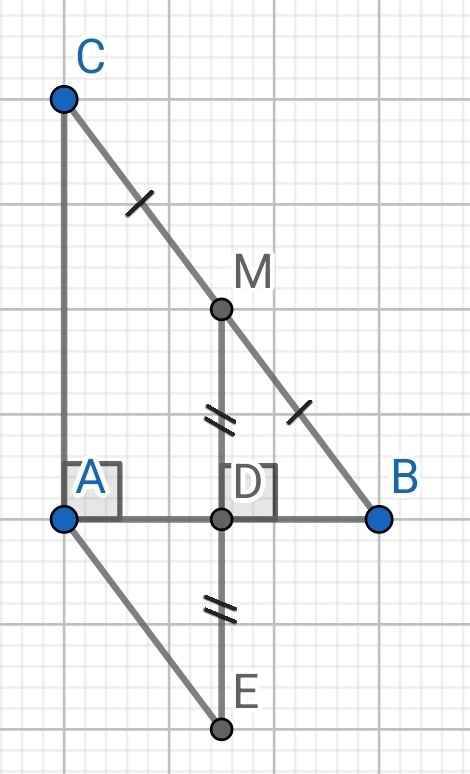 a) Do ∆ABC vuông tại A (gt)

⇒ AB ⊥ AC

Mà MD ⊥ AB (gt)

⇒ AC // MD

⇒ ADMC là hình thang

Mà ∠CAD = 90⁰ (∆ABC vuông tại A)

⇒ ADMC là hình thang vuông

b) ∆ABC có:

M là trung điểm của BC (gt)

MD // AC (cmt)

⇒ D là trung điểm của AB

⇒ MD là đường trung bình của ∆ABC

⇒ MD = AC : 2

⇒ AC = 2MD (1)

Do M và E đối xứng qua D

⇒ D là trung điểm của ME

⇒ ME = 2MD (2)

Từ (1) và (2) ⇒ AC = ME

Do AC // MD (cmt)

⇒ AC // ME

Tứ giác ACME có:

AC // ME (cmt)

AC = ME (cmt)

⇒ ACME là hình bình hành