Một phân xưởng mộc có 30 người được giao nhiệm vụ đóng một lô bàn ghế trong 8 ngày,mỗi ngày làm việc 8 giờ.Sau 2 ngày làm việc thì có 18 người được điều đi làm việc khác và số còn lại tăng thời gian làm việc mỗi ngày thêm 2 giờ.Hỏi phân xưởng đó hoàn thành khối lượng công việc được giao trong bao nhiêu ngày?Biết năng suất làm việc của mỗi người như nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cần tìm là \(26:\dfrac{2}{3}=26\cdot\dfrac{3}{2}=39\)

p: \(30x-3x=5\cdot54\)
=>\(27x=270\)
=>\(x=\dfrac{270}{27}=10\)
q: 3(x-2)+2(x+5)=29
=>3x-6+2x+10=29
=>5x+4=29
=>5x=25
=>\(x=\dfrac{25}{5}=5\)
t: (27-3x)(x-5)=0
=>3(9-x)(x-5)=0
=>(9-x)(x-5)=0
=>\(\left[{}\begin{matrix}9-x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=5\end{matrix}\right.\)
v: x+(x+1)+...+(x+30)=1240
=>31x+(1+2+...+30)=1240
=>\(31x+30\cdot\dfrac{31}{2}=1240\)
=>\(31\left(x+15\right)=31\cdot40\)
=>x+15=40
=>x=40-15=25
s: (x+2)+(4x+4)+(7x+6)+...+(25x+18)+(28x+20)=1560
=>(x+4x+7x+...+25x+28x)+(2+4+6+...+20)=1560
=>\(x\left(1+4+...+28\right)+2\left(1+2+3+...+10\right)=1560\)
=>\(x\left[\left(\dfrac{28-1}{3}+1\right)\cdot\dfrac{\left(28+1\right)}{2}\right]+2\cdot\dfrac{10\cdot11}{2}=1560\)
=>\(x\left[10\cdot\dfrac{29}{2}\right]+10\cdot11=1560\)
=>\(145x=1560-110=1450\)
=>x=10

Chiều dài mảnh vườn thứ ba là: \(\dfrac{65}{12}-\dfrac{25}{6}=\dfrac{65}{12}-\dfrac{50}{12}=\dfrac{15}{12}=\dfrac{5}{4}\left(m\right)\)
Chiều dài mảnh vườn thứ nhất là:
\(\dfrac{65}{12}-\dfrac{15}{4}=\dfrac{65}{12}-\dfrac{45}{12}=\dfrac{20}{12}=\dfrac{5}{3}\left(m\right)\)
Chiều dài mảnh vườn thứ hai là:
\(\dfrac{25}{6}-\dfrac{5}{3}=\dfrac{25}{6}-\dfrac{10}{6}=\dfrac{15}{6}=\dfrac{5}{2}\left(m\right)\)

a: \(\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
\(=6ab^2\)
b: \(\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3-8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x-9+3x^2-3=-3x-12\)

a: \(2^x+2^{x+4}=544\)
=>\(2^x+2^x\cdot16=544\)
=>\(17\cdot2^x=544\)
=>\(2^x=32=2^5\)
=>x=5
b: \(4^{2x+1}+4^{2x}=80\)
=>\(4^{2x}\cdot4+4^{2x}=80\)
=>\(4^{2x}\cdot5=80\)
=>\(4^{2x}=16=4^2\)
=>2x=2
=>x=1
c: \(3^{2x+2}+3^{2x+1}=108\)
=>\(3^{2x}\cdot9+3^{2x}\cdot3=108\)
=>\(12\cdot3^{2x}=108\)
=>\(3^{2x}=9=3^2\)
=>2x=2
=>x=1
d: \(7^{x+3}-7^{x+1}=16464\)
=>\(7^x\cdot343-7^x\cdot7=16464\)
=>\(7^x\cdot336=16464\)
=>\(7^x=49=7^2\)
=>x=2

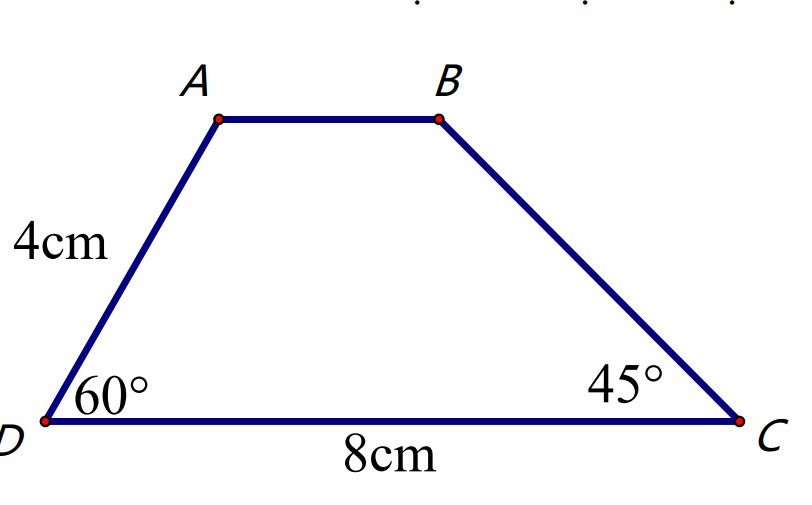
Dựng \(AH\perp CD;BK\perp CD\left(H;K\in CD\right)\)
Xét tg vuông ADH có
\(\widehat{DAH}=90^o-\widehat{D}=30^o\)
\(\Rightarrow DH=\dfrac{AD}{2}=\dfrac{4}{2}=2cm\) (trong tg vuông cạnh đối diện góc \(30^o\) băng nửa cạnh huyền)
\(\Rightarrow AH=\sqrt{AD^2-DH^2}=\sqrt{16-4}=\sqrt{12}=2\sqrt{3}cm\)
\(\Rightarrow AH=BK=2\sqrt{3}cm\) (đường cao của hình thang)
Xét tg vuông BCK có
\(\widehat{KBC}=90^o-\widehat{C}=45^o\)
=> tg BCK vuông cân tại K \(\Rightarrow CK=BK=2\sqrt{3}cm\)
\(\Rightarrow BC=\sqrt{BK^2+CK^2}=\sqrt{12+12}=2\sqrt{6}cm\)
Xét HCN ABKH có
\(AB=KH=CD-DH-CK=8-2\sqrt{3}-2\sqrt{3}=8-4\sqrt{3}=4\left(2-\sqrt{3}\right)cm\)

1/3 tuổi của Hải 4 năm trước bằng 1/4 tuổi của Hải 4 năm sau
=>\(\dfrac{1}{3}-\dfrac{1}{4}\) số tuổi của Hải năm nay là \(\dfrac{1}{4}\times4+\dfrac{1}{3}\times4=1+\dfrac{4}{3}=\dfrac{7}{3}\)
Tuổi của Hải năm nay là \(\dfrac{7}{3}:\dfrac{1}{12}=\dfrac{7}{3}\times12=28\left(tuổi\right)\)

1: \(x^2-25=\left(x-5\right)\left(x+5\right)\)
2: \(9x^2-\dfrac{1}{16}y^2=\left(3x\right)^2-\left(\dfrac{1}{4}y\right)^2\)
\(=\left(3x-\dfrac{1}{4}y\right)\left(3x+\dfrac{1}{4}y\right)\)
3: \(x^6-y^4=\left(x^3\right)^2-\left(y^2\right)^2=\left(x^3-y^2\right)\left(x^3+y^2\right)\)
4: \(\left(2x-5\right)^2-64=\left(2x-5-8\right)\left(2x-5+8\right)\)
\(=\left(2x-13\right)\left(2x+3\right)\)
5: \(81-\left(3x+2\right)^2\)
\(=\left(9-3x-2\right)\left(9+3x+2\right)\)
\(=\left(-3x+7\right)\left(3x+11\right)\)
6: \(9\left(x-5y\right)^2-16\left(x+y\right)^2\)
\(=\left(3x-15y\right)^2-\left(4x+4y\right)^2\)
\(=\left(3x-15y-4x-4y\right)\left(3x-15y+4x+4y\right)\)
\(=\left(-x-19y\right)\left(7x-11y\right)\)
7: \(x^3-8=x^3-2^3=\left(x-2\right)\left(x^2+2x+4\right)\)
8: \(27x^3+125y^3=\left(3x\right)^3+\left(5y\right)^3\)
\(=\left(3x+5y\right)\left(9x^2-15xy+25y^2\right)\)
9: \(x^6+216=\left(x^2\right)^3+6^3\)
\(=\left(x^2+6\right)\left(x^4-6x^2+36\right)\)
10: \(x^2+8x+16=x^2+2\cdot x\cdot4+4^2=\left(x+4\right)^2\)
11: \(9x^2-12xy+4y^2\)
\(=\left(3x\right)^2-2\cdot3x\cdot2y+\left(2y\right)^2\)
\(=\left(3x-2y\right)^2\)
12: \(-25x^2y^2+10xy-1\)
\(=-\left[\left(5xy\right)^2-2\cdot5xy\cdot1+1^2\right]\)
\(=-\left(5xy-1\right)^2\)
13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)

BM+MN+NC=BC
=>\(BC=MN+\dfrac{2}{3}MN+\dfrac{1}{2}MN=\dfrac{13}{6}MN\)
=>\(\dfrac{BM}{BC}=\dfrac{2}{3}:\dfrac{13}{6}=\dfrac{2}{3}\cdot\dfrac{6}{13}=\dfrac{12}{39}=\dfrac{4}{13}\)
=>BC=3,25BM
\(S_{ABM}=\dfrac{1}{2}\cdot MH\cdot AB=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)
BC=3,25BM nên \(S_{ABC}=3,25\cdot S_{ABM}=3,25\cdot150=487,5\left(cm^2\right)\)