Tắm giác ABC .Trên AB lấy AD=2BC,AB=2EC Với CD cắt BE tại I.So sánh diện tơch BDI và CIE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\\ =x^3-xy-x^3-x^2y+x^2y-xy\\ =-2xy\)
Thay `x=1/2;y=-100` vào A ta có:
\(A=-2\cdot\dfrac{1}{2}\cdot\left(-100\right)=100\)
\(B=\left(x^2-5\right)\left(x+3\right)+\left(x+4\right)\left(x-x^2\right)\\=x^3+3x^2-5x-15-x^3+4x+x^2-4x^2\\ =\left(x^3-x^3\right)+\left(3x^2-4x^2+x^2\right)+\left(-5x+4x\right)-15\\ =-x-15\)


\(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}=1,2\\\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=1,2-8\dfrac{1}{5}\\ \Rightarrow \left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=-7\)
Nhận xét:
\(\left\{{}\begin{matrix}\left|2\dfrac{1}{5}-x\right|\ge0,\forall x\\\left|x-\dfrac{1}{5}\right|\ge0,\forall x\end{matrix}\right.\\
\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|\ge0,\forall x\)
Mà \(-7< 0\) nên:
Không tìm được giá trị \(x\) thỏa mãn đề bài
Vậy...

\(\left\{{}\begin{matrix}2x+3y=-xy\\\dfrac{8}{x}-\dfrac{6}{y}=5\end{matrix}\right.\left(x;y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\8y-6x=5xy\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=-5xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=5\left(2x+3y\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=10x+15y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\-4x=23y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{-23}{4}y+3y=\dfrac{-23}{4}y\cdot y\\x=\dfrac{-23}{4}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23y^2-43y=0\\x=\dfrac{-23}{4}y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y\left(23y-43\right)=0\\x=\dfrac{-23}{4}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=0\left(ktm\right)\\y=\dfrac{43}{23}\left(tm\right)\end{matrix}\right.\\x=\dfrac{-23}{4}\cdot\dfrac{43}{23}=\dfrac{-43}{4}\end{matrix}\right.\)

bài giải
số lớn chia số bé được 3 dư 3, số bé bằng 1/3 số lớn
số lớn là:
33 : ( 3 -1 ) x 3 + 3 = 53,5
số bé là:
33: ( 3 - 1 ) = 16,5
đ/s

Gọi chiều dài là a => chiều rộng = a-4
Theo bài ra: a+(a-4)=80
<=> 2a = 84
=> a = 42
=> chiều rộng = a-4 = 42-4 = 38
Diện tích tấm màn là: 38x42= 1596 m2

\(\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}=9\\\dfrac{1}{\sqrt{x^2+1}}-\dfrac{1}{\sqrt{y^2+1}}=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}=9\\\dfrac{4}{\sqrt{x^2+1}}-\dfrac{4}{\sqrt{y^2+1}}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}+\dfrac{4}{\sqrt{x^2+1}}-\dfrac{4}{\sqrt{y^2+1}}=9+3\\\dfrac{1}{\sqrt{x^2+1}}-\dfrac{1}{\sqrt{y^2+1}}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{12}{\sqrt{x^2+1}}=12\\\dfrac{1}{\sqrt{y^2+1}}=1-\dfrac{3}{4}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+1=1\\y^2+1=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2=0\\y^2=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\pm\sqrt{15}\end{matrix}\right.\)
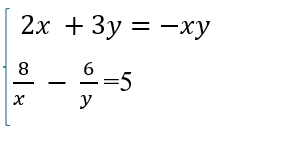
minhf cũng đang hỏi bài này luôn nè.