a) Do H và K đối xứng nhau qua I

⇒ I là trung điểm của HK

Do AH là đường cao của ∆ABC

⇒ AH ⊥ BC

⇒ ∠AHB = 90⁰

Tứ giác AHBK có:

I là trung điểm HK (cmt)

I là trung điểm AB (gt)

⇒ AHBK là hình bình hành

Mà ∠AHB = 90⁰ (cmt)

⇒ AHBK là hình chữ nhật

b) ∆ABC cân tại A (gt)

AH là đường cao

⇒ AH cũng là đường trung tuyến của ∆ABC

⇒ H là trung điểm BC

Mà I là trung điểm AB (gt)

⇒ HI là đường trung bình của ∆ABC

⇒ HI // AC

Tứ giác ACHI có:

HI // AC (cmt)

⇒ ACHI là hình thang

c) ∆ABC đều

⇒ ∠BAC = ∠ACB = 60⁰

⇒ ∠IAC = ∠ACH = 60⁰

Mà ACHI là hình thang (cmt)

⇒ ACHI là hình thang cân

 Sửa đề:

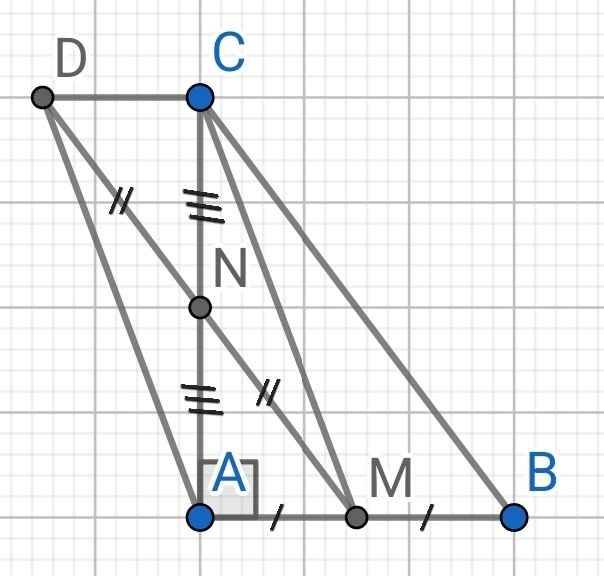
a) Chứng minh tứ giác BMDC là hình bình hành

b) Tứ giác AMCD là hình gì? Vì sao?

GIẢI

a) Do M là trung điểm AB

N là trung điểm AC

⇒ MN là đường trung bình của ∆ABC

⇒ MN // BC và MN = BC : 2

Do MN // BC (cmt)

⇒ MD // BC

Ta có:

ND = NM (gt)

⇒ MN = MD : 2

Mà MN = BC : 2 (cmt)

⇒ MD = BC

Tứ giác BMDC có:

MD // BC (cmt)

MD = BC (cmt)

⇒ BMDC là hình bình hành

b) Do BMDC là hình bình hành (cmt)

⇒ BM // CD và BM = CD

⇒ AM // CD

Lại có:

M là trung điểm của AB (gt)

⇒ AM = BM = AB : 2

Mà BM = CD (cmt)

⇒ AM = CD

Tứ giác AMCD có:

AM // CD (cmt)

AM = CD (cmt)

⇒ AMCD là hình bình hành

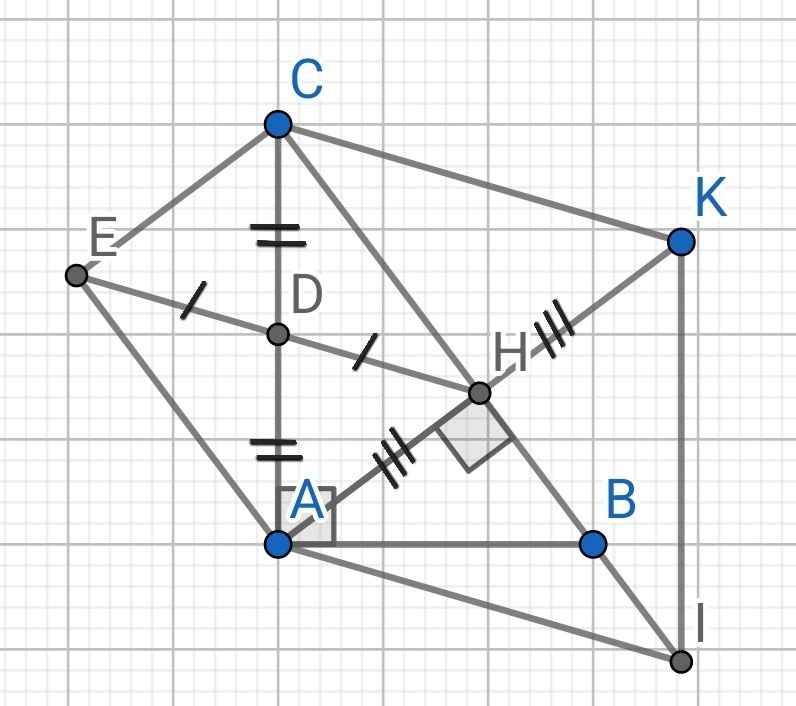a) Do AH là đường cao của ∆ABC

⇒ AH ⊥ BC

⇒ ∠AHC = 90⁰

Tứ giác AHCE có:

D là trung điểm AC (gt)

D là trung điểm HE (gt)

⇒ AHCE là hình bình hành

Mà ∠AHC = 90⁰ (cmt)

⇒ AHCE là hình chữ nhật

b) Do AHCE là hình chữ nhật (cmt)

⇒ AE // HC

⇒ AE // HI

Tứ giác AEIH có:

AE // HI (cmt)

AI // HE (gt)

⇒ AEIH là hình bình hành

c) Do AHCE là hình chữ nhật (cmt)

⇒ AC = HE

Do AEIH là hình bình hành (cmt)

⇒ HE = AI

⇒ AC = AI

⇒ ∆ACI cân tại A

Lại có:

AH ⊥ BC (cmt)

⇒ AH ⊥ CI

AH là đường cao của ∆ACI

⇒ AH cũng là đường trung tuyến của ∆ACI

⇒ H là trung điểm của CI

Do HA = HK (gt)

⇒ H là trung điểm của AK

Do AH ⊥ CI (cmt)

⇒ AH ⊥ CK

Tứ giác ACKI có:

H là trung điểm CI (cmt)

H là trung điểm của AK (cmt)

⇒ ACKI là hình bình hành

Mà AK ⊥ CI (cmt)

⇒ ACKI là hình thoi

⇒ AK là tia phân giác của ∠IAC

d) Để CAIK là hình vuông thì AC ⊥ AI

Mà AC ⊥ AB và AC = AI

⇒ AC = AB (B ≡ I)

⇒ ∆ABC vuông cân tại A

⇒ AH vừa là đường cao, vừa là đường trung tuyến của ∆ABC

⇒ AH = HC = BC : 2

Mà tứ giác AHCE là hình chữ nhật có AH = HC

⇒ AHCE là hình vuông

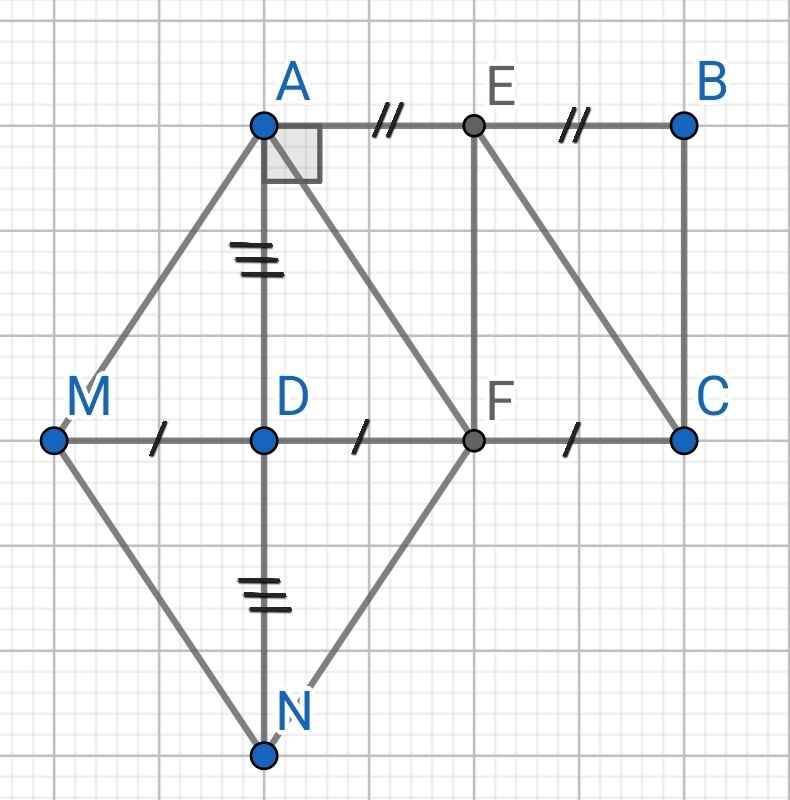 a) Do ABCD là hình chữ nhật (gt)

⇒ AB = CD (1)

Do E là trung điểm của AB

⇒ AE = BE = AB : 2 (2)

Do F là trung điểm của CD (gt)

⇒ CF = DF = CD : 2 (3)

Từ (1), (2) và (3) ⇒ AE = CF

Do ABCD là hình chữ nhật (gt)

⇒ AB // CD

⇒ AE // CF

Tứ giác AECF có:

AE // CF (cmt)

AE = CF (cmt)

⇒ AECF là hình bình hành

b) Do AE = CF (cmt)

CF = DF (cmt)

⇒ AE = DF

Do AB // CD (cmt)

⇒ AE // DF

Tứ giác AEFD có:

AE // DF (cmt)

AE = DF (cmt)

⇒ AEFD là hình bình hành

Mà ∠DAE = 90⁰ (gt)

⇒ AEFD là hình chữ nhật

c) Do ABCD là hình chữ nhật (gt)

⇒ AB ⊥ CD

⇒ AN ⊥ MF

Tứ giác AMNF có:

D là trung điểm của AN (gt)

D là trung điểm của MF (gt)

⇒ AMNF là hình bình hành

Mà AN ⊥ MF (cmt)

⇒ AMNF là hình thoi

a) \(A=x^2-25\)

\(A=x^2-5^2\)

\(A=\left(x+5\right)\left(x-5\right)\)

Thay x = 105 vào ta có:

\(A=\left(105+5\right)\left(105-5\right)=110\cdot100=11000\)

b) \(B=x^2-4y^2+x-2y\)

\(B=\left(x-2y\right)\left(x+2y\right)+\left(x-2y\right)\)

\(B=\left(x-2y\right)\left(x+2y+1\right)\)

Thay \(x+2y=-1\) vào ta có:

\(B=\left(x-2y\right)\left(-1+1\right)=\left(x-2y\right)\cdot0=0\)

a) \(3\left(x+1\right)+5x=0\)

\(\Leftrightarrow3x+3+5x=0\)

\(\Leftrightarrow8x=-3\)

\(\Leftrightarrow x=-\dfrac{3}{8}\)

b) \(4x^2-1-\left(2x+1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\2x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\) 

c) \(\left(x+1\right)^2+x^2-1=0\)

\(\Leftrightarrow\left(x+1\right)^2+\left(x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x+1+x-1\right)=0\)

\(\Leftrightarrow\left(x+1\right)2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

d) \(\left(x+2\right)\left(x-2\right)+x\left(x-3\right)-2x^2=8\)

\(\Leftrightarrow x^2-4+x^2-3x-2x^2=8\)

\(\Leftrightarrow-3x-4=8\)

\(\Leftrightarrow-3x=8+4\)

\(\Leftrightarrow-3x=12\)

\(\Leftrightarrow x=-4\)

a) \(x^2-4x^2y^2+y^2+2xy\)

\(=\left(x^2+2xy+y^2\right)-\left(2xy\right)^2\)

\(=\left(x+y\right)^2-\left(2xy\right)^2\)

\(=\left(x-2xy+y\right)\left(x+2xy+y\right)\)

b) \(x^3-x^2y+4x-4y\)

\(=x^2\left(x-y\right)+4\left(x-y\right)\)

\(=\left(x^2+4\right)\left(x-y\right)\)

c) \(x^2+12y-36-y^2\)

\(=x^2-\left(y^2-12y+36\right)\)

\(=x^2-\left(y-6\right)^2\)

\(=\left(x+y-6\right)\left(x-y+6\right)\)

d) \(4x\left(x+y\right)\left(x+y+z\right)\left(x+z\right)+y^2z^2\)

\(=4\left(x^2+xy+xz\right)\left(x^2+xy+xz+yz\right)+y^2z^2\)

\(=4\left(x^2+xy+xz\right)^2+4yz\left(x^2+xy+xz\right)+\left(yz\right)^2\)

\(=\left(2x^2+2xy+2xz+yz\right)^2\)

a, \(x^2\) - 4\(x^2\).y² + y² + 2\(xy\)

 = (\(x^2\) + 2\(xy\) + y²) - (2\(xy\))²

= (\(x\) + y)² - (2\(xy\))²

= (\(x\) + y  - 2\(xy\)).(\(x\) + y + 2\(xy\))

a) \(x\left(x+2\right)-2x\)

\(=x^2+2x-2x\)

\(=x^2\)

b) \(\left(2+x\right)\left(2-x\right)+x^2\)

\(=\left(4-x^2\right)+x^2\)

\(=4-x^2+x^2\)

\(=4\)

c) \(x^2\left(1-x\right)+\left(x+3\right)\left(x^2-3x+9\right)\)

\(=x^2-x^3+x^3+27\)

\(=x^2+27\)

d) \(\left(2x+y\right)^2+4x^2-4x\left(2x+y\right)\)

\(=4x^2+4xy+y^2+4x^2-8x^2-4xy\)

\(=8x^2-8x^2+4xy-4xy+y^2\)

\(=y^2\)

a/

Ta có

HI=CI (gt); AI=KI (gt) => ACKH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

=> AC//HK (Trong hbh 2 cạnh đối // với nhau)

b/

Ta có

\(HM\perp AB\left(gt\right);AC\perp AB\left(gt\right)\) => HM//AC

Mà HK//AC (cmt)

\(\Rightarrow HM\equiv HK\) (Từ 1 điểm ở ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho) => M; K; H thẳng hàng

=> AC//MK => MNCK là hình thang

Ta có

AC//MK => AN//MH

\(AB\perp AC\left(gt\right);HN\perp AC\left(gt\right)\) => AB//HN => AM//HN

=> AMHN là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

\(\widehat{A}=90^o\)

=> AMHN là hình chữ nhật => AH=MN (trong HCN hai đường chéo bằng nhau)

Mà ACKH là hbh (cmt) => AH=CK (cạnh đối hbh)

=> MN=CK

=> hình thang MNCK có MN = CK => MNCK là hình thang cân

c/

Xét tg AHC có

OA=OH (Trong hình chữ nhật 2 đường chéo cắt nhau tại trung điểm mỗi đường)

HI=CI (gt)

=> D là trọng tâm của tg AHC \(\Rightarrow AD=\dfrac{2}{3}AI\)

Xét hình bình hành ACKH có

\(AI=KI\) (Trong hình bh 2 đường chéo cắt nhau tại trung điểm mỗi đường) \(\Rightarrow AI=\dfrac{1}{2}AK\)

\(\Rightarrow AD=\dfrac{2}{3}.\dfrac{1}{2}AK=\dfrac{1}{3}AK\Rightarrow AK=3AD\)

Thực hiện phép chia \(f(x)\) cho \(x-1\), ta được:

\(f(x)=(x-1)\cdot Q(x)+r\\\Rightarrow f(1)=(1-1)\cdot Q(1)+r\\\Rightarrow f(1)=r\\\Rightarrow 1^{100}+1^{99}+1^{98}+1^{97}+...+1+1=r\\\Rightarrow r=101(101.chữ.số.1)\)

Vậy số dư của phép chia $f(x)$ cho $(x-1)$ là 101.