Mọi người giúp em bài này với ạ, mn giải chi tiết giúp em nha, cảm ơn mn

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(a² + b² + c²).(1+1+1) ≥ (a.1 + b.1 + c.1)² = 1
=> a² + b² + c² ≥ 1/3
dấu "=" xảy ra <=> a/1 = b/1 = c/1 => a = b = c = 1/

Lời giải:
a. Bạn tự vẽ
b. Gọi ptđt $(D)$ là $y=ax+b$. Vì $A\in (D)$ nên:
$y_A=ax_A+b\Leftrightarrow -3=a+b(1)$
$(D)$ tiếp xúc với $(P)$
$\Leftrightarrow$ phương trình hoành độ giao điểm $x^2-ax-b=0$ có nghiệm kép
$\Leftrightarrow \Delta=a^2+4b=0(2)$
Từ $(1); (2)\Rightarrow a=6$ hoặc $a=-2$
Nếu $a=6$ thì $b=-3-a=-9$.
Nếu $a=-2$ thì $b=-3-a=-3-(-2)=-1$
Vậy ptđt $(D)$ là $y=6x-9$ hoặc $y=-2x-1$
c.
PT hoành độ giao điểm của $(d)$ và $(P)$:
$x^2-(2-m)x-(m-1)=0$
Để $(P)$ và $(d)$ cắt nhau tại 2 điểm pb thì:
$\Delta=(2-m)^2+4(m-1)>0\Leftrightarrow m^2>0\Leftrightarrow m\neq 0$
Áp dụng định lý Viet:
$x_1+x_2=2-m$
$x_1x_2=-(m-1)=1-m$
$\Rightarrow x_1x_2-x_1-x_2=-1$
$\Leftrightarrow x_1x_2-x_1-x_2+1=0$
$\Leftrightarrow (x_1-1)(x_2-1)=0$
$\Leftrightarrow x_1=1$ hoặc $x_2=1$
Nếu $x_1=1$
$x_2^3-2x_1=64$
$\Leftrightarrow x_2^3-2=64\Leftrightarrow x_2^3=66$
$\Leftrightarrow x_2=\sqrt[3]{66}$
$2-m=x_1+x_2=1+\sqrt[3]{66}$
$\Leftrightarrow m=1-\sqrt[3]{66}$
Nếu $x_2=1$
$x_2^3-2x_1=64$
$\Leftrightarrow 1-2x_1=64$
$\Leftrightarrow x_1=\frac{-63}{2}$
$2-m=x_1+x_2=\frac{-63}{2}+1=\frac{-61}{2}$
$\Leftrightarrow m=\frac{65}{2}$

Ta thấy \(x>0\) nên ta có thể suy ra \(\sqrt{x}=\sqrt{4-2\sqrt{3}}\) \(=\sqrt{3-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}-1\right)^2}\) \(=\sqrt{3}-1\) (do \(\sqrt{3}-1>0\))
Từ đó \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) \(=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\) \(=\dfrac{\sqrt{3}}{\sqrt{3}-4}\) \(=\dfrac{\sqrt{3}\left(\sqrt{3}+4\right)}{\left(\sqrt{3}-4\right)\left(\sqrt{3}+4\right)}\) \(=\dfrac{3+4\sqrt{3}}{\left(\sqrt{3}\right)^2-4^2}\) \(=-\dfrac{3+4\sqrt{3}}{13}\)
Ta có : \(x\text{=}4-2\sqrt{3}\)
\(\Rightarrow x=3-2\sqrt{3}+1\)
\(\Rightarrow x=\left(\sqrt{3}-1\right)^2\)
\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-1\right)^2}\text{=}\sqrt{3}-1\)
Do đó :
\(Q\text{=}\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(Q\text{=}\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\)
\(Q\text{=}\dfrac{\sqrt{3}}{\sqrt{3}-4}\)
Chắc đến đây thôi nhỉ .

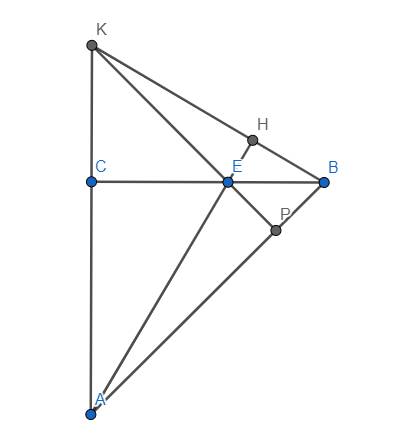
Do \(CA=CB=a\) nên \(BE.BC+AC.AK=a\left(AK+BE\right)\)
Ta chứng minh \(AK+BE\) không đổi. Thật vậy, gọi P là giao điểm của KE và AB. Quan sát thấy E là trực tâm tam giác ABK \(\Rightarrow KP\perp AP\) tại P. Lại có \(\widehat{KAP}=45^o\) nên suy ra \(\widehat{AKP}=45^o\). Từ đó suy ta tam giác CEK cân tại C hay \(CE=CK\).
Từ đó \(AK+BE=AC+CK+BC-CE=2a\). Vậy \(BE.BC+AC.AK=2a^2\) không đổi (đpcm)

Ta có : \(S_{ABC}=\dfrac{AH.BC}{2}\)
Kẻ đường cao từ B xuống AC tại E do đó :
\(S_{ABC}=\dfrac{BE.AC}{2}\)
mà \(BE< AB\) ( AB là cạnh huyền trong tam giác ABE )
Do đó :
\(\dfrac{AB.AC}{2}\ge\dfrac{BE.AC}{2}=\dfrac{AH.BC}{2}\)
\(\Rightarrow AB.AC\ge AH.BC\left(đpcm\right)\)
Dấu bằng xảy ra khi và chỉ khi : BE trùng với AB
\(\Leftrightarrow\Delta ABC\) vuông tại A .

ĐKXĐ : \(x\ge\dfrac{1}{2}\)
Đặt \(\sqrt{2x-1}=a;\sqrt{8x+1}=b\left(a;b\ge0\right)\)
=> \(a^2=2x-1;b^2=8x+1\Rightarrow\dfrac{a^2+b^2}{10}=x\)
Lại có \((13x+1).\sqrt{2x-1}=(7x-1).\sqrt{8x+1}-4\)
\(\Leftrightarrow-\left(\sqrt{2x-1}\right)^3+15x.\sqrt{2x-1}=-\left(\sqrt{8x+1}\right)^3+15x.\sqrt{8x+1}-4\)
\(\Leftrightarrow-a^3+15ax=-b^3+15bx-4\)
\(\Leftrightarrow a^3-b^3-\dfrac{3}{2}.\left(a-b\right).\left(a^2+b^2\right)=4\)
\(\Leftrightarrow-\left(a-b\right)^3=8\)
\(\Leftrightarrow a=b-2\)
Thay vào ta được : \(\sqrt{2x-1}=\sqrt{8x+1}-2\)
\(\Leftrightarrow3x+3=2\sqrt{8x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}9x^2-14x+5=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{9}\end{matrix}\right.\)(tm ĐKXĐ)

√4−√7−√4+√7+√7=√2(√4−√7−√4+√7+√7)√2=√8−2√7−√8+2√7+√14√2=√7−2√7+1−√7+2√7+1+√14√2=√(√7−1)2−√(√7+1)2+√14√2=∣∣√7−1∣∣−∣∣√7+1∣∣+√14√2=√7−1−√7−1+√14√2=√14−2√2=√2(√7−√2)√2=√7−√2
Lời giải:
\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}=\sqrt{\frac{8-2\sqrt{7}}{2}}-\sqrt{\frac{8+2\sqrt{7}}{2}}=\sqrt{\frac{(\sqrt{7}-1)^2}{2}}-\sqrt{\frac{(\sqrt{7}+1)^2}{2}}\)
\(=\frac{|\sqrt{7}-1|}{\sqrt{2}}-\frac{|\sqrt{7}+1|}{\sqrt{2}}=\frac{\sqrt{7}-1-(\sqrt{7}+1)}{\sqrt{2}}=\frac{-2}{\sqrt{2}}=-\sqrt{2}\)