giúp mình vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a\left(b^2+c^2\right)+b\left(c^2+a^2\right)+c\left(a^2+b^2\right)+3ab\\ =ab^2+ac^2+bc^2+ba^2+ca^2+cb^2+3abc\\ =\left(a^2b+ab^2+abc\right)+\left(bc^2+b^2c+abc\right)+\left(ca^2+ac^2+abc\right)\\ =ab\left(a+b+c\right)+bc\left(a+b+c\right)+ca\left(a+b+c\right)\\ =\left(a+b+c\right)\left(ab+bc+ca\right)\)

Bài 3:
\(a,\left(x-3\right)^3-x^2\left(x+2\right)+11x=-108\\ \Leftrightarrow x^3-9x^2+27x-27-x^3-2x^2+11x^2=-108\\ \Leftrightarrow-11x^2+27x-27+11x^2=-108\\ \Leftrightarrow27x-27=-108\\ \Leftrightarrow27x=-108+27\\ \Leftrightarrow27x=-81\\ \Leftrightarrow x=-\dfrac{81}{27}\\ \Leftrightarrow x=-3\\ b,\left(2x+3\right)^3-8x\left(x+1\right)\left(x-1\right)=9x\left(4x-3\right)\\ \Leftrightarrow\left(8x^3+36x^2+54x+27\right)-8x\left(x^2-1\right)=36x^2-27x\\ \Leftrightarrow8x^3+36x^2+54x+27-8x^3+8x=36x^2-27x\\ \Leftrightarrow36x^2+62x+27=36x^2-27x\\ \Leftrightarrow62x+27=-27x\\ \Leftrightarrow62x+27x=-27\\ \Leftrightarrow89x=-27\\ \Leftrightarrow x=\dfrac{-27}{89}\)
Bài 4:
a: \(18^3-3\cdot18^2\cdot8+3\cdot18\cdot8^2-2^9\)
\(=18^3-3\cdot18^2\cdot8+3\cdot18\cdot8^2-8^3\)
\(=\left(18-8\right)^3=10^3=1000\)
b: \(997^3+9\cdot997^2+997\cdot27+27\)
\(=997^3+3\cdot997^2\cdot3+3\cdot997\cdot3^2+3^3\)
\(=\left(997+3\right)^3=1000^3=10^9\)

\(x^4+6x^2+5x+6\\ =\left(x^4-x\right)+\left(6x^2+6x+6\right)\\ =x\left(x^3-1\right)+6\left(x^2+x+1\right)\\ =x\left(x-1\right)\left(x^2+x+1\right)+6\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left[x\left(x-1\right)+6\right]\\ =\left(x^2+x+1\right)\left(x^2-x+6\right)\)

\(x^4-10x^2-11x-10\\ =\left(x^4-x\right)+\left(-10x^2-10x-10\right)\\ =x\left(x^3-1\right)-10\left(x^2+x+1\right)\\ =x\left(x-1\right)\left(x^2+x+1\right)-10\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left[x\left(x-1\right)-10\right]\\ =\left(x^2+x+1\right)\left(x^2-x-10\right)\)

\(\left(a-x\right)y^3-\left(a-y\right)x^3+\left(x-y\right)a^3\\ =ay^3-xy^3-ax^3+x^3y+a^3x-a^3y\\ =\left(ay^3-ax^3\right)+\left(-xy^3+xy^3\right)+\left(a^3x-a^3y\right)\\ =a\left(y^3-x^3\right)+-xy\left(y^2-x^2\right)+a^3\left(x-y\right)\\ =a\left(y-x\right)\left(x^2+xy+y^2\right)-xy\left(y-x\right)\left(x+y\right)-a^3\left(y-x\right)\\ =\left(y-x\right)\left[a\left(x^2+xy+y^2\right)-xy\left(x+y\right)-a^3\right]\\ =\left(y-x\right)\left(ax^2+axy+ay^2-x^2y-xy^2-a^3\right)\)

\(x^3-5x^2+8x-4\\ =\left(x^3-x^2\right)+\left(-4x^2+4x\right)+\left(4x-4\right)\\ =x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x^2-4x+4\right)\left(x-1\right)\\ =\left[x^2-2\cdot x\cdot2+2^2\right]\left(x-1\right)\\ =\left(x-2\right)^2\left(x-1\right)\)

a: Ta có: BH\(\perp\)AC
CK\(\perp\)AC
Do đó: BH//CK
Ta có: CH\(\perp\)AB
BK\(\perp\)BA
Do đó: CH//BK
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
c: Xét ΔHIK có
G,M lần lượt là trung điểm của HI,HK
=>GM là đường trung bình của ΔHIK
=>GM//IK
=>BC//IK
Xét ΔCHI có
CG là đường cao
CG là đường trung tuyến
Do đó: ΔCHI cân tại C
=>CH=CI
mà CH=BK
nên BK=CI
Xét tứ giác BCKI có BC//KI và BK=CI
nên BCKI là hình thang cân

\(x^3-x^2-14x+24\\ =\left(x^3-2x^2\right)+\left(x^2-2x\right)+\left(-12x+24\right)\\ =x^2\left(x-2\right)+x\left(x-2\right)-12\left(x-2\right)\\ =\left(x-2\right)\left(x^2+x-12\right)\\ =\left(x-2\right)\left[\left(x^2-3x\right)+\left(4x-12\right)\right]\\ =\left(x-2\right)\left[x\left(x-3\right)+4\left(x-3\right)\right]\\ =\left(x-2\right)\left(x-3\right)\left(x+4\right)\)

\(1,A=x^2-12x+11\\ =\left(x^2-12x+36\right)-25\\ =\left(x-6\right)^2-25\)
Ta có: `(x-6)^2>=0` với mọi x
`=>(x-6)^2-25>=-25` với mọi x
Dấu "=" xảy ra: `x-6=0<=>x=6`
\(2,M=-4x^2+12x-7\\ =\left(-4x^2+12x-9\right)+2\\ =-\left(4x^2-12x+9\right)+2\\ =-\left(2x-3\right)^2+2\)
Ta có: `(2x-3)^2>=0` với mọi x
`=>-(2x-3)^2<=0` với mọi x
`=>-(2x-3)^2+2<=2` với mọi x
Dấu "=" xảy ra: `2x-3=0<=>x=3/2`
1: \(A=x^2-12x+11\)
\(=x^2-12x+36-25\)
\(=\left(x-6\right)^2-25>=-25\forall x\)
Dấu '=' xảy ra khi x-6=0
=>x=6
10: \(M=-4x^2+12x-7\)
\(=-4x^2+12x-9+2\)
\(=-\left(2x-3\right)^2+2< =2\forall x\)
Dấu '=' xảy ra khi 2x-3=0
=>2x=3
=>\(x=\dfrac{3}{2}\)

 giúp mình với
giúp mình với


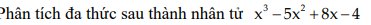


\(a,M=\left(x+1\right)^3-x^3+1-3x\left(x+1\right)\\ =x^3+3x^2+3x+1-x^3+1-3x^2-3x\\ =\left(x^3-x^3\right)+\left(3x^2-3x^2\right)+\left(3x-3x\right)+\left(1+1\right)\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến
\(b,\left(2x-1\right)^3-6x\left(2x-1\right)^2+12x^2\left(2x-1\right)-8x^3\\ =\left(2x-1\right)^3-3\cdot\left(2x-1\right)^2\cdot2x+3\cdot\left(2x-1\right)\cdot\left(2x\right)^2-\left(2x\right)^3\\ =\left(2x-1-2x\right)^3\\ =\left(-1\right)^3=-1\)
Vậy giá trị của bt không phụ thuộc vào biến
\(c,P=\left(x+y+1\right)^3-\left(x+y-1\right)^3-6\left(x+y\right)^2\\ =\left(x+y+1-x-y+1\right)\left[\left(x+y+1\right)^2+\left(x+y+1\right)\left(x+y-1\right)+\left(x+y-1\right)^2\right]-6\left(x+y\right)^2\\ =2\left[\left(x+y\right)^2+2\left(x+1\right)+1+\left(x+y\right)^2-1+\left(x+y\right)^2-2\left(x+y\right)+1\right]-6\left(x+y\right)^2\\ =2\left[3\left(x+y\right)^2+1\right]-6\left(x+y\right)^2\\ =6\left(x+y\right)^2+2-6\left(x+y\right)^2\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến