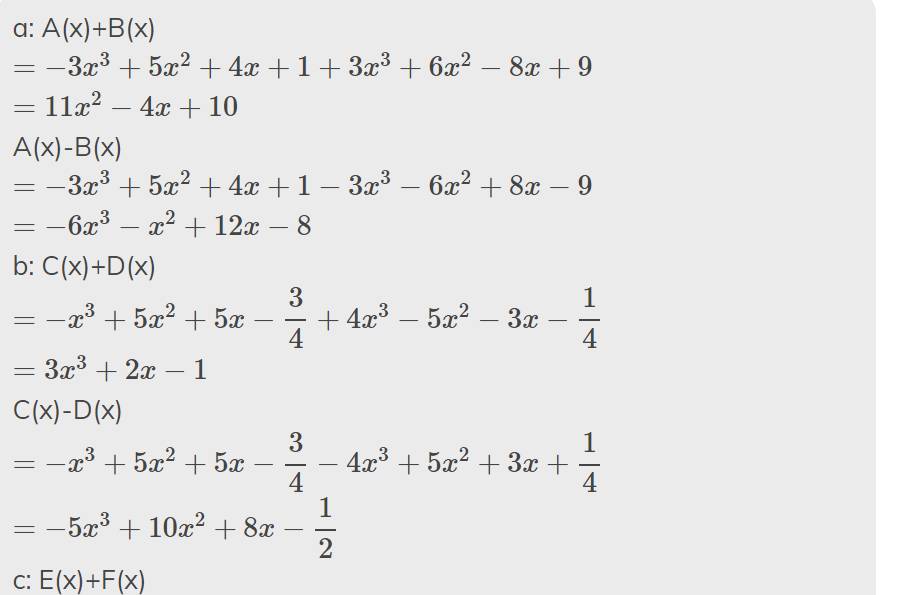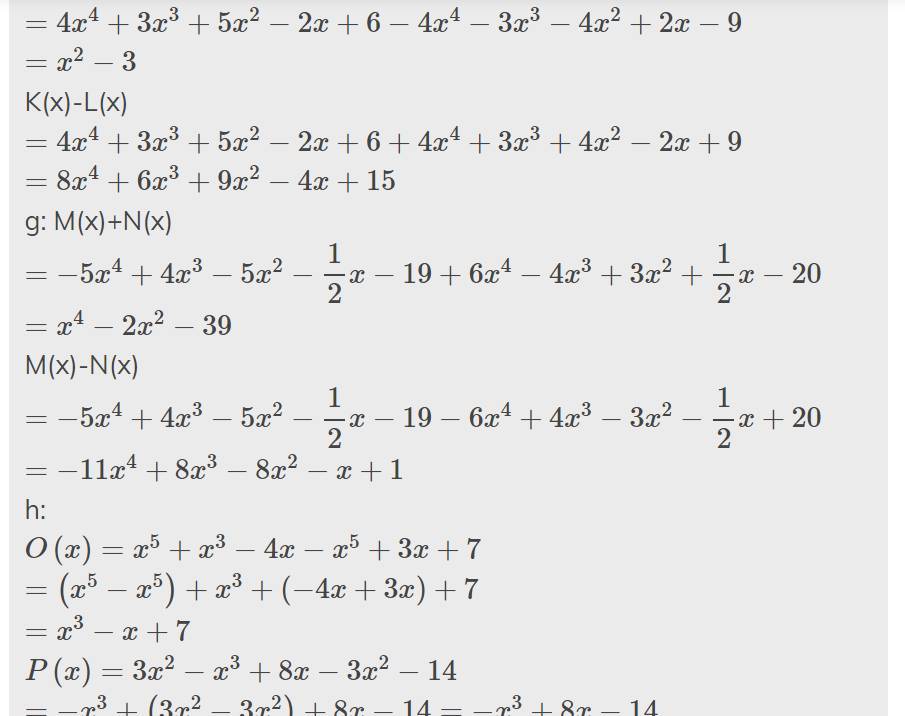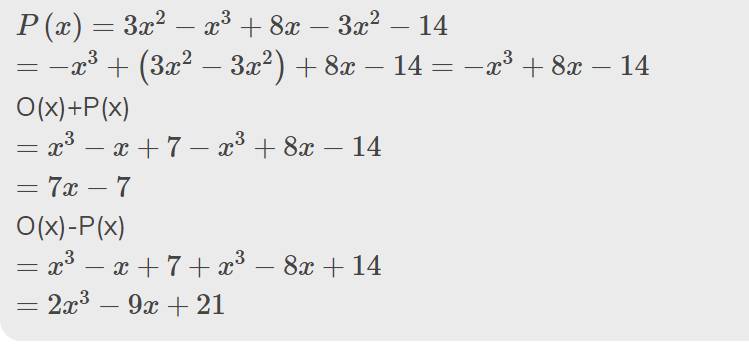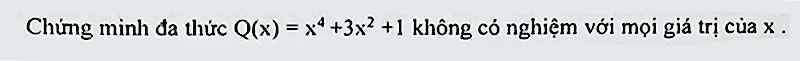Mn giúp em với cần gấp!!!
Mn giúp em với cần gấp!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(D=-16x^5-28x^4+16x^3-20x^2+32x+2016\)
\(=4x\left(-4x^4-7x^3+4x^2-5x+8\right)+2016\)
\(=4x\cdot0+2016=2016\)

D nằm trên đường trung trực của AB
=>DA=DB
D nằm trên đường trung trực của AC
=>DA=DC
Do đó: DA=DB=DC
=>D là tâm đường tròn ngoại tiếp ΔABC
ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà D là tâm của đường tròn ngoại tiếp ΔABC
nên D là trung điểm của BC

a; (2\(x-4\)).(\(x+9\)) = 0
\(\left[{}\begin{matrix}2x-4=0\\x+9=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=4\\x=-9\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2\\x=-9\end{matrix}\right.\)
Vậy \(x\) {-9; 2}
b; (\(x\) + 1).(\(x-1\)).(3 - 2\(x\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-1=0\\3-2x=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=1\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-1; 1; \(\dfrac{3}{2}\)}

a) x = 0 là nghiệm của P(x) nên:
P(0) = 0
2.0 + a - 1 = 0
a = 1
b) x = 1 là nghiệm của P(x) nên:
P(1) = 0
2.1 + a - 1 = 0
a + 1 = 0
a = -1
a) Do P(x) nhận `x=0` là nghiệm nên:
Thay `x=0` vào P(x) ta có:
\(2\cdot0+a-1=0\)
\(\Rightarrow a-1=0\)
\(\Rightarrow a=1\)
b) Do P(x) nhận `x=1` là nghiệm nên:
Thay `x=1` vào P(x) ta có:
\(2\cdot1+a-1=0\)
\(\Rightarrow2+a-1=0\)
\(\Rightarrow a+1=0\)
\(\Rightarrow a=-1\)

3x(12x – 4) – 9x(4x – 3) = 30
3x.12x – 3x.4 – (9x.4x – 9x.3) = 30
36x2 – 12x – 36x2 + 27x = 30
(36x2 – 36x2) + (27x – 12x) = 30
15x = 30
x = 2
Vậy x = 2.
Chúc bạn học tốt, tick cho tui nhoe

a: \(10x^2-7x+a⋮2x-3\)
=>\(10x^2-15x+8x-12+a+12⋮2x-3\)
=>a+12=0
=>a=-12
b: \(2x^2+ax-4⋮x+4\)
=>\(2x^2+8x+\left(a-8\right)x+4a-32-4a+28⋮x+4\)
=>-4a+28=0
=>a=7

a: A(x)+B(x)
\(=-3x^3+5x^2+4x+1+3x^3+6x^2-8x+9\)
\(=11x^2-4x+10\)
A(x)-B(x)
\(=-3x^3+5x^2+4x+1-3x^3-6x^2+8x-9\)
\(=-6x^3-x^2+12x-8\)
b: C(x)+D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}+4x^3-5x^2-3x-\dfrac{1}{4}\)
\(=3x^3+2x-1\)
C(x)-D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}-4x^3+5x^2+3x+\dfrac{1}{4}\)
\(=-5x^3+10x^2+8x-\dfrac{1}{2}\)
c: E(x)+F(x)
\(=3x^3+7x^2+5x-8+3x^3+7x^2-9x+1\)
\(=6x^3+14x^2-4x-7\)
E(x)-F(x)
\(=3x^3+7x^2+5x-8-3x^3-7x^2+9x-1\)
\(=14x-9\)
d: G(x)+H(x)
\(=5x^4-6x^3-3x^2-2x+8+x^4+3x^2-3x-5\)
\(=6x^4-6x^3-5x+3\)
G(x)-H(x)
\(=5x^4-6x^3-3x^2-2x+8-x^4-3x^2+3x+5\)
\(=4x^4-6x^3-6x^2+x+13\)
e: I(x)+J(x)
\(=5x^4-2x^3-6x^2+7x+6+2x^3+3x^2-7x-5\)
\(=5x^4-3x^2+1\)
I(x)-J(x)
\(=5x^4-2x^3-6x^2+7x+6-2x^3-3x^2+7x+5\)
\(=5x^4-4x^3-9x^2+14x+11\)
f: K(x)+L(x)
\(=4x^4+3x^3+5x^2-2x+6-4x^4-3x^3-4x^2+2x-9\)
\(=x^2-3\)
K(x)-L(x)
\(=4x^4+3x^3+5x^2-2x+6+4x^4+3x^3+4x^2-2x+9\)
\(=8x^4+6x^3+9x^2-4x+15\)
g: M(x)+N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19+6x^4-4x^3+3x^2+\dfrac{1}{2}x-20\)
\(=x^4-2x^2-39\)
M(x)-N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19-6x^4+4x^3-3x^2-\dfrac{1}{2}x+20\)
\(=-11x^4+8x^3-8x^2-x+1\)
h:
\(O\left(x\right)=x^5+x^3-4x-x^5+3x+7\)
\(=\left(x^5-x^5\right)+x^3+\left(-4x+3x\right)+7\)
\(=x^3-x+7\)
\(P\left(x\right)=3x^2-x^3+8x-3x^2-14\)
\(=-x^3+\left(3x^2-3x^2\right)+8x-14=-x^3+8x-14\)
O(x)+P(x)
\(=x^3-x+7-x^3+8x-14\)
\(=7x-7\)
O(x)-P(x)
\(=x^3-x+7+x^3-8x+14\)
\(=2x^3-9x+21\)

Lời giải:
Ta thấy:
$x^4\geq 0; x^2\geq 0$ với mọi $x$
$\Rightarrow Q(x)=x^4+3x^2+1\geq 1>0$ với mọi $x$
$\RIghtarrow Q(x)$ không có nghiệm với mọi $x$