cho góc xoy bé hơn 90 độ oz là tia phân giác. trên tia ox và oy lấy lần lượt a và b sao cho oa=ob. c là điểm trên tia oz sao cho oc>oa. tia ac cắt oy tại d, tia bc cắt ox tại f
a. c/m tam giác dac= tam giác obc
b. c/m tam giác dao= tam giác fbo
c. c/m oc vuông góc với ab
d. gọi m là trung điểm df. c/m d,c,m thẳng hàng

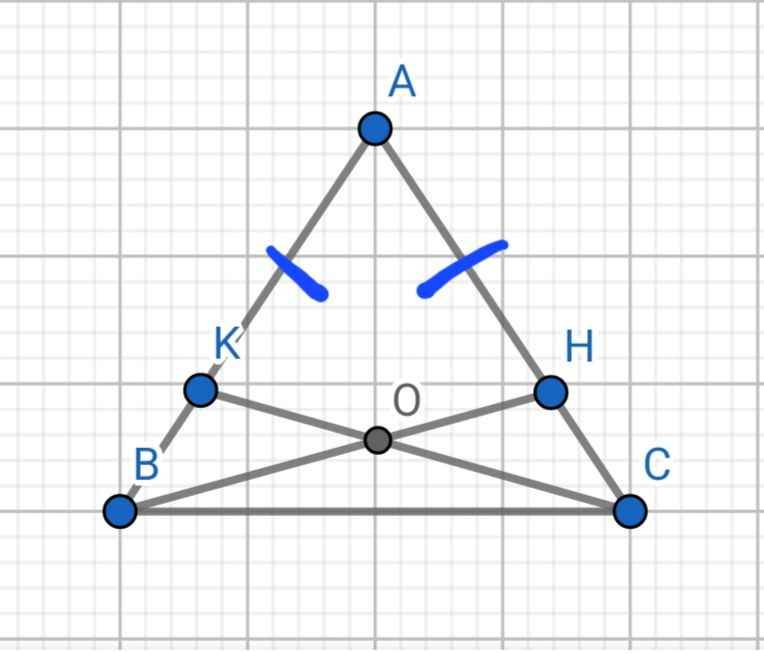
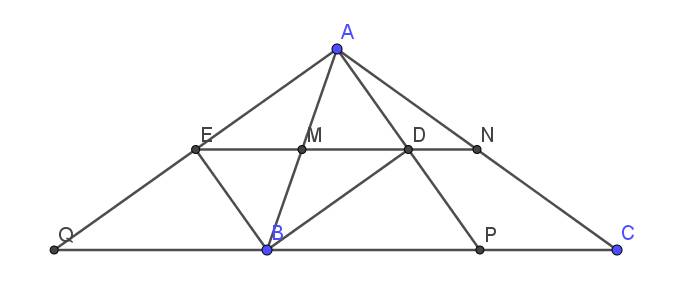
a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
b: TA có: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}\)
=>\(\widehat{OAD}=\widehat{OBF}\)
Xét ΔOAD và ΔOBF có
\(\widehat{OAD}=\widehat{OBF}\)
OA=OB
\(\widehat{AOD}\) chung
Do đó: ΔOAD=ΔOBF
c: Ta có: \(\widehat{OAC}+\widehat{CAF}=180^0\)(kề bù)
\(\widehat{OBC}+\widehat{CBD}=180^0\)(kề bù)
mà \(\widehat{OAC}=\widehat{OBC}\)
nên \(\widehat{CAF}=\widehat{CBD}\)
Ta có; ΔOAD=ΔOBF
=>\(\widehat{ODA}=\widehat{OFB}\) và OD=OF
Ta có: OA+AF=OF
OB+BD=OD
mà OA=OB và OF=OD
nên AF=BD
Xét ΔCAF và ΔCBD có
\(\widehat{CAF}=\widehat{CBD}\)
AF=BD
\(\widehat{CFA}=\widehat{CDB}\)
Do đó; ΔCAF=ΔCBD
=>CF=CD và CA=CB
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: CA=CB
=>C nằm trên đường trung trực của BA(2)
Từ (1),(2) suy ra OC là đường trung trực của BA
d: Ta có: OD=OF
=>O nằm trên đường trung trực của DF(3)
Ta có: CD=CF
=>C nằm trên đường trung trực của DF(4)
Ta có: MD=MF
=>M nằm trên đường trung trực của DF(5)
Từ (3),(4),(5) suy ra O,C,M thẳng hàng
chịu thôi em mới lớp 5