65,6 km² = 6560 ha

1 like nha bạn

65,6 km²=0,00656 ha

Mỗi quyển truyện tranh có giá là:

56000 : 8 = 7000 (đồng)

Số tiền của Dũng là:

56000 - 21000 = 35000 (đồng) 

Với 35000 đồng Dũng có thể mua được:
35000 : 7000 = 5 (quyển truyện tranh) 
ĐS: ...

Số tiền của Dũng là:

     56000-21000=35000 (đồng)

Giá tiền 1 quyển truyện trang là:

     56000:8=7000 (đồng)

Dũng mua được số quyển truyện tranh là:

     35000:7000=5 (quyển)

          Đáp số: 5 quyển truyện tranh

Bài 1:

a: BM=2MC

=>\(BM=\dfrac{2}{1+2}BC=\dfrac{2}{3}BC\)

Xét ΔABD có

BC là đường trung tuyến

\(BM=\dfrac{2}{3}BC\)

Do đó: M là trọng tâm của ΔABD

Xét ΔABD có

M là trọng tâm của ΔABD

N là trung điểm của BD

Do đó: A,M,N thẳng hàng

b: Vì M là trọng tâm của ΔABD 

nên DM đi qua trung điểm của AB

Bài 2:

a: G là trung điểm của BK

=>\(BG=GK=\dfrac{BK}{2}\)

Ta có: BG+GM=BM

=>\(GM+\dfrac{2}{3}BM=BM\)

=>\(GM=\dfrac{1}{3}BM\)

=>BG=2GM

=>GK=2GM

=>M là trung điểm của GK

=>MG=MK

Xét ΔKGC có

GE,CM là các đường trung tuyến

GE cắt CM tại I

Do đó: I là trọng tâm của ΔKGC

b: Xét ΔKGC có

I là trọng tâm

CM là đường trung tuyến

Do đó: \(CI=\dfrac{2}{3}CM=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}AC\)

0,6% nãy LS theo tháng hay năm em?

ra 240000000đ

\(8A+1=\left(3^{51}\right)^2\)

⇒ 8A + 1 là một số chính phương 

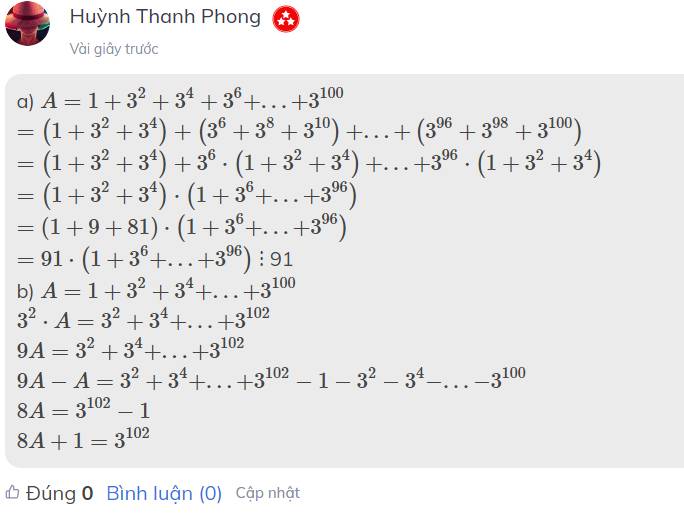
a) \(A=1+3^2+3^4+3^6+...+3^{100}\)

\(=\left(1+3^2+3^4\right)+\left(3^6+3^8+3^{10}\right)+...+\left(3^{96}+3^{98}+3^{100}\right)\)

\(=\left(1+3^2+3^4\right)+3^6\cdot\left(1+3^2+3^4\right)+...+3^{96}\cdot\left(1+3^2+3^4\right)\)

\(=\left(1+3^2+3^4\right)\cdot\left(1+3^6+...+3^{96}\right)\)

\(=\left(1+9+81\right)\cdot\left(1+3^6+...+3^{96}\right)\)

\(=91\cdot\left(1+3^6+...+3^{96}\right)\) ⋮ 91 

b) \(A=1+3^2+3^4+...+3^{100}\)

\(3^2\cdot A=3^2+3^4+...+3^{102}\)

\(9A=3^2+3^4+...+3^{102}\)

\(9A-A=3^2+3^4+...+3^{102}-1-3^2-3^4-...-3^{100}\)

\(8A=3^{102}-1\)

\(8A+1=3^{102}\) 

Số học sinh không tham gia là:

`30-12=18` (học sinh)

Số học sinh không tham gia chiếm số phần trăm là:

\(18:30\times100\%=60\%\)

ĐS: 605

Số học sinh không tham gia là:

$30-12=18$ (học sinh)

Số học sinh không tham gia chiếm số phần trăm là:

$18:30\times 100\%=60\%$

ĐS: 605

a: Xét ΔABC vuông tại A và ΔAEC vuông tại A có

AB=AE

AC chung

Do đó: ΔABC=ΔAEC

b: Xét ΔCBE có

BH,CA là các đường trung tuyến

BH cắt CA tại M

Do đó: M là trọng tâm của ΔCBE

c: Xét ΔBCE có

A là trung điểm của BE

AK//CE

Do đó: K là trung điểm của CB

Xét ΔBCE có

M là trọng tâm 

K là trung điểm của BC

Do đó: E,M,K thẳng hàng

a: ΔDEF vuông tại D

=>\(\widehat{DEF}+\widehat{DFE}=90^0\)

=>\(\widehat{DFE}+30^0=90^0\)

=>\(\widehat{DFE}=60^0\)

Xét ΔDEF có \(\widehat{DEF}< \widehat{DFE}< \widehat{EDF}\)

mà DF,DE,EF lần lượt là cạnh đối diện của các góc DEF,DFE,EDF

nên DF<DE<EF

b: Xét ΔFDG vuông tại D và ΔFKG vuông tại K có

FG chung

\(\widehat{DFG}=\widehat{KFG}\)

Do đó: ΔFDG=ΔFKG

c: Ta có: ΔFDG=ΔFKG

=>GD=GK

mà GK<GE(ΔGKE vuông tại K)

nên GD<GE

d: Ta có: ΔFDG=ΔFKG

=>FD=FK

Xét ΔFKM vuông tại K và ΔFDE vuông tại D có

FK=FD

\(\widehat{KFM}\) chung

Do đó: ΔFKM=ΔFDE

=>FM=FE

Xét ΔFME có FM=FE và \(\widehat{MFE}=60^0\)

nên ΔFME đều

\(P=\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2023}\)

\(=\dfrac{1}{2\cdot\dfrac{3}{2}}+\dfrac{1}{3\cdot\dfrac{4}{2}}+...+\dfrac{1}{2023\cdot\dfrac{2024}{2}}\)

\(=\dfrac{2}{2\cdot3}+\dfrac{2}{3\cdot4}+...+\dfrac{2}{2023\cdot2024}\)

\(=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\right)\)

\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\right)\)

\(=2\left(\dfrac{1}{2}-\dfrac{1}{2024}\right)=1-\dfrac{1}{1012}=\dfrac{1011}{1012}\)

p=1/3(1-1/2 mũ 2025)