
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A tích của hai số là 276 nếu thêm vào số thứ nhất 19 đơn vị thì tích của hai số là 713 tìm hai số đó

Gọi hai thừa số lần lượt là a;b.
a.b=276
(a+19).b=713
a.b+b.19=713
b.19=713-276
b.19=437
b=437:19
b=23
a=276:23
a=12
Vậy hai số đó là 12 và 23

\(\Leftrightarrow x^2+2y^2+3xy-4x-5y+3=4\)
\(\Leftrightarrow\left(x^2+2xy-3x\right)+\left(xy+2y^2-3y\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow x\left(x+2y-3\right)+y\left(x+2y-3\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow\left(x+2y-3\right)\left(x+y-1\right)=4\)
Ta có bảng:
| x+2y-3 | -4 | -2 | -1 | 1 | 2 | 4 |
| x+y-1 | -1 | -2 | -4 | 4 | 2 | 1 |
| x | 1 | -3 | -8 | 6 | 1 | -3 |
| y | -1 | 2 | 5 | -1 | 2 | 5 |
Vậy \(\left(x;y\right)=\left(1;-1\right);\left(-3;2\right);\left(-8;5\right);\left(6;-1\right);\left(1;2\right);\left(-3;5\right)\)

Bạn xem lại đề, quy luật của các số hạng trong tổng có vẻ chưa rõ ràng lắm.

1)
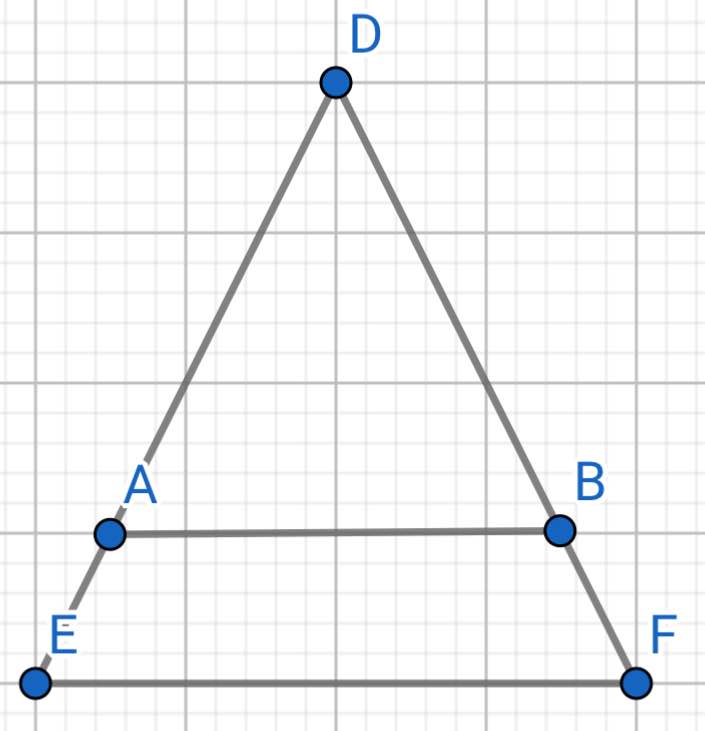
a) Do tam giác DEF cân tại D (gt)
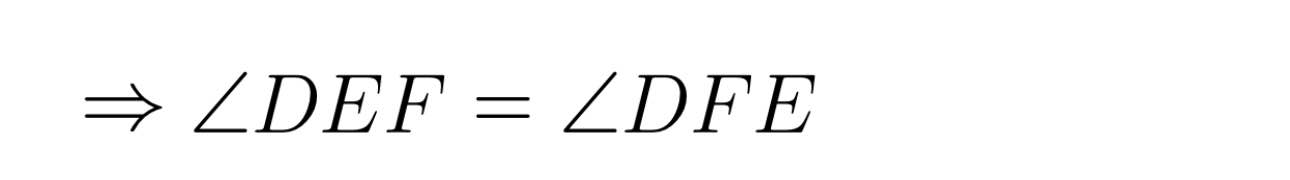
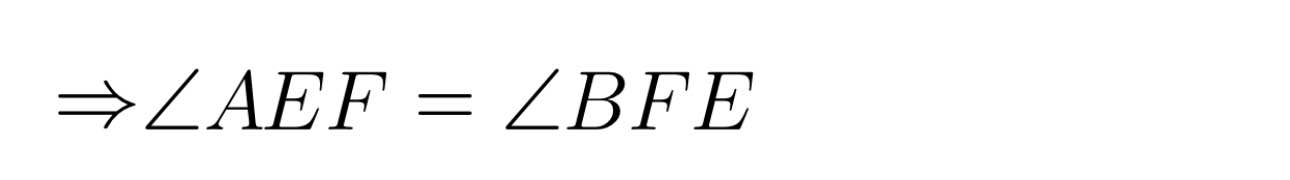
Tam giác DAB có:
DA = DB (gt)
=> Tam giác DAB cân tại D
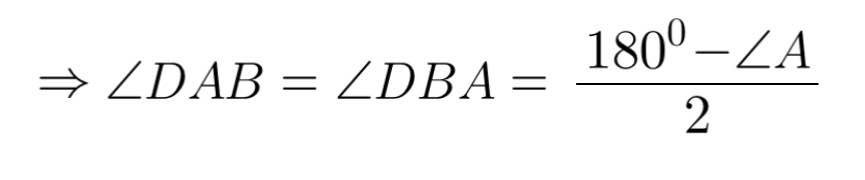
Do tam giác DEF cân tại D (gt)
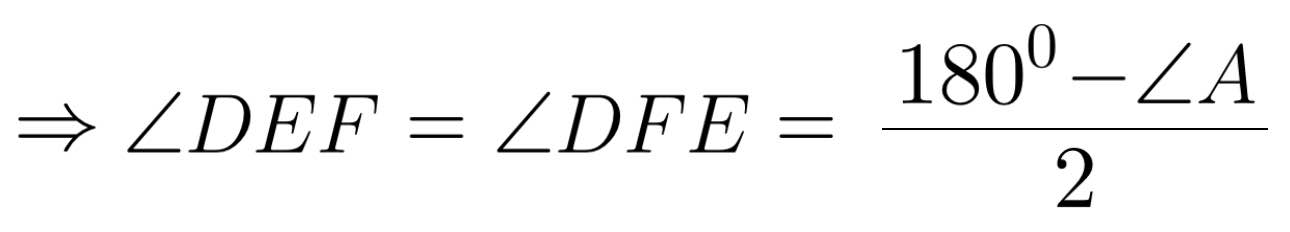
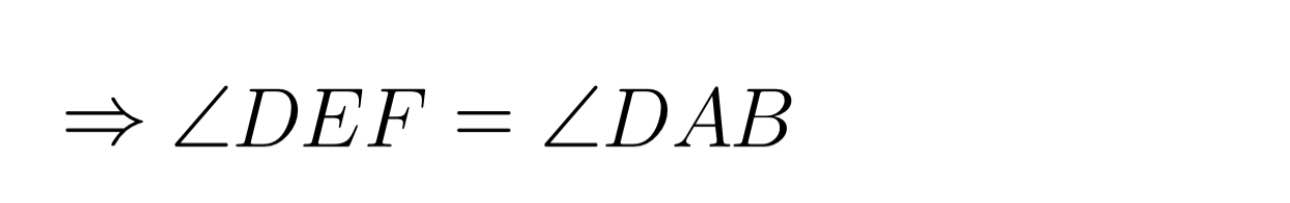
Mà góc DEF và góc DAB đồng vị

=> EABF là hình thang
Mà:
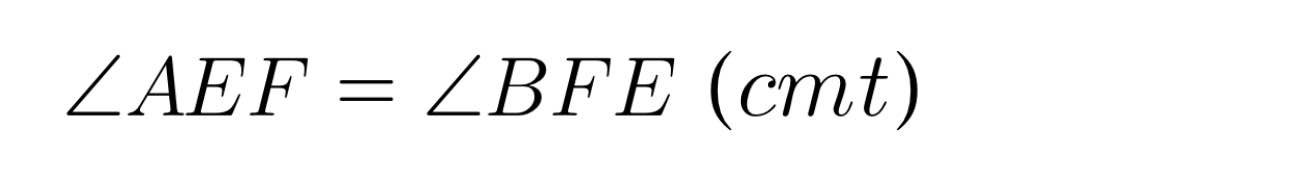
=> EABF là hình thang cân
b) Do tam giác DEF cân tại D (gt)
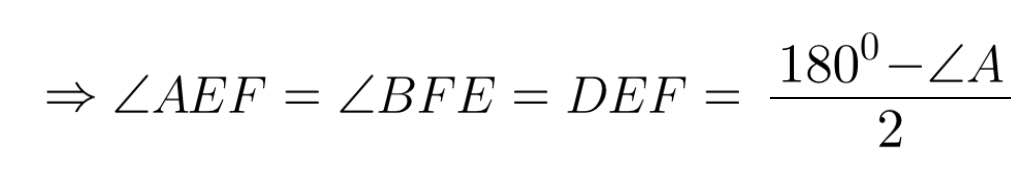
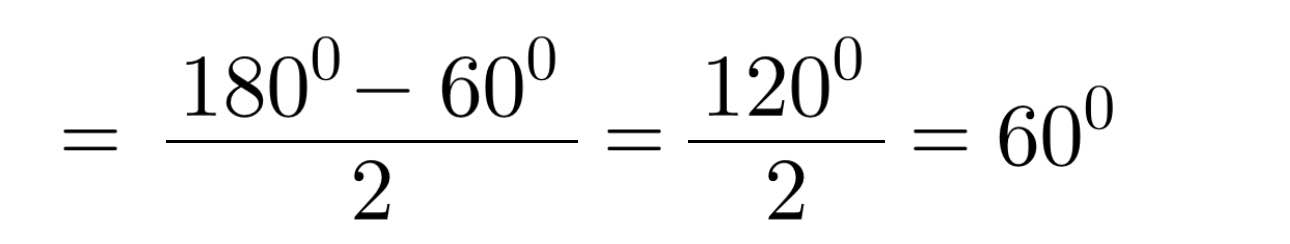
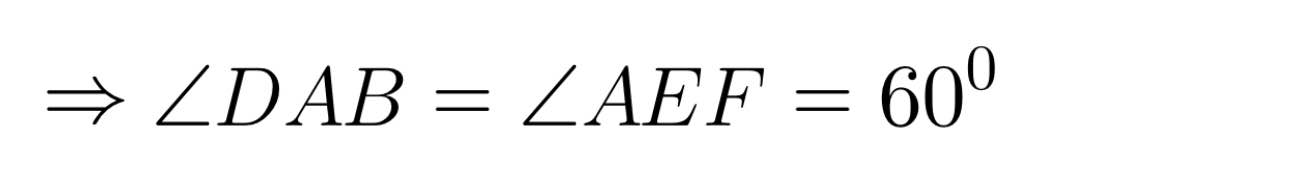
Ta có:
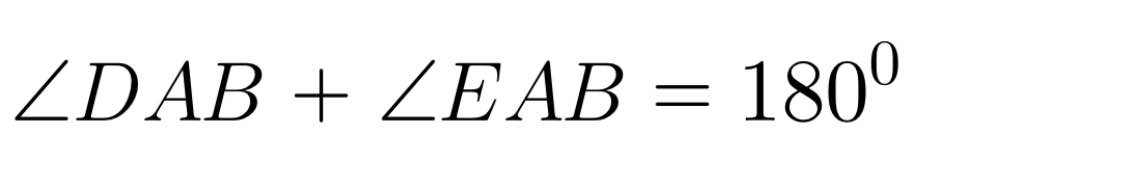
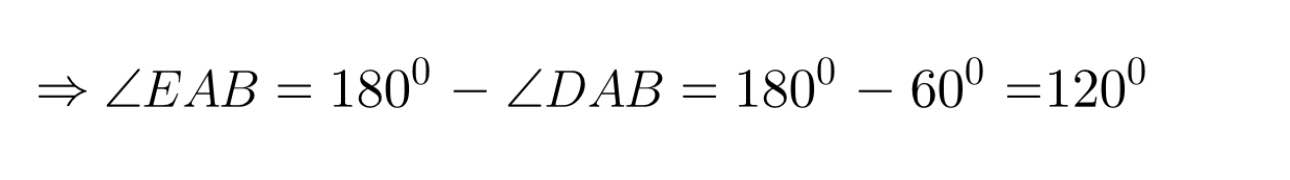

Bài 3
Tam giác ABD có:
AB = AD (gt)
=> Tam giác ABD cân tại A
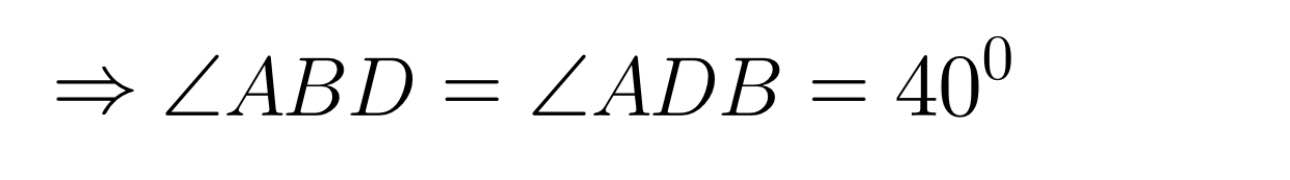
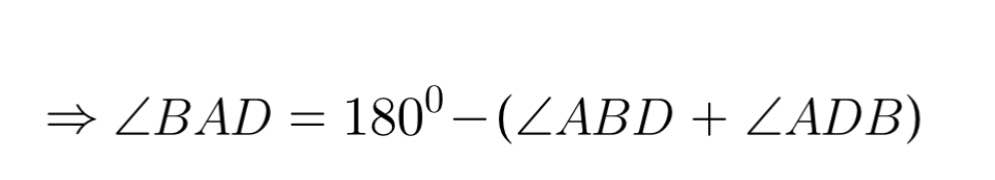
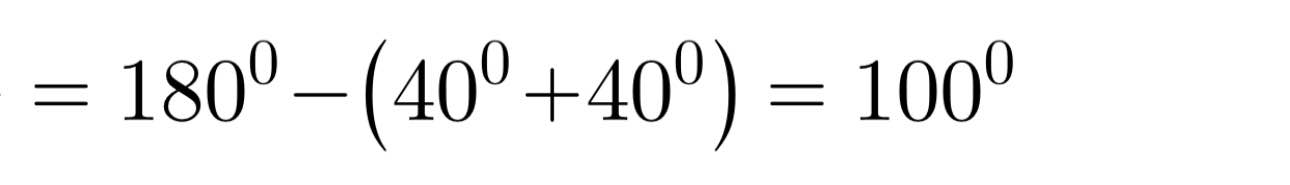
Ta có:
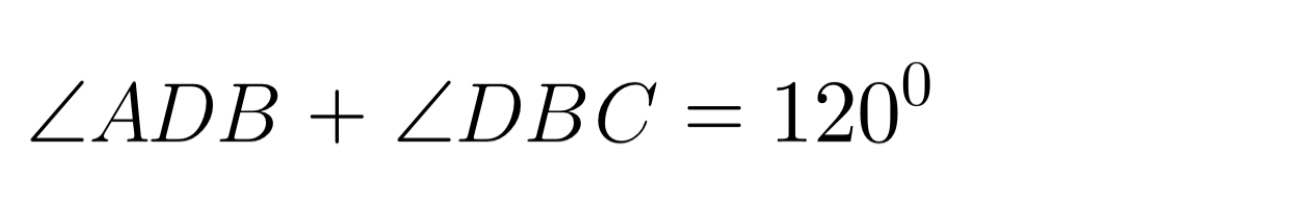
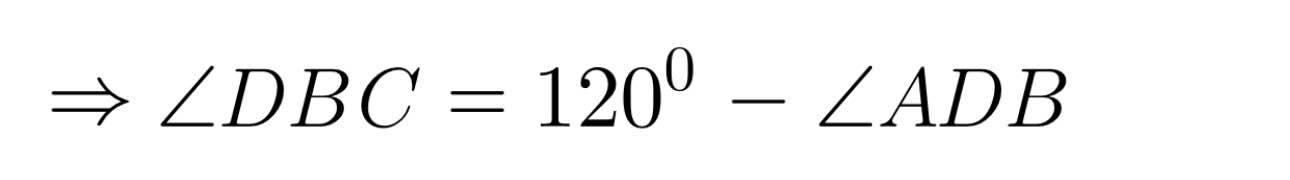
= 120⁰ − 40⁰
= 80⁰
Tam giác BCD có:
CB = CD (gt)
=> Tam giác BCD cân tại C
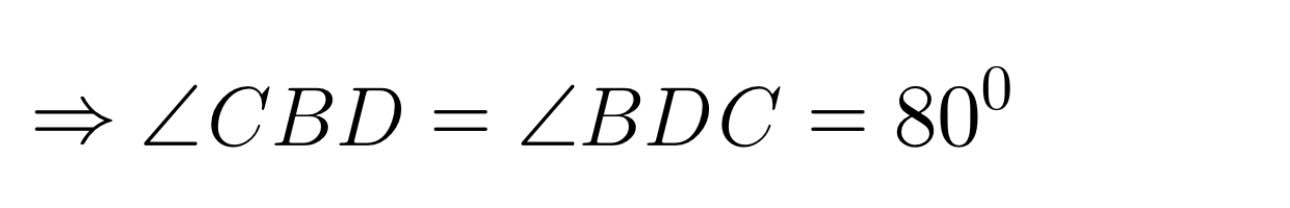
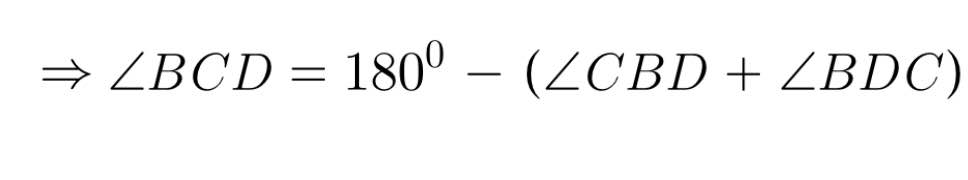
= 180⁰ − (80⁰ + 80⁰) = 20⁰
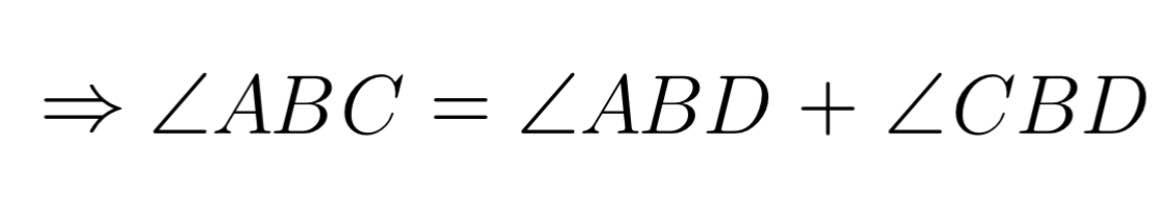
= 40⁰ + 40⁰
= 80⁰

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{13^2-5^2}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(cosBAH=\dfrac{AH}{AB}=\dfrac{60}{13}:5=\dfrac{12}{13}\)
nên \(\widehat{BAH}\simeq23^0\)

Số tấn hàng mỗi chuyến xe chở được:
6 : 3 = 2 (tấn)
Trong 6 chuyến xe tải chở được số tấn hàng là:
2 × 6= 12 (tấn)

Đáp án: Phòng 3
Giải thích: Sư tử nhịn đói trong ba năm thì sư tử đã chết, vậy nên căn phòng đó an toàn.
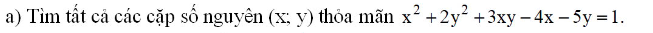

\(D=\dfrac{2^2-1}{2^2}+\dfrac{3^2-1}{3^2}+...+\dfrac{2025^2-1}{2025^2}\)
\(=\left(\dfrac{2^2}{2^2}+\dfrac{3^2}{3^2}+...+\dfrac{2025^2}{2025^2}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=\left(1+1+...+1\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=2024-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+....+\dfrac{1}{2025^2}\right)\)
Đặt \(E=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\)
Do \(E>0\Rightarrow D< 2024\) (1)
Lại có:
\(E< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2024.2025}\)
\(E< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2024}-\dfrac{1}{2025}\)
\(E< 1-\dfrac{1}{2025}< 1\)
\(\Rightarrow D-E>2024-1=2023\) (2)
(1);(2) \(\Rightarrow2023< D< 2024\)
\(\Rightarrow D\) nằm giữa 2 số tự nhiên liên tiếp nên D ko thể là số tự nhiên