số cách chọn là 

12C4 - 5C1.4C1.3C2 - 5C1.4C2.3C1- 5C2.4C1.3C1

a: Tổng vận tốc của hai xe là 54+36=90(km/h)

1h48p=1,8(giờ)

Độ dài quãng đường AB là:

90x1,8=162(km)

b: Thời gian ô tô đi từ B đến A là:

162:54=3(giờ)

Sau 3 giờ thì xe máy còn cách B:

162-3x36=54(km)

\(\dfrac{7}{-3}\) là phân số.

Trong các số trên, \(\dfrac{7}{-3}\) là phân số.

\(A=1+\dfrac{1}{1+2}+...+\dfrac{1}{1+2+...+8}\)

\(=\dfrac{2}{2}+\dfrac{1}{2\cdot\dfrac{3}{2}}+...+\dfrac{1}{8\cdot\dfrac{9}{2}}\)

\(=\dfrac{2}{1\cdot2}+\dfrac{2}{2\cdot3}+...+\dfrac{2}{8\cdot9}\)

\(=2\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\right)\)

\(=2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)\)

\(=2\left(1-\dfrac{1}{9}\right)=2\cdot\dfrac{8}{9}=\dfrac{16}{9}\)

a: Xét ΔBAM vuông tại A và ΔBKM vuông tại K có

BM chung

\(\widehat{ABM}=\widehat{KBM}\)

Do đó: ΔBAM=ΔBKM

=>BA=BK

=>ΔBAK cân tại B

b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)

\(\widehat{DAK}+\widehat{BKA}=90^0\)(ΔDAK vuông tại D)

mà \(\widehat{BAK}=\widehat{BKA}\)(ΔBAK cân tại B)

nên \(\widehat{CAK}=\widehat{DAK}\)

=>AK là phân giác của góc DAC

c: Xét ΔABC vuông tại A có AD là đường cao

nên \(AD\cdot BC=AB\cdot AC\)

\(\left(AB+AC\right)^2-\left(BC+AD\right)^2\)

\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-2\cdot BC\cdot AD-AD^2\)

\(=BC^2+2\cdot BC\cdot AD-BC^2-2\cdot BC\cdot AD-AD^2\)

\(=-AD^2< 0\)

=>\(\left(AB+AC\right)^2< \left(BC+AD\right)^2\)

=>AB+AC<BC+AD

Ta thực hiện theo các bước sau:

Bước 1. Xác định ba điểm A, B, C nằm trên rìa mảnh gỗ .

Bước 2. Xác định ba đường trung trực của tam giác ABC.

Bước 3. Xác định giao điểm của ba đường trung trực của tam giác ABC.

Điểm đó là tâm của mảnh gỗ

Cái  thì tui chịu

Sửa đề:

ABC cân tại A có BH và CK là hai đường cao

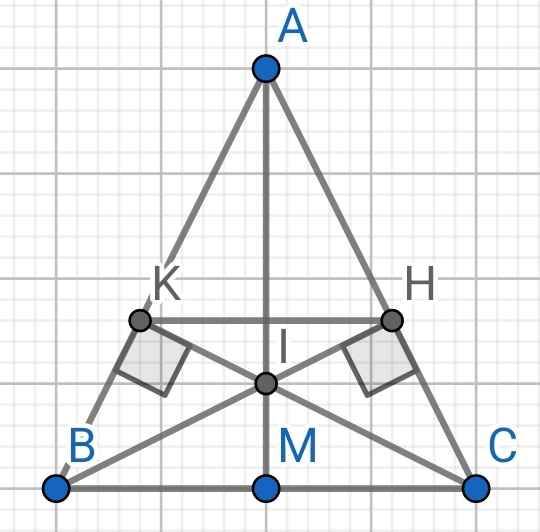
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AKC có:

AB = AC (cmt)

∠A chung

⇒ ∆AHB = ∆AKC (cạnh huyền - góc nhọn)

⇒ AH = AK (hai cạnh tương ứng)

⇒ ∆AKH cân tại A

b) ∆ABC cân tại A (gt)

BH và CK là hai đường cao cắt nhau tại I (gt)

⇒ AI là đường cao thứ ba

⇒ AI ⊥ BC

⇒ IM ⊥ BC

Do ∆ABC cân tại A có

AI là đường cao (cmt)

⇒ AM là đường cao

⇒ AM cũng là đường trung tuyến

⇒ M là trung điểm của BC

⇒ MB = MC

Xét hai tam giác vuông: ∆IBM và ∆ICM có:

IM là cạnh chung

MB = MC (cmt)

⇒ ∆IBM = ∆ICM (hai cạnh góc vuông)

⇒ ∠BIM = ∠CIM (hai góc tương ứng)

⇒ IM là tia phân giác của ∠BIC

c) Xét hai tam giác vuông: ∆AHI và ∆AKI có:

AI là cạnh chung

AH = AK (cmt)

⇒ ∆AHI = ∆AKI (cạnh huyền - cạnh góc vuông)

⇒ IH = IK (hai cạnh tương ứng)

⇒ I nằm trên đường trung trực của HK (1)

Do AH = AK (cmt)

⇒ A nằm trên đường trung trực của HK (2)

Từ (1) và (2) ⇒ AI là đường trung trực của HK

⇒ AI ⊥ HK

Lại có:

AI ⊥ BC (cmt)

⇒ HK // BC