Cho ba số thực a,b,c khác 0 thoả mãn a(1/b+1/c)+ b(1/c+1/a)+ c(1/a+1/c)= -2. Chứng minh rằng (a+b)(b+c)(c+a)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\dfrac{\sqrt[]{6}+\sqrt[]{14}}{2\sqrt[]{3}+\sqrt[]{28}}=\dfrac{\sqrt[]{2}\left(\sqrt[]{3}+\sqrt[]{7}\right)}{2\left(\sqrt[]{3}+\sqrt[]{7}\right)}=\dfrac{\sqrt[]{2}}{2}\)
2) \(\dfrac{\sqrt[]{5}-\sqrt[]{10}}{\sqrt[]{3}-\sqrt[]{6}}=\dfrac{\sqrt[]{5}\left(1-\sqrt[]{2}\right)}{\sqrt[]{3}\left(1-\sqrt[]{2}\right)}=\sqrt[]{\dfrac{5}{3}}\)
3) \(...=\dfrac{4\sqrt[]{2}-2\sqrt[]{3}}{3\sqrt[]{2}-4\sqrt[]{3}}-\dfrac{\sqrt[]{5}+\sqrt[]{27}}{\sqrt[]{6}\left(\sqrt[]{5}+\sqrt[]{27}\right)}\)
\(=\dfrac{2\left(2\sqrt[]{2}-\sqrt[]{3}\right)}{3\sqrt[]{2}-4\sqrt[]{3}}-\dfrac{1}{\sqrt[]{6}}\)
\(=\dfrac{2\sqrt[]{6}\left(2\sqrt[]{2}-\sqrt[]{3}\right)-\left(3\sqrt[]{2}-4\sqrt[]{3}\right)}{\sqrt[]{6}\left(3\sqrt[]{2}-4\sqrt[]{3}\right)}\)
\(=\dfrac{8\sqrt[]{3}-6\sqrt[]{2}-3\sqrt[]{2}+4\sqrt[]{3}}{6\sqrt[]{3}-12\sqrt[]{3}}\)
\(=\dfrac{12\sqrt[]{3}-9\sqrt[]{2}}{-6\sqrt[]{3}}=-2+\sqrt[]{\dfrac{3}{2}}\)
Bài 4 bạn tự làm nhé

\(17-\dfrac{12}{\sqrt[]{2}}=17-6\sqrt[]{2}=18-6\sqrt[]{2}+1-2\)
\(=\left(\sqrt[]{18}-1\right)^2-2=\left(3\sqrt[]{2}-1\right)^2-2\)

Bài 1 :
\(...\Rightarrow A=\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+2\right)+\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}-2\right)}{\left(\sqrt[]{x}-2\right)\left(\sqrt[]{x}+2\right)}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{x+2\sqrt[]{x}+x-3\sqrt[]{x}+2}{x-4}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-\sqrt[]{x}+2-\sqrt[]{x}+10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-2\sqrt[]{x}+12}{x-4}=\dfrac{2\left(x-\sqrt[]{x}+6\right)}{x-4}\)

Ta có:
\(P=\left(2+\sqrt{2}\right)^7+\left(2-\sqrt{2}\right)^7\)
\(P=2^7+7.2^6\sqrt{2}+21.2^5\left(\sqrt{2}\right)^2+...+7.2\left(\sqrt{2}\right)^6+\left(\sqrt{2}\right)^7\)\(+2^7-7.2^6\sqrt{2}+21.2^5\left(\sqrt{2}\right)^2-...+7.2\left(\sqrt{2}\right)^6-\left(\sqrt{2}\right)^7\)
\(P=2.2^7+2.21.2^5.\left(\sqrt{2}\right)^2+2.35.2^3.\left(\sqrt{2}\right)^4+2.7.2.\left(\sqrt{2}\right)^6\)
\(P=2^8+21.2^7+35.2^6+7.2^5\)
\(P=5408\)
\(\Rightarrow\left(2+\sqrt{2}\right)^7=5408-\left(2-\sqrt{2}\right)^7\)
Do \(0< \left(2-\sqrt{2}\right)^7< 1\) nên suy ra \(5047< \left(2+\sqrt{2}\right)^7< 5048\)
Vậy số nguyên lớn nhất không vượt quá \(\left(2+\sqrt{2}\right)^7\) là 5047.
(Sau này ta kí hiệu như thế này cho gọn.)

ĐKXĐ : \(x\inℝ\)
Ta có : x2 + 4x + 7 = (x + 4)\(\sqrt{x^2+7}\)
\(\Leftrightarrow x^2+7+4x=x\sqrt{x^2+7}+4\sqrt{x^2+7}\) (*)
Đặt \(\sqrt{x^2+7}=a>0\)
Có (*) \(\Leftrightarrow a^2+4x=ax+4a\)
\(\Leftrightarrow\left(a-x\right).\left(a-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=x\\a=4\end{matrix}\right.\)
Với a = x \(\Leftrightarrow\sqrt{x^2+7}=x\Leftrightarrow\left\{{}\begin{matrix}x^2+7=x^2\\x>0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Với a = 4 \(\Leftrightarrow\sqrt{x^2+7}=4\Leftrightarrow x^2+7=16\Leftrightarrow x=\pm3\)
Thử lại thấy thỏa mãn
Tập nghiệm \(S=\left\{\pm3\right\}\)
\(x^2+4x+7=\left(x+4\right)\sqrt[]{x^2+7}\)
\(\Leftrightarrow x^2+7+4x=\left(x+4\right)\sqrt[]{x^2+7}\left(1\right)\)
Đặt \(t=\sqrt[]{x^2+7}\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2+4x=\left(x+4\right).t\)
\(\Leftrightarrow t^2-\left(x+4\right).t+4x=0\)
\(\Leftrightarrow t^2-tx-4.t+4x=0\)
\(\Leftrightarrow t\left(t-x\right)-4\left(t-x\right)=0\)
\(\Leftrightarrow\left(t-x\right)\left(t-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-x=0\\t-4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}t=x\\t=4\end{matrix}\right.\)
- Với \(t=x\Leftrightarrow\sqrt[]{x^2+7}=x\Leftrightarrow x^2+7=x^2\Leftrightarrow0.x^7=7\left(loại\right)\)
- Với \(t=4\Leftrightarrow\sqrt[]{x^2+7}=4\Leftrightarrow x^2+7=16\Leftrightarrow x^2=9\Leftrightarrow x=\pm3\)
Vậy nghiệm phương trình là \(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

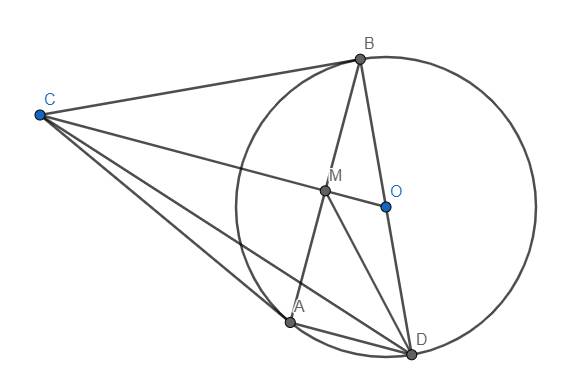
Dễ dàng chứng minh \(OM.OC=OA^2=OD^2\). \(\Rightarrow\Delta OMD~\Delta ODC\left(c.g.c\right)\) \(\Rightarrow\widehat{ODM}=\widehat{OCD}\)
Mà \(\widehat{OCD}=\widehat{ADC}\) (do OC//AD (\(\perp AB\))) nên suy ra \(\widehat{ADC}=\widehat{BDM}\) (đpcm)

Cách 1:
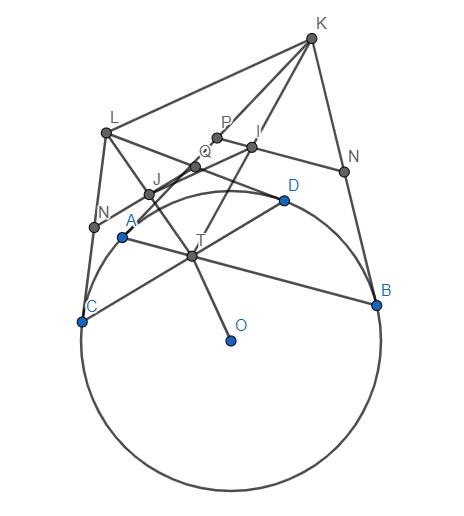
Gọi I, J, M, N, P, Q lần lượt là trung điểm của TK, TL, KB, LC, KA, LD.
Ta có \(MB^2=MK^2\) \(\Rightarrow P_{M/\left(O\right)}=P_{M/\left(K;0\right)}\) \(\Rightarrow\) M nằm trên trục đẳng phương của (O) và (K;0). Tương tự, ta có P nằm trên trục đẳng phương của (O) và (K;0) nên MP là trục đẳng phương của (O) và (K;0)
Hơn nữa, dễ thấy \(I\in MP\) nên \(P_{I/\left(O\right)}=P_{I/\left(K;0\right)}\Rightarrow P_{I/\left(O\right)}=IK^2\)
Mà \(IK=IT\Rightarrow P_{I/\left(O\right)}=IT^2=P_{I/\left(T;0\right)}\)
Hoàn toàn tương tự, ta chứng minh được \(P_{J/\left(O\right)}=P_{J/\left(T;0\right)}\), suy ra IJ là trục đẳng phương của (O) và (T;0) \(\Rightarrow IJ\perp OT\)
Mà IJ//LK (IJ là đường trung bình của tam giác TLK) \(\Rightarrow OT\perp KL\) (đpcm)

A B O C M D E F K
Dựng tiếp tuyến với đường tròn tại B, gọi K là giao của tiếp tuyến với đường tròn tại M với tiếp tuyến với đường tròn tại B
Ta có
\(AF\perp AB;OD\perp AB;BK\perp AB\) => AF//OD//BK
\(\Rightarrow\dfrac{DE}{OA}=\dfrac{DK}{OB}\) (Talet)
Mà OA=OB
=> DE=DK (1)
Xét tg ABF có
OD//AF => \(\dfrac{DF}{OA}=\dfrac{DB}{OB}\) (Talet trong tg)
Mà OA=OB => DF=DB (2)
\(\widehat{EDF}=\widehat{KDB}\) (góc đối đỉnh)
Từ (1) (2) (3) => tg EDF = tg KDB (c.g.c)
=> EF=KB
Mà KB=KM (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> EF=KM
Ta có
EA=EM (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
\(\Rightarrow EA.EF=EM.KM\)
Xét tg vuông EAO và tg vuông EMO có
EO chung
EA=EM (cmt)
=> tg EAO = tg EMO (Hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{EOA}=\widehat{EOM}\) (4)
C/m tương tự ta cũng có tg KMO = tg KBO \(\Rightarrow\widehat{KOB}=\widehat{KOM}\) (5)
Mà \(\widehat{EOA}+\widehat{EOM}+\widehat{KOB}+\widehat{KOM}=180^o\) (6)
Từ (4) (5) (6) \(\Rightarrow\widehat{EOM}+\widehat{KOM}=\widehat{KOE}=90^o\)
=> tg KOE là tg vuông tại O
Ta có \(OM\perp KE\) (KE là tiếp tuyến với đường tròn tại M)
Xét tg vuông KOE có
\(OM^2=KM.EM\) (Trong tg vuông bình phương đường cao từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow KM.EM=EF.EA=OM^2\) không đổi

B C P A H I O K x
Gọi I là giao của CP với AH; K là giao của CA với BP
\(sđ\widehat{CAx}=\dfrac{1}{2}sđcungAC\) (góc giữa tiếp tuyến và dây cung) (1)
\(sđ\widehat{BKC}=\dfrac{1}{2}\left(sđcungBC-sđcungAB\right)\) (góc có đỉnh ở ngoài hình tròn)
Ta có
\(sđcungBC=sđcungBAC\)
\(\Rightarrow sđcungBC-sđcungAB=sđcungBAC-sđcungAB=sđcungAC\)
\(\Rightarrow sđ\widehat{BKC}=\dfrac{1}{2}sđcungAC\) (2)
\(\widehat{CAx}=\widehat{KAP}\) (góc đối đỉnh) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{KAP}=\widehat{BKC}\) => tg APK cân tại P
=> PA=PK
Mà PA=PB (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> PK=PB
Ta có
\(BK\perp BC;AH\perp BC\) => AH//BK
Xét tg BCK có
\(\dfrac{IA}{PK}=\dfrac{IH}{PB}\) mà PK=PB (cmt) => IA=IH => I là trung điểm của AH
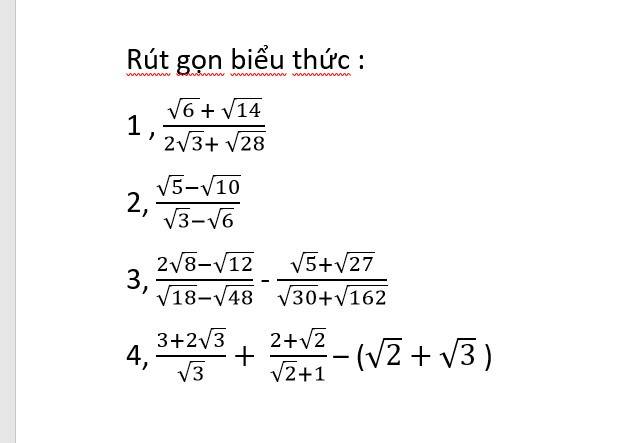

Giúp vs mn ơi
Cái cuối là c(1/a+1/b) nha mn