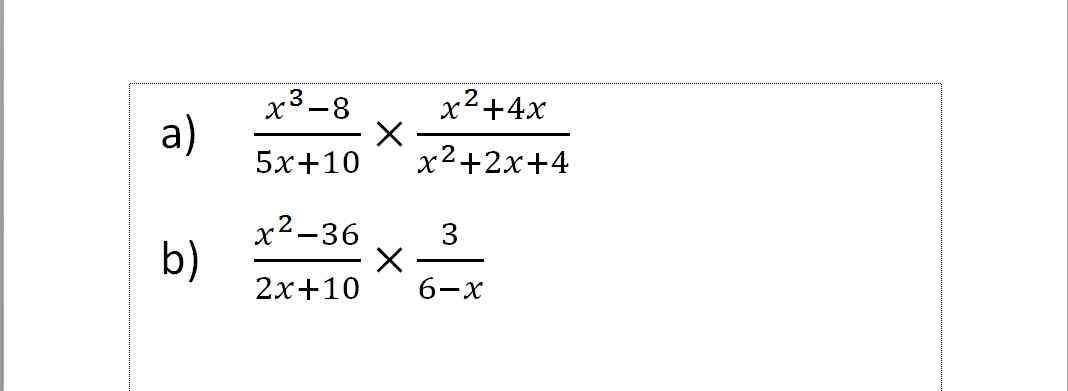a)

\(\dfrac{x^3-8}{5x+10}.\dfrac{x^2+4x}{x^2+2x+4}=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{5\left(x+2\right)}.\dfrac{x\left(x+4\right)}{x^2+2x+4}\\ =\dfrac{\left(x-2\right).\left(x^2+4x\right)}{5x+10}\\ =\dfrac{x^3+4x^2-2x^2-8x}{5x+10}\\ =\dfrac{x^3+2x^2-8x}{5x+10}\)

b)

\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2x+10}.-\dfrac{3}{x-6}\\ =\dfrac{-3\left(x+6\right)}{2x+10}\\ =\dfrac{-3x-18}{2x+10}\)

Lời giải:
a.

\(P=\left[\frac{\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}-\frac{3}{\sqrt{x}(\sqrt{x}-2)}\right]:\frac{\sqrt{x}-3}{(\sqrt{x}-2)^2}\\ =\frac{\sqrt{x}-3}{\sqrt{x}(\sqrt{x}-2)}.\frac{(\sqrt{x}-2)^2}{\sqrt{x}-3}\\ =\frac{\sqrt{x}-2}{\sqrt{x}}\)

b.

\(P=\frac{\sqrt{x}-2}{\sqrt{x}}=1-\frac{2}{\sqrt{x}}< 1\)

giải bài toán: cho tam giác MNP, NTlà phân giác của góc N biết MN=4cm, NT=10cm, MP=8cm:TínhTM, TP? 

Ta có \(\dfrac{1}{a^3\left(b+c\right)}=\dfrac{1}{\dfrac{1}{b^3c^3}\left(b+c\right)}=\dfrac{b^2c^2}{\dfrac{1}{b}+\dfrac{1}{c}}\)

Tương tự \(\Rightarrow VT=\dfrac{b^2c^2}{\dfrac{1}{b}+\dfrac{1}{c}}+\dfrac{c^2a^2}{\dfrac{1}{c}+\dfrac{1}{a}}+\dfrac{a^2b^2}{\dfrac{1}{a}+\dfrac{1}{b}}\)

\(\ge\dfrac{\left(ab+bc+ca\right)^2}{2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)}\) (BĐT B.C.S)

\(=\dfrac{\left(ab+bc+ca\right)^2}{2\left(\dfrac{ab+bc+ca}{abc}\right)}\)

\(=\dfrac{ab+bc+ca}{2}\) (do \(abc=1\))

\(\ge\dfrac{3\sqrt[3]{abbcca}}{2}\)

\(=\dfrac{3\left(\sqrt[3]{abc}\right)^2}{2}=\dfrac{3}{2}\) (do \(abc=1\))

ĐTXR \(\Leftrightarrow a=b=c=1\)

Ta có:

\(a^3+b^3=3ab-1\)

\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2\right)=3ab-1\)

\(\Leftrightarrow\left(a+b\right)\left(a^2+2ab+b^2-3ab\right)=3ab-1\)

\(\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)=3ab-1\)

\(\Leftrightarrow\left(a+b\right)^3+1-3ab\left(a+b\right)-3ab=0\)

\(\Leftrightarrow\left(a+b+1\right)\left[a^2+2ab+b^2-a-b+1\right]-3ab\left(a+b+1\right)=0\)

\(\Leftrightarrow\left(a+b+1\right)\left(a^2+2ab+b^2-a-b+1-3ab\right)=0\)

\(\Leftrightarrow\left(a+b+1\right)\left(a^2-ab+b^2-a-b+1\right)=0\)

\(\Leftrightarrow\left(a+b+1\right)\left(2a^2+2b^2-2ab-2a-2b+2\right)=0\)

\(\Leftrightarrow\left(a+b+1\right)\left(a^2-2a+1+b^2-2b+1+a^2-2ab+b^2\right)=0\)

\(\Leftrightarrow\left(a+b+1\right)\left[\left(a-1\right)^2+\left(b-1\right)^2+\left(a-b^2\right)\right]=0\)

.......

Mình nghĩ đề a, b là 2 số dương nha, nếu a,b là 2 số dương thì mình loại được trường hợp a+b+1=0 nhé

tra loi đi