a=(x^3-3x/x^2-9 -1):(9-x^2/(x+3)(x-2)+x+3/x-2-x+2/x+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn xem lại nhé. Đa thức đã cho không phân tích được thành nhân tử nữa. Chỉ thu gọn được thành $8x^3+50x^2-55x+10$

A B C M N I K
a/ Ta có
\(AB\perp AC\left(gt\right)\Rightarrow AM\perp AC;IN\perp AC\left(gt\right)\) => AM//IN
\(AC\perp AB\left(gt\right)\Rightarrow AN\perp AB;IM\perp AB\left(gt\right)\) => AN//IM
=> AMIN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> AMIN là HCN
b/
Ta co
AM//IN (cmt) =>AB//IK
BK//AI (gt)
=> ABKI là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => BK=AI (cạnh đối hbh)
c/
Xét tg vuông ABC có
\(AI^2=BI.CI\) (Trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow3AI^2=3.BI.CI\) (1)
Xét tg vuông MBI có
\(BM^2=BI^2-MI^2\) (2) (Pitago)
Xét tg vuông NCI có
\(CN^2=CI^2-NI^2\) (3) (Pitago)
Cộng 2 vế của (1) (2) (3) ta có
\(3AI^2+BM^2+CN^2=BI^2+CI^2+3.BI.CI-\left(MI^2+NI^2\right)=\)
\(=\left(BI+CI\right)^2+BI.CI-\left(MI^2+NI^2\right)=\)
\(=BC^2+BI.CI-\left(MI^2+NI^2\right)\) (4)
Ta có
\(BI.CI=AI^2\left(cmt\right)\) (5)
Xét tg vuông AIN có
\(AI^2=AN^2+NI^2\)
Do AMIN là HCN (cnt) => AN=MI
\(\Rightarrow AI^2=MI^2+NI^2\) (6)
Thay (5) và (6) vào (4) ta có
\(3AI^2+BM^2+CN^2=BC^2+AI^2-AI^2\)
\(\Rightarrow BC^2=3AI^2+BM^2+CN^2\left(dpcm\right)\)


O A C D H K I E
a/
Ta có
HA=HO (gt)
\(OA\perp CD\left(gt\right)\) => HC=HD (Trong đường tròn đường kính vuông góc với dây cung thì chia đôi dây cung)
=> OCAD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
Mà \(OA\perp CD\left(gt\right)\)
=> OCAD là hình thoi (Hình bình hành có 2 đường chéo vuôn góc là hình thoi)
b/ Kéo dài AO cắt (O) tại K ta có
\(\widehat{ACK}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông ACK có
\(OA=OK\Rightarrow OC=OA=OK=\dfrac{AK}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà \(OC=AC\) (cạn hình thoi)
\(\Rightarrow OC=AC=OA\) => tg ACO là tg đều \(\Rightarrow\widehat{AOC}=60^o\)
Mà \(\widehat{AOD}=\widehat{AOC}=60^o\) (trong hình thoi mỗi đường chéo là phân giác của 2 góc đối)
\(\Rightarrow\widehat{AOC}+\widehat{AOD}=\widehat{COD}=60^o+60^o=120^o\)
c/
Xét tg vuông COI có
\(\widehat{CIO}=90^o-\widehat{AOC}=90^o-60^o=30^o\)
\(\Rightarrow OC=\dfrac{1}{2}OI\) (trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền
\(\Rightarrow OI=2.OC=2R\)
\(\Rightarrow CI=\sqrt{OI^2-OC^2}\) (Pitago)
\(\Rightarrow CI=\sqrt{4R^2-R^2}=R\sqrt{3}\)
d/
Xét tg COI và tg DOI có
OC=OD=R
OI chung
\(\widehat{AOC}=\widehat{AOD}\) (cmt)
=> tg ACO = tg ADO (c.g.c)\(\Rightarrow\widehat{ODI}=\widehat{OCI}=90^o\) => DI là tiếp tuyến với (O)
e/
Ta có
\(sđ\widehat{COD}=sđcungCD=120^o\) (góc có đỉnh là tâm đường tròn)
\(sđ\widehat{ACD}=\dfrac{1}{2}sđcungCD=60^o\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{ADC}=\dfrac{1}{2}sđcungCD=60^o\) (góc giữa tiếp tuyến và dây cung)
Xét tg ACD có
\(\widehat{CAD}=180^o-\left(\widehat{ACD}+\widehat{ADC}\right)=180^o-\left(60^o+60^o\right)=60^o\)
\(\Rightarrow\widehat{CAD}=\widehat{ACD}=\widehat{ADC}=60^o\) => tg ACD là tg đều
f/
Ta có
\(\widehat{ECD}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow EC\perp CD\)
\(OA\perp CD\left(gt\right)\Rightarrow OI\perp CD\)
=> EC//OI (cùng vuông góc với CD)

Xét tg vuông ABC
\(MB=MC\left(gt\right)\Rightarrow MA=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Xét tg MAC có
MA=MC (cmt) => tg MAC cân tạo M \(\Rightarrow\widehat{MAC}=\widehat{ACB}\) (1)
\(\widehat{ABC}=\widehat{HAC}\) (cùng phụ với \(\widehat{ACB}\) ) (2)
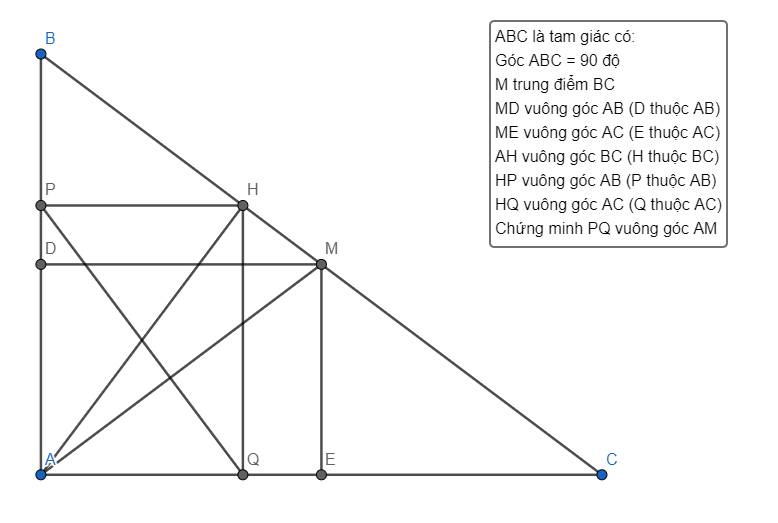
Gọi O là giao của AH và PQ
Xét tứ giác APHQ có
\(AB\perp AC\left(gt\right);HQ\perp AC\left(gt\right)\) => AB//HQ
\(AC\perp AB\left(gt\right);HP\perp AB\left(gt\right)\) => AC//HP
=> APHQ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
Mà \(\widehat{A}=90^o\left(gt\right)\) => APHQ là hình chữ nhật
\(\Rightarrow AH=PQ\) (2 đường chéo HCN băng nhau)
Mà OA=OH; OP= OQ (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> OA=OH=OP=OQ => tg OAQ là tg cân tạo O
\(\Rightarrow\widehat{HAC}=\widehat{AQP}\) (góc ở đáy tg cân) (3)
Từ (2) và (3) \(\Rightarrow\widehat{ABC}=\widehat{AQP}\) (4)
Xét tg vuông ABC có \(\widehat{ABC}+\widehat{ACB}=90^o\) (5)
Từ (1) (4) (5) \(\Rightarrow\widehat{AQP}+\widehat{MAC}=90^o\)
Gọi K là giao của PQ và AM, xét tg AKQ có
\(\widehat{AKQ}=180^o-\left(\widehat{AQP}+\widehat{MAC}\right)=180^o-90^o=90^o\)
\(\Rightarrow PQ\perp AM\left(dpcm\right)\)

Em ơi em đăng câu hỏi thì dùng công thức toán học để viết chữ viết thế này ai hiểu đúng được em?